Related insights
Explore related documents that you might be interested in.
Read Online
Executive Summary
The first few years of primary school are when crucial maths learning happens. Years 1-3 are when students develop the foundational maths skills and understandings that they need for future success. However, many students aren’t as confident about maths as they could be, and national maths achievement is declining.
ERO looked at good practice in the teaching of maths in Years 1-3. We used robust evidence to clarify ‘what good looks like’ for maths teaching in the early years of school, and how teachers can implement these practices in their classrooms. This summary gives an overview of what we learnt.
ERO looked at good practice in maths teaching for Years 1-3
Maths is important. It is the pathway to success across a wide range of learning areas and longer-term life outcomes. High-quality, deliberate maths teaching makes a big difference for students’ confidence and capability in maths, starting in the crucial early years of primary school.
ERO wanted to find out what good practice looks like, for maths teaching in Years 1 to 3. We started with a deep dive into the evidence base, looking at a wide range of national and international research that clarifies what works best for young students. Then we talked to students, teachers, and school leaders from 12 diverse primary schools, to hear how they put these evidence-based maths practices into action.
ERO’s report and guide for teachers share practical strategies for Year 1-3 teachers, to support improvements in this vital area of teaching and learning.
Why we need to focus on improving maths teaching
Our national maths achievement picture is poor
The 2022 National Monitoring Study of Student Achievement (NMSSA) study shows a concerning shift in maths achievement between Year 4 and Year 8, from 82 percent meeting curriculum expectations in Year 4 to less than half (42 percent) of Year 8 students – right as they are about to enter secondary school. Maths results from late primary school and beyond have their roots in the preparation that students receive – or don’t – in their early years at school. Building a strong foundation of early maths skills, concepts, and understandings is crucial to later success.
We also know that student confidence in maths is often lower than in other subjects. It is common to hear both adults and children in say they are ‘bad at maths’, or that maths is ‘only for some people’. The recent Programme for International Student Assessment (PISA) study, which assesses the knowledge and skills of 15-year-old students in mathematics, shows that two thirds of students worry about doing badly in maths, and over half experience anxiety about failing maths.
Achievement results from the 2022 Programme for International Student Assessment (PISA) study are very worrying. These show that the maths skills and knowledge of our 15-year-olds have seen a significant decline over the last 20 years. (See Figure 1.) In 2022, Aotearoa New Zealand’s average mathematics score was above the OECD average, but lower than 2003-2018.
Figure 1: Aotearoa New Zealand and OECD mean mathematics scores, 2003-2022
Error bars on the graph provide a 95% confidence interval for the estimate of the average. The OECD mean shown is based on as many of the 38 countries that have data available. These estimates differ slightly from the OECD reports as they include more countries. Luxembourg did not participate in 2022.
Source: OECD, 2023
PISA’s 2022 study also shows:
- the difference between our highest- and lowest- performers has widened and shifted down, and is among the widest in the OECD
- the proportion of “low” performers has increased since 2018 and almost doubled since 2003 (29 percent compared to 15 percent)
- the proportion of “high” performers (those who score Level 5 or above) has halved since 2003
- there is a higher difference between the scores of the lowest and highest advantaged students in New Zealand than the OECD average
- boys score higher than girls, on average, and a higher proportion of boys are high performers
- anxiety about maths has increased, and is higher than the OECD average, with girls reporting significantly higher anxiety than boys
- our students report a relatively negative learning environment compared to most other countries.
Not all teachers are confident about teaching maths
ERO surveyed new primary teachers in 2023, finding that nearly a quarter (24 percent) had felt ‘unprepared’ in their maths content knowledge when they first started in their role. While national studies show that most primary teachers enjoy teaching maths and agree it is important, teachers in the junior school are less confident about teaching all strands of mathematics than their senior peers (comparing Year 4 and Year 8 teachers). Teachers are not as well set up as they could be for the deliberate, structured approach to maths teaching that the evidence tells us makes the difference.
Maths in early primary school matters
Maths achievement in the primary years is linked to later success across a range of life outcomes, like higher education achievement, better jobs, better income, and social mobility. Maths results have even been shown to impact on national economies.
In the early years of primary school, teachers have the opportunity to set the scene for their young maths students through purposeful strategies and explicit instruction. It is in these early years that students learn about the building blocks of all future maths learning, and develop their understanding of how capable they are as maths students. Maths learning builds on itself and gets more complex over a student’s time in school, so getting the foundation right is really important. Any misunderstandings, shortcuts, poor self-belief, or lack of engagement in these early years sets a poor foundation for years to come.
To make this happen, teachers need to ensure that all students benefit from high-quality maths experiences every day. When maths is a consistent and engaging feature of the daily classroom programme, students have lots of opportunities to make connections, cement new learning, think and talk in maths terms, and explore maths ideas. Purposeful and evidence-based maths practices are the key to more confident maths students in the future.
What are the main things to know about good practice in maths in Years 1-3?
ERO drew on robust global and local evidence and experts to find out what really makes a difference for Year 1-3 maths learning. We found that there are two key enablers, and nine key areas of teacher practice, that have the most powerful impact on learner outcomes.
There are two enablers for great maths teaching practice
These are the enablers that need to be in place before teachers can do their best maths teaching.
Enabler 1: Teacher knowledge
Teachers need to be confident in their own maths knowledge and skills, to be ready to teach them to students. They also need to understand what works best for young students: the specific teaching strategies that are most effective in setting students up for this crucial time in their maths journey. This includes being clear about how to structure their teaching to develop important maths understandings over time, while avoiding misunderstandings or shortcuts which negatively impact on later learning.
Enabler 2: School culture and a whole school curriculum
Teachers’ school settings can promote good maths practice through a clear, shared understanding of quality maths teaching. This involves clearly setting out what maths teaching and maths progress looks like in a documented, structured whole school curriculum, and by supporting teacher understanding with great learning and collaboration opportunities. It’s useful when schools have an embedded culture of being open to learning, sharing, and continually improving.
There are nine key areas of teacher practice
The national and international research evidence base shows that there are nine key areas of practice that make a real difference for young maths students.
|
Practice area 1 |
Teachers use their understanding of assessment and how students learn maths to ensure they all progress |
|
Practice area 2 |
Teachers use quality teaching practice in maths |
|
Practice area 3 |
Teachers provide dedicated maths time every day so all students engage meaningfully in learning |
|
Practice area 4 |
Teachers notice when students require extra support for learning and provide effective targeted teaching |
|
Practice area 5 |
Teachers use tools and representations to express mathematical concepts |
|
Practice area 6 |
The classroom learning environment encourages mathematical thinking, collaboration, and the enjoyment of maths |
|
Practice area 7 |
Teachers make the most of moments throughout the day to highlight and use maths |
|
Practice area 8 |
Maths classes reflect the cultures of their students and families/ whānau |
|
Practice area 9 |
Teachers work in partnership with families / whānau to support maths learning. |
What does good teacher practice look like, across the nine key areas of practice?
ERO reviewed the international evidence base to establish a robust set of the highest-impact teacher practices, that the evidence shows make a real difference for maths learning. We then worked with schools and experts to find out how these practices can be applied effectively in an Aotearoa New Zealand context. Below is a summary of the nine key areas of practice, why they matter, and how they can look when teachers put them into action.
Practice area 1: Teachers use their understanding of assessment and how students learn maths to ensure they all progress
This practice area is about teachers using their knowledge of students and about how maths concepts connect and build on each other, to line up learning experiences in a deliberate way.
Key teacher practices are:
1 a) teachers determine what students bring to their learning, and build on what they already know
1 b) teachers actively notice, recognise, and respond to students’ progress as they engage in maths
1 c) teachers use assessment and progressions to plan for, document and monitor students’ progress.
Why this is important
It is important that teachers gain an in-depth awareness of students’ understanding, so that they can respond in a timely and effective way to move them forward. Assessment helps teachers to set up expectations and goals for students, and plan purposeful learning steps which they can monitor to inform their decisions to move on. Assessing students’ understanding and knowledge also helps teachers adapt their practice and understand how effective it is in promoting the learning and progress of their students.
What this can look like in real life
Teachers work with leaders to align their views on expected progress from Year 1. These are used to develop a schoolwide document of expectations for maths progression. This provides teachers with “the backbone of the curriculum plan, and they all know what they are doing, and how to adjust their teaching to the students.” (School leader)
Practice area 2: Teachers use quality teaching practice in maths
This practice area is about ensuring effective teaching practices form the foundation for maths teaching practice. This means using deliberate, intentional teaching and organisational strategies that support students to focus, draw out their ideas, and support their progress. Teachers will draw on good questioning skills and use timely, specific, and actionable feedback. They recognise when to support or extend students, when to move on to new learning, and when to spend longer on an area to consolidate learning for all students in their class.
Key teacher practices are:
2 a) teachers provide scaffolding for students in maths
2 b) teachers use explicit teaching in maths
2 c) teachers use flexible grouping in maths
2 d) teachers provide a range of cognitive and metacognitive strategies in maths.
Why this is important
Teachers are not able to capably implement good maths-specific practices without knowledge of key teaching practices that work. Teachers who demonstrate good quality teaching skills in other learning areas are well on the way to being effective teachers of maths.
What this can look like in real life
A teacher works with a small group in Year 1 to scaffold their learning about ordering numbers. She prompts them about their prior learning, “Remember we have been learning about the word ‘after’ – like ‘after school’, ‘after playtime,’ then we talked about lining up.” The teacher arranges the five students in a line and asks them to turn and identify, “Who’s after you? Who’s before you?” The teacher then talks about how this works with numbers too. She uses a cut-out arrow to point to a number in a sequence to 10 written on the tabletop. She then asks students to point to numbers that are directly ‘before’, and ‘after’. Students then write the number themselves on the table with whiteboard pens. They each use number strips and put their finger on a number, then write the number that comes before, and after. They then continue this exercise on paper.
Practice area 3: Teachers provide dedicated maths time every day so all students engage meaningfully in learning
This practice area is about providing daily opportunities to learn and practise maths. Daily maths should be timetabled, purposeful, and sequenced in a way that builds on existing knowledge and prepares students for further complexity. Within the time that is dedicated to maths, every effort should be made to maximise the time spent learning.
Key teacher practices are:
3 a) teachers support students to learn, practise, create, and use maths daily
3 b) teachers show students how to use maths procedures and skills accurately, efficiently, and flexibly
3 c) teachers prompt students to talk about their maths ideas
3 d) teachers provide cognitively challenging maths activities.
Why this is important
Focused daily maths time is needed for students to continually develop their foundational maths skills and knowledge. Studies show that students achieve better in maths when they have daily exposure to maths instruction, time to practise, and opportunities for application and critical thinking. At this early stage of their maths journey, it is important students have sufficient time to interact with and familiarise with maths concepts. This involves providing students with learning experiences at a pace that challenges them and supports their continued progress.
What this can look like in real life
Leaders and teachers in one school have reviewed their approach to maths across the junior school. They put strategies in place to ensure there was a consistent approach to prioritising and implementing maths. This includes a schoolwide discussion on maths topics, followed by planning sessions in the syndicate, with a strong focus on unpacking maths concepts.
To strengthen their focus on maths, teachers at one school have established a consistent ‘maths time’ at the start of each day – the time that they had noticed students are most engaged. All teachers work through agreed content, and undertake assessments at the same time at the end of a unit. In their review, they had also recognised that the areas of weakest performance (e.g. fractions) were taught later in the year. To remedy this, fractions was brought to the start of the year, for more focus and stronger effort.
Practice area 4: Teachers notice when students require extra support for learning and provide effective targeted teaching
This practice area is about paying attention to students who may demonstrate a lack of engagement, motivation, or success in maths. Teachers recognise when to support or extend a student, when to move on to new learning, or when to spend longer on an area to consolidate learning for individual students. Teachers need to understand any barriers to learning and find effective ways to ensure all students make progress.
Key teacher practices are:
4 a) teachers identify and monitor students who need additional support
4 b) teachers partner with others and are supported to implement targeted approaches
4 c) teachers support students with identified needs to access and engage through planned and targeted interventions
4 d) teachers extend competent maths students through adding challenge and complexity.
Why this is important
Foundational maths concepts and attitudes that are learnt during the first few years of school set students up for success – or struggle – for the rest of their maths journey, even into adulthood. Early experiences of maths leave lasting impressions and impact on students’ ongoing achievement. It is essential teachers are alert to early signs of difficulty or disengagement, and act on these promptly.
What this can look like in real life
At one school, teacher aides who are trained in a targeted maths intervention run a 15-minute structured programme during the class maths lesson. These sessions are designed to attend to the specific areas of maths learning that individual students require support with, and content is clearly linked to the content of the main session. Students in the intervention group join their peers for the majority of daily maths time.
Practice area 5: Teachers use tools and representations to express mathematical concepts
This practice area is about teachers intentionally using a range of materials, specialised equipment, diagrams, and symbols as they introduce or reinforce maths concepts. They model how to use and apply tools and representations, supporting students to understand and express ideas related to the concepts being taught.
Key teacher practices are:
5 a) teachers plan how to use tools and representations, based on a clear rationale
5 b) teachers make clear links between maths concepts and tools and representations
5 c) teachers encourage students to use or adapt tools and representations to express their maths ideas.
Why this is important
Mathematics is highly abstract, and students need good support to be able to make sense of these abstract ideas. Providing deliberate strategies for making these links is a key part of the teacher’s role. Evidence shows that tools and representations help young students to build their mental models of key maths concepts and processes, by making connections to the physical (‘real’) world.
What this can look like in real life
A teacher plans a lesson for a Year 2 group to focus on dividing 24 counters into four groups – but ensures she also has fraction strips, an abacus, and multiplication arrays handy. During the lesson, this preparation helps her to reinforce the learning for some students by modelling connections to fractions, and repeated addition as well as multiplication and division.
Practice area 6: The classroom learning environment encourages mathematical thinking, collaboration, and the enjoyment of maths
This practice area involves physical set-up (the classroom itself) as well as emotional and behavioural set-up (behaviours, values, and rules). For example, teachers might arrange displays and seating to promote participation, talk explicitly about rules and expectations for respectful maths debate, and provide plenty of opportunities for students to talk about maths with their peers, confidently take part in discussions, and record and communicate their ideas.
Key teacher practices are:
6 a) teachers learn about students and their relationship with maths
6 b) teachers build a classroom culture that encourages engagement in maths learning
6 c) teachers organise the classroom environment to encourage engagement in maths learning.
Why this is important
Classroom environments can encourage – or discourage – engagement and learning, setting the scene for each maths lesson. This is true of both through the physical environment (how the classroom is arranged) and the emotional environment (whether learning about and discussing maths feels safe and inviting).
With targeted actions, teachers can create a classroom culture where all students feel confident to contribute ideas, participate in maths talk, and express their ideas, learn from their mistakes, try different maths methods, and problem-solve with and learn from their peers. The way teachers encourage and respond to students, and how classmates work with one another, is crucial. Good rules and expectations can help with this.
What this can look like in real life
A teacher purposefully roams the classroom and observes maths group tasks, with particular attention paid to whether some students are doing more of the work while others are passive. The teacher intervenes to remind the group about agreed practices for maths group work, for example, ‘Everyone shares ideas.’
Practice area 7: Teachers make the most of moments throughout the day to highlight and use maths
This practice area is about teachers strengthening students’ understandings of maths by highlighting all the ways that maths ideas are relevant within their world – not only in maths lessons. This can occur in planned or spontaneous ways, within the range of everyday activities that take place in a school day, including routines, play, and other curriculum areas.
Key teacher practices are:
7 a) teachers plan how maths ideas are incorporated into a range of activities
7 b) teachers make links to maths when teaching other curriculum areas
7 c) teachers find spontaneous ways to bring maths concepts into play and routine tasks.
Why this is important
Regularly highlighting maths concepts in contexts that aren’t maths sessions helps students to see the ‘hidden maths’ that is all around, which can ignite their interest, curiosity, and maths learning. When maths keeps popping up in everyday activities, like routines and other subject areas, this demonstrates the relevance and application of maths throughout students’ lives. This practice also provides additional, meaningful opportunities to practise maths skills.
What this can look like in real life
During cross-country training, students receive a bean for every lap they run. After training, they work together to update a class bar graph that shows their number of laps.
Practice area 8: Maths classes reflect the cultures of their students and whānau
This practice area is about reflecting the cultures of students through the choice of tasks, the scenarios used for problem solving, or the materials used in teaching and learning.
Key teacher practices are:
8 a) teachers demonstrate and help all students make connections between maths and te ao Māori
8 b) teachers ensure maths tasks include contexts, content, or approaches that are culturally relevant to students
8 c) teachers use the classroom environment to promote interest in maths through cultural contexts, symbols, materials, and artefacts.
Why this is important
Students find maths more relevant and interesting when maths tasks are clearly linked to their culture, language, and home experiences. As well as supporting interest and engagement, using familiar contexts also reduces the ‘cognitive load’ for students: all their focus can be on understanding the maths problem – rather than also trying to make sense of an unfamiliar context.
What this can look like in real life
In a class with a high proportion of Pacific students, the context of White Sunday is used for setting maths word problems, for example: ‘Nearly all of Sione’s aiga attended White Sunday at his church last week. Here are the different people in his family (using photographs or diagrams). How many altogether? Half of the 150 people at the church were children – how many children were there?’
Practice area 9: Teachers work in partnership with families / whānau to support maths learning
This practice area is about teachers working closely with families to learn about maths practices within home contexts, showing or talking with whānau about what maths looks like in their child’s classroom, and offering ideas and resources so that they can support their child with maths in their home and community.
Key teacher practices are:
9 a) teachers talk about maths learning with families/whānau
9 b) teachers provide maths information and resources to families/whānau to reinforce what is being learnt in the classroom.
Why this is important
It’s important for young students to see themselves as capable maths students, experience maths concepts and ideas in a range of contexts, and have opportunities to practise and use maths in ways that feel relevant to them. Strong home-school partnerships help with all of these. Teachers can work with families/whānau to ensure that students benefit from shared, positive messages about their maths capability and the value of maths learning, as well as reinforce and embed the learning that happens in the classroom.
What this can look like in real life
Some schools hold open days for families/whānau to attend classes during maths time. These sessions purposefully demonstrate how teachers and students use equipment, how students work together, the role of games as part of a maths teaching session, and how teachers provide explicit teaching. This supports families to understand what maths teaching and learning looks like, and how ‘maths talk’ can easily be incorporated at home.
These nine key areas work as a set of effective practices. When teachers develop proficiency in each of these areas, supported by the enablers of good teacher knowledge and effective school conditions, the evidence shows that students benefit. This means that Year 1-3 teachers have the opportunity to set learners up with a crucial foundation for positive learning and life outcomes well beyond these early years.
What next?
Maths teaching and learning needs improvement. Our achievement picture isn’t strong, and not all teachers are confident about teaching maths. Worrying maths results from late primary school and beyond have their roots in the preparation that students receive – or don’t – in their early years at school. Now is the time to support teachers with deliberate, practical strategies that make a difference.
Great maths teaching starts with teachers valuing maths. When maths is prioritised, this is visible through teacher actions like dedicated daily maths time, weaving maths learning throughout other curriculum areas, purposeful use of maths talk, linking students’ interests and cultures back to maths ideas, and making great tools and materials available and well understood. This all starts with clear messages from teachers: that maths is important, maths connects to their world, maths is fun and interesting, and maths is for everyone.
We appreciate the work of all those who supported this research, particularly the teachers, school leaders, and students who shared with us. Their experiences and insights are at the heart of what we have learnt.
The first few years of primary school are when crucial maths learning happens. Years 1-3 are when students develop the foundational maths skills and understandings that they need for future success. However, many students aren’t as confident about maths as they could be, and national maths achievement is declining.
ERO looked at good practice in the teaching of maths in Years 1-3. We used robust evidence to clarify ‘what good looks like’ for maths teaching in the early years of school, and how teachers can implement these practices in their classrooms. This summary gives an overview of what we learnt.
ERO looked at good practice in maths teaching for Years 1-3
Maths is important. It is the pathway to success across a wide range of learning areas and longer-term life outcomes. High-quality, deliberate maths teaching makes a big difference for students’ confidence and capability in maths, starting in the crucial early years of primary school.
ERO wanted to find out what good practice looks like, for maths teaching in Years 1 to 3. We started with a deep dive into the evidence base, looking at a wide range of national and international research that clarifies what works best for young students. Then we talked to students, teachers, and school leaders from 12 diverse primary schools, to hear how they put these evidence-based maths practices into action.
ERO’s report and guide for teachers share practical strategies for Year 1-3 teachers, to support improvements in this vital area of teaching and learning.
Why we need to focus on improving maths teaching
Our national maths achievement picture is poor
The 2022 National Monitoring Study of Student Achievement (NMSSA) study shows a concerning shift in maths achievement between Year 4 and Year 8, from 82 percent meeting curriculum expectations in Year 4 to less than half (42 percent) of Year 8 students – right as they are about to enter secondary school. Maths results from late primary school and beyond have their roots in the preparation that students receive – or don’t – in their early years at school. Building a strong foundation of early maths skills, concepts, and understandings is crucial to later success.
We also know that student confidence in maths is often lower than in other subjects. It is common to hear both adults and children in say they are ‘bad at maths’, or that maths is ‘only for some people’. The recent Programme for International Student Assessment (PISA) study, which assesses the knowledge and skills of 15-year-old students in mathematics, shows that two thirds of students worry about doing badly in maths, and over half experience anxiety about failing maths.
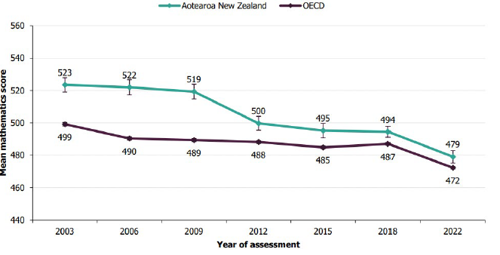
Achievement results from the 2022 Programme for International Student Assessment (PISA) study are very worrying. These show that the maths skills and knowledge of our 15-year-olds have seen a significant decline over the last 20 years. (See Figure 1.) In 2022, Aotearoa New Zealand’s average mathematics score was above the OECD average, but lower than 2003-2018.
Figure 1: Aotearoa New Zealand and OECD mean mathematics scores, 2003-2022

Error bars on the graph provide a 95% confidence interval for the estimate of the average. The OECD mean shown is based on as many of the 38 countries that have data available. These estimates differ slightly from the OECD reports as they include more countries. Luxembourg did not participate in 2022.
Source: OECD, 2023
PISA’s 2022 study also shows:
- the difference between our highest- and lowest- performers has widened and shifted down, and is among the widest in the OECD
- the proportion of “low” performers has increased since 2018 and almost doubled since 2003 (29 percent compared to 15 percent)
- the proportion of “high” performers (those who score Level 5 or above) has halved since 2003
- there is a higher difference between the scores of the lowest and highest advantaged students in New Zealand than the OECD average
- boys score higher than girls, on average, and a higher proportion of boys are high performers
- anxiety about maths has increased, and is higher than the OECD average, with girls reporting significantly higher anxiety than boys
- our students report a relatively negative learning environment compared to most other countries.
Not all teachers are confident about teaching maths
ERO surveyed new primary teachers in 2023, finding that nearly a quarter (24 percent) had felt ‘unprepared’ in their maths content knowledge when they first started in their role. While national studies show that most primary teachers enjoy teaching maths and agree it is important, teachers in the junior school are less confident about teaching all strands of mathematics than their senior peers (comparing Year 4 and Year 8 teachers). Teachers are not as well set up as they could be for the deliberate, structured approach to maths teaching that the evidence tells us makes the difference.
Maths in early primary school matters
Maths achievement in the primary years is linked to later success across a range of life outcomes, like higher education achievement, better jobs, better income, and social mobility. Maths results have even been shown to impact on national economies.
In the early years of primary school, teachers have the opportunity to set the scene for their young maths students through purposeful strategies and explicit instruction. It is in these early years that students learn about the building blocks of all future maths learning, and develop their understanding of how capable they are as maths students. Maths learning builds on itself and gets more complex over a student’s time in school, so getting the foundation right is really important. Any misunderstandings, shortcuts, poor self-belief, or lack of engagement in these early years sets a poor foundation for years to come.
To make this happen, teachers need to ensure that all students benefit from high-quality maths experiences every day. When maths is a consistent and engaging feature of the daily classroom programme, students have lots of opportunities to make connections, cement new learning, think and talk in maths terms, and explore maths ideas. Purposeful and evidence-based maths practices are the key to more confident maths students in the future.
What are the main things to know about good practice in maths in Years 1-3?
ERO drew on robust global and local evidence and experts to find out what really makes a difference for Year 1-3 maths learning. We found that there are two key enablers, and nine key areas of teacher practice, that have the most powerful impact on learner outcomes.
There are two enablers for great maths teaching practice
These are the enablers that need to be in place before teachers can do their best maths teaching.
Enabler 1: Teacher knowledge
Teachers need to be confident in their own maths knowledge and skills, to be ready to teach them to students. They also need to understand what works best for young students: the specific teaching strategies that are most effective in setting students up for this crucial time in their maths journey. This includes being clear about how to structure their teaching to develop important maths understandings over time, while avoiding misunderstandings or shortcuts which negatively impact on later learning.
Enabler 2: School culture and a whole school curriculum
Teachers’ school settings can promote good maths practice through a clear, shared understanding of quality maths teaching. This involves clearly setting out what maths teaching and maths progress looks like in a documented, structured whole school curriculum, and by supporting teacher understanding with great learning and collaboration opportunities. It’s useful when schools have an embedded culture of being open to learning, sharing, and continually improving.
There are nine key areas of teacher practice
The national and international research evidence base shows that there are nine key areas of practice that make a real difference for young maths students.
|
Practice area 1 |
Teachers use their understanding of assessment and how students learn maths to ensure they all progress |
|
Practice area 2 |
Teachers use quality teaching practice in maths |
|
Practice area 3 |
Teachers provide dedicated maths time every day so all students engage meaningfully in learning |
|
Practice area 4 |
Teachers notice when students require extra support for learning and provide effective targeted teaching |
|
Practice area 5 |
Teachers use tools and representations to express mathematical concepts |
|
Practice area 6 |
The classroom learning environment encourages mathematical thinking, collaboration, and the enjoyment of maths |
|
Practice area 7 |
Teachers make the most of moments throughout the day to highlight and use maths |
|
Practice area 8 |
Maths classes reflect the cultures of their students and families/ whānau |
|
Practice area 9 |
Teachers work in partnership with families / whānau to support maths learning. |
What does good teacher practice look like, across the nine key areas of practice?
ERO reviewed the international evidence base to establish a robust set of the highest-impact teacher practices, that the evidence shows make a real difference for maths learning. We then worked with schools and experts to find out how these practices can be applied effectively in an Aotearoa New Zealand context. Below is a summary of the nine key areas of practice, why they matter, and how they can look when teachers put them into action.
Practice area 1: Teachers use their understanding of assessment and how students learn maths to ensure they all progress
This practice area is about teachers using their knowledge of students and about how maths concepts connect and build on each other, to line up learning experiences in a deliberate way.
Key teacher practices are:
1 a) teachers determine what students bring to their learning, and build on what they already know
1 b) teachers actively notice, recognise, and respond to students’ progress as they engage in maths
1 c) teachers use assessment and progressions to plan for, document and monitor students’ progress.
Why this is important
It is important that teachers gain an in-depth awareness of students’ understanding, so that they can respond in a timely and effective way to move them forward. Assessment helps teachers to set up expectations and goals for students, and plan purposeful learning steps which they can monitor to inform their decisions to move on. Assessing students’ understanding and knowledge also helps teachers adapt their practice and understand how effective it is in promoting the learning and progress of their students.
What this can look like in real life
Teachers work with leaders to align their views on expected progress from Year 1. These are used to develop a schoolwide document of expectations for maths progression. This provides teachers with “the backbone of the curriculum plan, and they all know what they are doing, and how to adjust their teaching to the students.” (School leader)
Practice area 2: Teachers use quality teaching practice in maths
This practice area is about ensuring effective teaching practices form the foundation for maths teaching practice. This means using deliberate, intentional teaching and organisational strategies that support students to focus, draw out their ideas, and support their progress. Teachers will draw on good questioning skills and use timely, specific, and actionable feedback. They recognise when to support or extend students, when to move on to new learning, and when to spend longer on an area to consolidate learning for all students in their class.
Key teacher practices are:
2 a) teachers provide scaffolding for students in maths
2 b) teachers use explicit teaching in maths
2 c) teachers use flexible grouping in maths
2 d) teachers provide a range of cognitive and metacognitive strategies in maths.
Why this is important
Teachers are not able to capably implement good maths-specific practices without knowledge of key teaching practices that work. Teachers who demonstrate good quality teaching skills in other learning areas are well on the way to being effective teachers of maths.
What this can look like in real life
A teacher works with a small group in Year 1 to scaffold their learning about ordering numbers. She prompts them about their prior learning, “Remember we have been learning about the word ‘after’ – like ‘after school’, ‘after playtime,’ then we talked about lining up.” The teacher arranges the five students in a line and asks them to turn and identify, “Who’s after you? Who’s before you?” The teacher then talks about how this works with numbers too. She uses a cut-out arrow to point to a number in a sequence to 10 written on the tabletop. She then asks students to point to numbers that are directly ‘before’, and ‘after’. Students then write the number themselves on the table with whiteboard pens. They each use number strips and put their finger on a number, then write the number that comes before, and after. They then continue this exercise on paper.
Practice area 3: Teachers provide dedicated maths time every day so all students engage meaningfully in learning
This practice area is about providing daily opportunities to learn and practise maths. Daily maths should be timetabled, purposeful, and sequenced in a way that builds on existing knowledge and prepares students for further complexity. Within the time that is dedicated to maths, every effort should be made to maximise the time spent learning.
Key teacher practices are:
3 a) teachers support students to learn, practise, create, and use maths daily
3 b) teachers show students how to use maths procedures and skills accurately, efficiently, and flexibly
3 c) teachers prompt students to talk about their maths ideas
3 d) teachers provide cognitively challenging maths activities.
Why this is important
Focused daily maths time is needed for students to continually develop their foundational maths skills and knowledge. Studies show that students achieve better in maths when they have daily exposure to maths instruction, time to practise, and opportunities for application and critical thinking. At this early stage of their maths journey, it is important students have sufficient time to interact with and familiarise with maths concepts. This involves providing students with learning experiences at a pace that challenges them and supports their continued progress.
What this can look like in real life
Leaders and teachers in one school have reviewed their approach to maths across the junior school. They put strategies in place to ensure there was a consistent approach to prioritising and implementing maths. This includes a schoolwide discussion on maths topics, followed by planning sessions in the syndicate, with a strong focus on unpacking maths concepts.
To strengthen their focus on maths, teachers at one school have established a consistent ‘maths time’ at the start of each day – the time that they had noticed students are most engaged. All teachers work through agreed content, and undertake assessments at the same time at the end of a unit. In their review, they had also recognised that the areas of weakest performance (e.g. fractions) were taught later in the year. To remedy this, fractions was brought to the start of the year, for more focus and stronger effort.
Practice area 4: Teachers notice when students require extra support for learning and provide effective targeted teaching
This practice area is about paying attention to students who may demonstrate a lack of engagement, motivation, or success in maths. Teachers recognise when to support or extend a student, when to move on to new learning, or when to spend longer on an area to consolidate learning for individual students. Teachers need to understand any barriers to learning and find effective ways to ensure all students make progress.
Key teacher practices are:
4 a) teachers identify and monitor students who need additional support
4 b) teachers partner with others and are supported to implement targeted approaches
4 c) teachers support students with identified needs to access and engage through planned and targeted interventions
4 d) teachers extend competent maths students through adding challenge and complexity.
Why this is important
Foundational maths concepts and attitudes that are learnt during the first few years of school set students up for success – or struggle – for the rest of their maths journey, even into adulthood. Early experiences of maths leave lasting impressions and impact on students’ ongoing achievement. It is essential teachers are alert to early signs of difficulty or disengagement, and act on these promptly.
What this can look like in real life
At one school, teacher aides who are trained in a targeted maths intervention run a 15-minute structured programme during the class maths lesson. These sessions are designed to attend to the specific areas of maths learning that individual students require support with, and content is clearly linked to the content of the main session. Students in the intervention group join their peers for the majority of daily maths time.
Practice area 5: Teachers use tools and representations to express mathematical concepts
This practice area is about teachers intentionally using a range of materials, specialised equipment, diagrams, and symbols as they introduce or reinforce maths concepts. They model how to use and apply tools and representations, supporting students to understand and express ideas related to the concepts being taught.
Key teacher practices are:
5 a) teachers plan how to use tools and representations, based on a clear rationale
5 b) teachers make clear links between maths concepts and tools and representations
5 c) teachers encourage students to use or adapt tools and representations to express their maths ideas.
Why this is important
Mathematics is highly abstract, and students need good support to be able to make sense of these abstract ideas. Providing deliberate strategies for making these links is a key part of the teacher’s role. Evidence shows that tools and representations help young students to build their mental models of key maths concepts and processes, by making connections to the physical (‘real’) world.
What this can look like in real life
A teacher plans a lesson for a Year 2 group to focus on dividing 24 counters into four groups – but ensures she also has fraction strips, an abacus, and multiplication arrays handy. During the lesson, this preparation helps her to reinforce the learning for some students by modelling connections to fractions, and repeated addition as well as multiplication and division.
Practice area 6: The classroom learning environment encourages mathematical thinking, collaboration, and the enjoyment of maths
This practice area involves physical set-up (the classroom itself) as well as emotional and behavioural set-up (behaviours, values, and rules). For example, teachers might arrange displays and seating to promote participation, talk explicitly about rules and expectations for respectful maths debate, and provide plenty of opportunities for students to talk about maths with their peers, confidently take part in discussions, and record and communicate their ideas.
Key teacher practices are:
6 a) teachers learn about students and their relationship with maths
6 b) teachers build a classroom culture that encourages engagement in maths learning
6 c) teachers organise the classroom environment to encourage engagement in maths learning.
Why this is important
Classroom environments can encourage – or discourage – engagement and learning, setting the scene for each maths lesson. This is true of both through the physical environment (how the classroom is arranged) and the emotional environment (whether learning about and discussing maths feels safe and inviting).
With targeted actions, teachers can create a classroom culture where all students feel confident to contribute ideas, participate in maths talk, and express their ideas, learn from their mistakes, try different maths methods, and problem-solve with and learn from their peers. The way teachers encourage and respond to students, and how classmates work with one another, is crucial. Good rules and expectations can help with this.
What this can look like in real life
A teacher purposefully roams the classroom and observes maths group tasks, with particular attention paid to whether some students are doing more of the work while others are passive. The teacher intervenes to remind the group about agreed practices for maths group work, for example, ‘Everyone shares ideas.’
Practice area 7: Teachers make the most of moments throughout the day to highlight and use maths
This practice area is about teachers strengthening students’ understandings of maths by highlighting all the ways that maths ideas are relevant within their world – not only in maths lessons. This can occur in planned or spontaneous ways, within the range of everyday activities that take place in a school day, including routines, play, and other curriculum areas.
Key teacher practices are:
7 a) teachers plan how maths ideas are incorporated into a range of activities
7 b) teachers make links to maths when teaching other curriculum areas
7 c) teachers find spontaneous ways to bring maths concepts into play and routine tasks.
Why this is important
Regularly highlighting maths concepts in contexts that aren’t maths sessions helps students to see the ‘hidden maths’ that is all around, which can ignite their interest, curiosity, and maths learning. When maths keeps popping up in everyday activities, like routines and other subject areas, this demonstrates the relevance and application of maths throughout students’ lives. This practice also provides additional, meaningful opportunities to practise maths skills.
What this can look like in real life
During cross-country training, students receive a bean for every lap they run. After training, they work together to update a class bar graph that shows their number of laps.
Practice area 8: Maths classes reflect the cultures of their students and whānau
This practice area is about reflecting the cultures of students through the choice of tasks, the scenarios used for problem solving, or the materials used in teaching and learning.
Key teacher practices are:
8 a) teachers demonstrate and help all students make connections between maths and te ao Māori
8 b) teachers ensure maths tasks include contexts, content, or approaches that are culturally relevant to students
8 c) teachers use the classroom environment to promote interest in maths through cultural contexts, symbols, materials, and artefacts.
Why this is important
Students find maths more relevant and interesting when maths tasks are clearly linked to their culture, language, and home experiences. As well as supporting interest and engagement, using familiar contexts also reduces the ‘cognitive load’ for students: all their focus can be on understanding the maths problem – rather than also trying to make sense of an unfamiliar context.
What this can look like in real life
In a class with a high proportion of Pacific students, the context of White Sunday is used for setting maths word problems, for example: ‘Nearly all of Sione’s aiga attended White Sunday at his church last week. Here are the different people in his family (using photographs or diagrams). How many altogether? Half of the 150 people at the church were children – how many children were there?’
Practice area 9: Teachers work in partnership with families / whānau to support maths learning
This practice area is about teachers working closely with families to learn about maths practices within home contexts, showing or talking with whānau about what maths looks like in their child’s classroom, and offering ideas and resources so that they can support their child with maths in their home and community.
Key teacher practices are:
9 a) teachers talk about maths learning with families/whānau
9 b) teachers provide maths information and resources to families/whānau to reinforce what is being learnt in the classroom.
Why this is important
It’s important for young students to see themselves as capable maths students, experience maths concepts and ideas in a range of contexts, and have opportunities to practise and use maths in ways that feel relevant to them. Strong home-school partnerships help with all of these. Teachers can work with families/whānau to ensure that students benefit from shared, positive messages about their maths capability and the value of maths learning, as well as reinforce and embed the learning that happens in the classroom.
What this can look like in real life
Some schools hold open days for families/whānau to attend classes during maths time. These sessions purposefully demonstrate how teachers and students use equipment, how students work together, the role of games as part of a maths teaching session, and how teachers provide explicit teaching. This supports families to understand what maths teaching and learning looks like, and how ‘maths talk’ can easily be incorporated at home.
These nine key areas work as a set of effective practices. When teachers develop proficiency in each of these areas, supported by the enablers of good teacher knowledge and effective school conditions, the evidence shows that students benefit. This means that Year 1-3 teachers have the opportunity to set learners up with a crucial foundation for positive learning and life outcomes well beyond these early years.
What next?
Maths teaching and learning needs improvement. Our achievement picture isn’t strong, and not all teachers are confident about teaching maths. Worrying maths results from late primary school and beyond have their roots in the preparation that students receive – or don’t – in their early years at school. Now is the time to support teachers with deliberate, practical strategies that make a difference.
Great maths teaching starts with teachers valuing maths. When maths is prioritised, this is visible through teacher actions like dedicated daily maths time, weaving maths learning throughout other curriculum areas, purposeful use of maths talk, linking students’ interests and cultures back to maths ideas, and making great tools and materials available and well understood. This all starts with clear messages from teachers: that maths is important, maths connects to their world, maths is fun and interesting, and maths is for everyone.
We appreciate the work of all those who supported this research, particularly the teachers, school leaders, and students who shared with us. Their experiences and insights are at the heart of what we have learnt.
About this report
This report is for teachers of Years 1 to 3. It draws on research and real-life stories and strategies to shine a light on the key ways that teachers can most effectively teach maths to students in the first years of primary school.
Why we did this research
Maths is important – and not just in the classroom. It helps us understand our world. Mathematical knowledge is a building block of important life skills like problem solving, communication, and creative thinking. However, student and teacher confidence in maths is often lower than in other subjects.(1) It is common to hear both adults and children say they are ‘bad at maths’, or that maths is ‘only for some people’.(2)
It doesn’t have to be like this. Confidence and capabilIty in maths can be developed. The early years of primary school are when students develop their key maths skills and understandings. The experiences, attitudes, and expectations formed at this time greatly influence future success in maths.
The quality of maths teaching makes a big difference for students’ confidence and capability, particularly in the early years of primary school. In Years 1-3, students are forming understandings of crucial maths concepts that will set them up for future learning and educational success. This research and report share practical strategies for quality maths teaching in the early primary years, and shines a light on good practice. It is the aim of this research to lift teachers’ confidence and capability in this pivotal area of their practice. With improvements to maths teaching, all students can be supported to enjoy, find success, and benefit from maths.
“While most New Zealanders likely consider maths knowledge and skills important for our economy and valuable in broader society, many kaiako, teachers and students have encountered views like ‘I was never any good at maths’, or ‘I always hated maths’, or ‘What’s the point of maths?’. These societal perceptions can have a profound impact on maths learning.” – Ministry of Education, 2023. (3)
Maths knowledge has real-life impacts
We use maths every day, all our lives. It’s through maths that we pay for groceries, cook and bake, build houses, read a map, fly planes, split a dinner bill, knit a jumper, convert money when we’re overseas, create special effects for movies, make important life decisions, and save up for our first car. It is also an important part of understanding and interpreting what is happening in our world.
Students develop valuable skills like creative problem solving and logical reasoning through using mathematical processes, ideas, and concepts.(4) Maths learning helps people to view information critically, and drives learning success in areas like science, technology, economics, and social sciences.(5) Maths supports students to “understand why patterns hold, why strategies work, how data tells a story, and … reason whether statements are true.”(6)
Good maths understandings have wider societal impacts, too, with positive links to “economic success and civic participation.”(7) At the other end, poor mathematics results in schools have been shown to have a significant negative impact on national economies. (8) Maths matters, well beyond the classroom context.
The early years of school are an important time for maths learning “"Early achievement in mathematics is a strong predictor – even more so than reading skills – of later academic achievement, mobility, economic success, and civic participation”" – Royal Society Expert Advisory Panel, 2021(9)
Years 1-3 of primary school are critical for maths learning. Understandings that are developed during these years set students up for success – or struggle – for the rest of their maths journey throughout schooling and into adulthood. Primary school maths builds on the foundations of early learning and provides the mathematical understanding that is needed for more complex learning in the senior school and beyond.
Students will have already built some basic maths skills through play-based early childhood education experiences.(10) For example, most students will have started learning to identify, understand, count, and compare numbers. Maths learning becomes more formalised once students enter primary school.
Years 1-3 is the time that students develop:
- their foundational understanding of number concepts and skills, measurement, algebra, spatial reasoning, geometry, and statistics
- positive or negative attitudes towards maths,(11) and the self-belief in their ability to do maths.(12)
The quality of maths teaching during Years 1-3 has long-lasting impacts for students.(13) Studies have shown that maths achievement in the primary years is connected to later success across a range of life outcomes, like higher education achievement, better jobs, better income, and social mobility.(14)
Students’ experiences of maths during this time also influence their attitudes towards the subject, and their own view of themselves as capable, confident maths students – which also impacts their motivation and learning success.
However, national and international studies show that teachers and students aren’t as confident in maths as they could be. Concerning maths results from late primary school and beyond have their roots in the preparation that students receive – or don’t – in their early years at school. Building a strong foundation of early maths skills, concepts, and understandings is crucial to later success.
Building maths understandings is the key to success
The early years of primary school are when vital maths understandings are taught. Building these core understandings matter much more than the ability to always get an answer 'correct'. In fact, an 'incorrect' answer is a valuable opportunity to explore concepts more deeply and address any misconceptions.
Teaching students shortcuts may help them get correct answers in Years 1-3, but won't provide the solid grounding of understanding that is needed for the next parts of their maths journey. Without other quality teaching practices, students may form misunderstandings which lead to difficulties in later learning.
What we did
This study looked at good practice in the teaching of maths in early primary (Years 1-3). ERO explored:
- What is good practice in improving maths in early primary school?
- What does the evidence say about improving maths in the early primary years?
- What does this look like in our real-life practice in the Aotearoa New Zealand context, across a range of schools?
- What insights, strategies, and examples can we gather that could be useful for teachers?
There is a companion guide to this report. There is a companion guide to this report. From part 3 of this report provides practical information on teaching maths in Years 1-3. This information is also available in a shorter guide for teachers available on ERO’s evidence website.
How we looked at good practice
To understand what good maths teaching looks like in the early years of school, we carried out an in-depth review of research from Aotearoa New Zealand and overseas. Using the evidence base, we developed a set of nine ‘practice areas’ that illustrate key aspects of good practice in teaching maths in Years 1 to 3. (These are the areas of practice that are detailed in Part 3 of this report.)
ERO then visited a selection of primary schools to find out how they make these good maths practices happen in real life. The schools we visited represented a range of settings, communities, deciles, roll size, ethnic diversity, and urban and rural locations across the country. As part of our visits to 12 schools, we observed maths in 24 classes and spoke to:
- 24 teachers
- 20 school leaders, including principals, deputy principals, and maths curriculum leaders. Some of these leaders also had teaching roles
- students from Years 1-3 in each class we visited.
We also looked at samples of assessment, planning documents, and professional development resources.
This research is focused on good practice in Years 1-3 maths, in state and state-integrated English-medium schools.
Report structure
This report is divided into 3 main parts, along with introductory and concluding sections.
About this report provides a rationale for undertaking this work, outlining what ERO did and showing why maths teaching is so important.
Part 1 provides an overview of maths learning and teaching in Aotearoa New Zealand.
Part 2 outlines the foundations that enable good teaching practices: teachers having good knowledge themselves, and working within a supportive, maths-focused school culture and curriculum.
Part 3 describes and illustrates the nine key areas of practice that national and international research highlight as particularly effective in teaching maths to Years 1-3.
Conclusion summarises what we found out, and what this means for teachers moving forward.
Useful resources provides some practical maths-related resources for teachers and leaders.
This report is for teachers of Years 1 to 3. It draws on research and real-life stories and strategies to shine a light on the key ways that teachers can most effectively teach maths to students in the first years of primary school.
Why we did this research
Maths is important – and not just in the classroom. It helps us understand our world. Mathematical knowledge is a building block of important life skills like problem solving, communication, and creative thinking. However, student and teacher confidence in maths is often lower than in other subjects.(1) It is common to hear both adults and children say they are ‘bad at maths’, or that maths is ‘only for some people’.(2)
It doesn’t have to be like this. Confidence and capabilIty in maths can be developed. The early years of primary school are when students develop their key maths skills and understandings. The experiences, attitudes, and expectations formed at this time greatly influence future success in maths.
The quality of maths teaching makes a big difference for students’ confidence and capability, particularly in the early years of primary school. In Years 1-3, students are forming understandings of crucial maths concepts that will set them up for future learning and educational success. This research and report share practical strategies for quality maths teaching in the early primary years, and shines a light on good practice. It is the aim of this research to lift teachers’ confidence and capability in this pivotal area of their practice. With improvements to maths teaching, all students can be supported to enjoy, find success, and benefit from maths.
“While most New Zealanders likely consider maths knowledge and skills important for our economy and valuable in broader society, many kaiako, teachers and students have encountered views like ‘I was never any good at maths’, or ‘I always hated maths’, or ‘What’s the point of maths?’. These societal perceptions can have a profound impact on maths learning.” – Ministry of Education, 2023. (3)
Maths knowledge has real-life impacts
We use maths every day, all our lives. It’s through maths that we pay for groceries, cook and bake, build houses, read a map, fly planes, split a dinner bill, knit a jumper, convert money when we’re overseas, create special effects for movies, make important life decisions, and save up for our first car. It is also an important part of understanding and interpreting what is happening in our world.
Students develop valuable skills like creative problem solving and logical reasoning through using mathematical processes, ideas, and concepts.(4) Maths learning helps people to view information critically, and drives learning success in areas like science, technology, economics, and social sciences.(5) Maths supports students to “understand why patterns hold, why strategies work, how data tells a story, and … reason whether statements are true.”(6)
Good maths understandings have wider societal impacts, too, with positive links to “economic success and civic participation.”(7) At the other end, poor mathematics results in schools have been shown to have a significant negative impact on national economies. (8) Maths matters, well beyond the classroom context.
The early years of school are an important time for maths learning “"Early achievement in mathematics is a strong predictor – even more so than reading skills – of later academic achievement, mobility, economic success, and civic participation”" – Royal Society Expert Advisory Panel, 2021(9)
Years 1-3 of primary school are critical for maths learning. Understandings that are developed during these years set students up for success – or struggle – for the rest of their maths journey throughout schooling and into adulthood. Primary school maths builds on the foundations of early learning and provides the mathematical understanding that is needed for more complex learning in the senior school and beyond.
Students will have already built some basic maths skills through play-based early childhood education experiences.(10) For example, most students will have started learning to identify, understand, count, and compare numbers. Maths learning becomes more formalised once students enter primary school.
Years 1-3 is the time that students develop:
- their foundational understanding of number concepts and skills, measurement, algebra, spatial reasoning, geometry, and statistics
- positive or negative attitudes towards maths,(11) and the self-belief in their ability to do maths.(12)
The quality of maths teaching during Years 1-3 has long-lasting impacts for students.(13) Studies have shown that maths achievement in the primary years is connected to later success across a range of life outcomes, like higher education achievement, better jobs, better income, and social mobility.(14)
Students’ experiences of maths during this time also influence their attitudes towards the subject, and their own view of themselves as capable, confident maths students – which also impacts their motivation and learning success.
However, national and international studies show that teachers and students aren’t as confident in maths as they could be. Concerning maths results from late primary school and beyond have their roots in the preparation that students receive – or don’t – in their early years at school. Building a strong foundation of early maths skills, concepts, and understandings is crucial to later success.
Building maths understandings is the key to success
The early years of primary school are when vital maths understandings are taught. Building these core understandings matter much more than the ability to always get an answer 'correct'. In fact, an 'incorrect' answer is a valuable opportunity to explore concepts more deeply and address any misconceptions.
Teaching students shortcuts may help them get correct answers in Years 1-3, but won't provide the solid grounding of understanding that is needed for the next parts of their maths journey. Without other quality teaching practices, students may form misunderstandings which lead to difficulties in later learning.
What we did
This study looked at good practice in the teaching of maths in early primary (Years 1-3). ERO explored:
- What is good practice in improving maths in early primary school?
- What does the evidence say about improving maths in the early primary years?
- What does this look like in our real-life practice in the Aotearoa New Zealand context, across a range of schools?
- What insights, strategies, and examples can we gather that could be useful for teachers?
There is a companion guide to this report. There is a companion guide to this report. From part 3 of this report provides practical information on teaching maths in Years 1-3. This information is also available in a shorter guide for teachers available on ERO’s evidence website.
How we looked at good practice
To understand what good maths teaching looks like in the early years of school, we carried out an in-depth review of research from Aotearoa New Zealand and overseas. Using the evidence base, we developed a set of nine ‘practice areas’ that illustrate key aspects of good practice in teaching maths in Years 1 to 3. (These are the areas of practice that are detailed in Part 3 of this report.)
ERO then visited a selection of primary schools to find out how they make these good maths practices happen in real life. The schools we visited represented a range of settings, communities, deciles, roll size, ethnic diversity, and urban and rural locations across the country. As part of our visits to 12 schools, we observed maths in 24 classes and spoke to:
- 24 teachers
- 20 school leaders, including principals, deputy principals, and maths curriculum leaders. Some of these leaders also had teaching roles
- students from Years 1-3 in each class we visited.
We also looked at samples of assessment, planning documents, and professional development resources.
This research is focused on good practice in Years 1-3 maths, in state and state-integrated English-medium schools.
Report structure
This report is divided into 3 main parts, along with introductory and concluding sections.
About this report provides a rationale for undertaking this work, outlining what ERO did and showing why maths teaching is so important.
Part 1 provides an overview of maths learning and teaching in Aotearoa New Zealand.
Part 2 outlines the foundations that enable good teaching practices: teachers having good knowledge themselves, and working within a supportive, maths-focused school culture and curriculum.
Part 3 describes and illustrates the nine key areas of practice that national and international research highlight as particularly effective in teaching maths to Years 1-3.
Conclusion summarises what we found out, and what this means for teachers moving forward.
Useful resources provides some practical maths-related resources for teachers and leaders.
Part 1: Maths in Aotearoa New Zealand
Aotearoa New Zealand’s maths achievement has declined in recent years, and not all teachers are confident about teaching maths. It’s important that improvements are made to maths teaching and learning.
What does maths look like in our schools?
Maths learning content is set by the national curriculum, but the detail of how maths is taught is not currently mandated.(16) Most teachers use learning progressions or frameworks to help understand students’ knowledge and skills as they progress through the curriculum.
How well are our students doing in maths?
ERO has been reporting for some time that our national maths achievement picture is concerning. In 2013 ERO looked at maths in Years 4 to 8, noting that the education system continued to under-perform for some students and that we had a wider spread of achievement compared to other high performing countries. In 2016 we released a guide for supporting learning in the early years. Our 2018 report focused on effective teaching strategies in mathematics, noting trends that show that Year 8 students are less confident in maths than Year 4 students.
While national and international assessment studies are undertaken after the Year 1-3 period of schooling, it’s useful to remember that results from later primary school and beyond have their roots in the preparation that students receive – or don’t – in earlier years.
At ages 9-10 we are not doing as well in maths compared to other countries
The Trends in International Mathematics and Science Study (TIMSS) is an educational research study on global student achievement in mathematics and science of students aged nine to 10 and 13-14 (Year 5 and Year 10) in over 60 countries. The 2018/19 TIMSS study showed that Year 5 students in Aotearoa New Zealand underperformed in three key topic areas.(17) (See Figure 2.)
Figure 2: Percentage of Year 5 students who scored lower than the international average in three key mathematical topics [2018/19]
![Figure 2: Percentage of Year 5 students who scored lower than the international average in three key mathematical topics [2018/19]](/media/mejd2wpm/report-figure-2.png?rmode=max&width=500)
The maths skills and knowledge of our 15-year-olds is declining. Results from the 2022 Programme for International Student Assessment (PISA) study, which assesses the knowledge and skills of half a million 15-year-old students in mathematics in 81 countries , shows our results have seen a significant decline over the last 20 years. (See Figure 3.)(19) In 2022, Aotearoa New Zealand’s average mathematics score was above the OECD average, but lower than 2003-2018.
Figure 3: Aotearoa New Zealand and OECD mean mathematics scores, 2003-2022
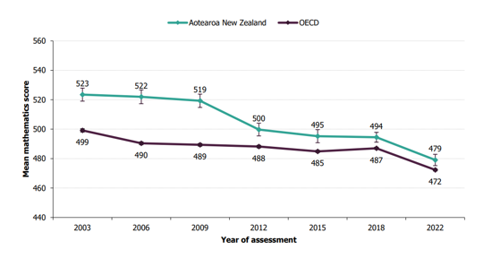
Notes: Error bars on the graph provide a 95% confidence interval for the estimate of the average. The OECD mean shown is based on as many of the 38 countries that have data available. These estimates differ slightly from the OECD reports as they include more countries. Luxembourg did not participate in 2022.
Source: OECD, 2023(20)
PISA’s 2022 results also show that, while Aotearoa New Zealand’s average mathematics score was above the OECD average, our maths achievement picture has a range of worrying features:
- the difference between our highest- and lowest- performers has widened and shifted down, and is among the widest in the OECD
- the proportion of “low” performers has increased since 2018 and almost doubled since 2003 (29 percent compared to 15 percent)
- the proportion of “high” performers (those who score Level 5 or above) has halved since 2003
- there is a higher difference between the scores of the lowest and highest advantaged students in New Zealand than the OECD average
- boys score higher than girls, on average, and a higher proportion of boys are high performers
- anxiety about maths has increased, and is higher than the OECD average, with girls reporting significantly higher anxiety than boys
- our students report a relatively negative maths learning environment compared to most other countries.
Students’ maths achievement declines as they go through school
Looking at domestic measures, students’ achievement declines from Year 4 as they move through primary school and onto secondary school.(21) The National Monitoring Study of Student Achievement (NMSSA) in 2022 shows that while most Year 4 students (82 percent) meet maths curriculum expectations, by Year 8, less than half (42 percent) meet expectations.(22) (See Figure 4.) This shows a concerning shift in students’ achievement between Year 4 and Year 8 – right when they are about to start secondary school.
Figure 4: Students meeting curriculum expectations in maths in 2022
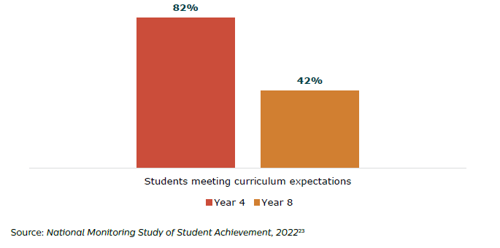
These achievement results indicate that young students are not being as well set up as they could be for their later, more complex maths learning. There is a cumulative effect on students’ ability to engage successfully and achieve in maths as they progress through school, so the foundational learning that happens in Years 1-3 is an important part of this picture.
National maths data is gathered from Year 4:
National maths achievement information is gathered through a sample of students in Year 4, just past the early years of primary school that we focus on in this report. However, it is useful to look at the Year 4 achievement picture, as well as achievement in later years, as a way of seeing the result of the learning that happens in Years 1-3.
Our students are experiencing maths anxiety
The 2022 PISA study shows that, compared to the OECD average, a larger proportion of our students are anxious about failing maths and worry maths class will be difficult for them.(24)
- Two-thirds (67 percent) of students worry about getting poor marks/grades in maths.
- Over half (62 percent) are anxious about failing maths.
- Students who are anxious about maths score 15 to 50 points lower (on average) than their non-anxious peers.
- Our girls report more anxiety about maths than boys.
Not all teachers are confident about teaching maths
ERO surveyed new primary teachers in 2023, finding that nearly a quarter (24 percent) felt ‘unprepared’ in their maths content knowledge when they first started.(25) A recent New Zealand Council of Education Research study also found that while most teachers enjoy teaching maths and agree it is important, teachers in junior primary school are less confident teaching all aspects of maths than their senior peers (comparing Year 4 and Year 8 teachers).(26)
This is concerning, as it has been established that effective teachers of maths require maths knowledge that is ‘well beyond the student level’.(27) Primary school teachers are generalists and very few have specialised in mathematics or mathematics teaching, meaning that there is limited expertise in the sector. We talk more about the importance of foundational teacher knowledge in Part 2 of this report.
The limited confidence of teachers in maths, combined with poor student achievement, indicates that teachers are not as well set up as they could be. Studies have shown that when teachers aren’t confident about the best way to teach, they often revert to how they were taught – and this won’t always be effective.(28)
Conclusion
Our national achievement picture is concerning, and not all teachers feel prepared to engage students in this crucial area of their schooling. We know that maths is the pathway to success in many other learning areas as well as having longer-term benefits, which means early maths has big impacts for learning and life outcomes.
Improvement is possible. In the early years of primary school, teachers have the opportunity to set the scene for their young maths students. Through skilful maths teaching in the early years of primary school, students can be supported to form foundational understandings of maths concepts, and of their own capability as maths students. Now is the time to support Year 1-3 teachers with clear, up-to-date messages about what practices really make the difference.
Aotearoa New Zealand’s maths achievement has declined in recent years, and not all teachers are confident about teaching maths. It’s important that improvements are made to maths teaching and learning.
What does maths look like in our schools?
Maths learning content is set by the national curriculum, but the detail of how maths is taught is not currently mandated.(16) Most teachers use learning progressions or frameworks to help understand students’ knowledge and skills as they progress through the curriculum.
How well are our students doing in maths?
ERO has been reporting for some time that our national maths achievement picture is concerning. In 2013 ERO looked at maths in Years 4 to 8, noting that the education system continued to under-perform for some students and that we had a wider spread of achievement compared to other high performing countries. In 2016 we released a guide for supporting learning in the early years. Our 2018 report focused on effective teaching strategies in mathematics, noting trends that show that Year 8 students are less confident in maths than Year 4 students.
While national and international assessment studies are undertaken after the Year 1-3 period of schooling, it’s useful to remember that results from later primary school and beyond have their roots in the preparation that students receive – or don’t – in earlier years.
At ages 9-10 we are not doing as well in maths compared to other countries
The Trends in International Mathematics and Science Study (TIMSS) is an educational research study on global student achievement in mathematics and science of students aged nine to 10 and 13-14 (Year 5 and Year 10) in over 60 countries. The 2018/19 TIMSS study showed that Year 5 students in Aotearoa New Zealand underperformed in three key topic areas.(17) (See Figure 2.)
Figure 2: Percentage of Year 5 students who scored lower than the international average in three key mathematical topics [2018/19]
![Figure 2: Percentage of Year 5 students who scored lower than the international average in three key mathematical topics [2018/19]](/media/mejd2wpm/report-figure-2.png?rmode=max&width=500)
The maths skills and knowledge of our 15-year-olds is declining. Results from the 2022 Programme for International Student Assessment (PISA) study, which assesses the knowledge and skills of half a million 15-year-old students in mathematics in 81 countries , shows our results have seen a significant decline over the last 20 years. (See Figure 3.)(19) In 2022, Aotearoa New Zealand’s average mathematics score was above the OECD average, but lower than 2003-2018.
Figure 3: Aotearoa New Zealand and OECD mean mathematics scores, 2003-2022

Notes: Error bars on the graph provide a 95% confidence interval for the estimate of the average. The OECD mean shown is based on as many of the 38 countries that have data available. These estimates differ slightly from the OECD reports as they include more countries. Luxembourg did not participate in 2022.
Source: OECD, 2023(20)
PISA’s 2022 results also show that, while Aotearoa New Zealand’s average mathematics score was above the OECD average, our maths achievement picture has a range of worrying features:
- the difference between our highest- and lowest- performers has widened and shifted down, and is among the widest in the OECD
- the proportion of “low” performers has increased since 2018 and almost doubled since 2003 (29 percent compared to 15 percent)
- the proportion of “high” performers (those who score Level 5 or above) has halved since 2003
- there is a higher difference between the scores of the lowest and highest advantaged students in New Zealand than the OECD average
- boys score higher than girls, on average, and a higher proportion of boys are high performers
- anxiety about maths has increased, and is higher than the OECD average, with girls reporting significantly higher anxiety than boys
- our students report a relatively negative maths learning environment compared to most other countries.
Students’ maths achievement declines as they go through school
Looking at domestic measures, students’ achievement declines from Year 4 as they move through primary school and onto secondary school.(21) The National Monitoring Study of Student Achievement (NMSSA) in 2022 shows that while most Year 4 students (82 percent) meet maths curriculum expectations, by Year 8, less than half (42 percent) meet expectations.(22) (See Figure 4.) This shows a concerning shift in students’ achievement between Year 4 and Year 8 – right when they are about to start secondary school.
Figure 4: Students meeting curriculum expectations in maths in 2022

These achievement results indicate that young students are not being as well set up as they could be for their later, more complex maths learning. There is a cumulative effect on students’ ability to engage successfully and achieve in maths as they progress through school, so the foundational learning that happens in Years 1-3 is an important part of this picture.
National maths data is gathered from Year 4:
National maths achievement information is gathered through a sample of students in Year 4, just past the early years of primary school that we focus on in this report. However, it is useful to look at the Year 4 achievement picture, as well as achievement in later years, as a way of seeing the result of the learning that happens in Years 1-3.
Our students are experiencing maths anxiety
The 2022 PISA study shows that, compared to the OECD average, a larger proportion of our students are anxious about failing maths and worry maths class will be difficult for them.(24)
- Two-thirds (67 percent) of students worry about getting poor marks/grades in maths.
- Over half (62 percent) are anxious about failing maths.
- Students who are anxious about maths score 15 to 50 points lower (on average) than their non-anxious peers.
- Our girls report more anxiety about maths than boys.
Not all teachers are confident about teaching maths
ERO surveyed new primary teachers in 2023, finding that nearly a quarter (24 percent) felt ‘unprepared’ in their maths content knowledge when they first started.(25) A recent New Zealand Council of Education Research study also found that while most teachers enjoy teaching maths and agree it is important, teachers in junior primary school are less confident teaching all aspects of maths than their senior peers (comparing Year 4 and Year 8 teachers).(26)
This is concerning, as it has been established that effective teachers of maths require maths knowledge that is ‘well beyond the student level’.(27) Primary school teachers are generalists and very few have specialised in mathematics or mathematics teaching, meaning that there is limited expertise in the sector. We talk more about the importance of foundational teacher knowledge in Part 2 of this report.
The limited confidence of teachers in maths, combined with poor student achievement, indicates that teachers are not as well set up as they could be. Studies have shown that when teachers aren’t confident about the best way to teach, they often revert to how they were taught – and this won’t always be effective.(28)
Conclusion
Our national achievement picture is concerning, and not all teachers feel prepared to engage students in this crucial area of their schooling. We know that maths is the pathway to success in many other learning areas as well as having longer-term benefits, which means early maths has big impacts for learning and life outcomes.
Improvement is possible. In the early years of primary school, teachers have the opportunity to set the scene for their young maths students. Through skilful maths teaching in the early years of primary school, students can be supported to form foundational understandings of maths concepts, and of their own capability as maths students. Now is the time to support Year 1-3 teachers with clear, up-to-date messages about what practices really make the difference.
Part 2: Enablers for good teaching
This report is mostly focused on how teachers can teach maths in their classrooms. There are also foundations that need to be in place before teachers can do their best maths teaching.
To be well set up, teachers need a strong understanding of maths themselves, and a supportive school culture and curriculum.
Overview of this section
This part of the report sets out the foundations that are needed for good maths teaching. It includes:
- what is important for teachers to know about maths
- how school culture and curriculum can support effective maths practice.
1) What is important for teachers to know about maths?
Teachers get their knowledge about teaching maths through their own schooling experiences, their Initial teacher education, and through their ongoing learning once in the role. Their maths teaching practices and expectations of students are informed by their own maths-related learning, along with their personal beliefs and experiences.(29)
Teachers need good maths content knowledge
Teaching maths requires an understanding of the maths content that is beyond (rather than at or below) the level of the content being taught.(30) This might be a challenge for those teachers who consider themselves ‘not really maths people’. To support students to build their understanding, teachers themselves need to properly understand the concepts and ideas that sit behind Year 1-3 maths content, as well as the content that will be covered in the senior levels of primary school.
“Unless teachers make good sense of the mathematical ideas, they will not have the confidence to press for student understanding… [or] the flexibility they need for spotting the entry points that will move students towards more sophisticated and mathematically grounded understandings.”
– Anthony & Walshaw, 2007(31)
Teachers need good knowledge of how maths is learnt
Teachers are well set up to teach maths when they are clear and up-to-date about how maths learning works. This means knowing about how children learn maths, how to structure and sequence ideas to build understandings, what practices work best for teaching specific aspects of maths for this age group, and how to recognise what progress looks like.(32) Without this current knowledge, it can be tempting for teachers to return to familiar practices from their own schooling, which may no longer be useful. The risk of using dated or under-informed practices is that they can result in students misunderstanding basic maths ideas (having misconceptions or ‘alternative conceptions’). (33)
What do we know about how children learn maths at this age?
The evidence shows that the development of children’s maths understandings involves:
- growing skills, factual knowledge, and conceptual understandings across a range of topic areas, including quantity and number, operations, shape, and space
- forming connections between concepts – such as understanding that addition is the inverse of subtraction
- building reasoning skills – such as logical thinking and the ability to justify and explain ideas.(34)
Teachers need to know what progress looks like
Teachers need a solid understanding of the sequenced learning that sits behind core maths concepts, how they connect each other, and the best ways to support children to learn about them.(35) Understanding typical maths progress equips teachers to confidently recognise learning and make good decisions about what should be taught next.
In practice, this looks like teachers:
- building on understandings from their own experience and Initial Teacher Education
- accessing new evidence about maths learning and teaching
- having maths-focused discussions and knowledge-building with colleagues and experts
- having clear understandings of the maths level of the tasks they set for their students
- extending the most capable students and accelerating those who are struggling
- knowing when to ask for help from more knowledgeable peers and experts
- reflecting on the effectiveness of their teaching in relation to what they know about maths progression steps and how they should be developed.
“Effective mathematics teaching requires knowledge of mathematics pedagogy and learning as well as of mathematics itself. This includes knowledge of how children learn mathematical concepts, connections between mathematical concepts, likely difficulties children may have, and different approaches to solving problems or tasks.”
- Clark, Henderson, and Gifford, 2020(36)
2) How school culture and a whole school curriculum can support effective maths practice
The whole school curriculum can provide a clear, structured framework for maths teaching
Teachers who are confident and familiar with what progress and progression steps look like, including at lower and higher levels than are typical for their class, are better equipped to teach responsively. This is easiest when schools take a proactive approach to ensuring that all teachers have regular opportunities to learn and revisit expectations for the maths teaching and learning, and develop shared understandings of maths progression steps. A school-wide approach helps teachers to see the broader picture – where the learning that happens in this class fits in to the maths learning trajectory across the whole school. Consistency of understanding across teaching teams also helps make sure that information-sharing is as useful and relevant as possible when students move classes.
Effective school settings outline their expectations for teaching and learning through their localised curriculum.(37) A localised curriculum clarifies how the national curriculum is taught and monitored at an individual school. Among other things, it should include statements about what good maths learning looks like, clear expectations for teachers’ practice, and planning for how maths knowledge and competency is built over years at the school. It will include coverage of key concepts (or ‘big ideas’) that students need to build knowledge of in Years 1-3. Key concepts include number and operations, algebra and patterning, measurement, space and shape, and statistics and probability. The curriculum should also set out clear progress markers and explicit assessment criteria.
Shared understandings of their local maths curriculum can be supported through schools:
- having clear documentation, templates and guidance
- facilitating teacher discussion at planning and professional learning meetings about:
- maths concepts
- teaching practices
- how students are progressing
- providing modelling and observation opportunities in maths classrooms
- partnering with parents/whānau and supporting their community to understand the maths teaching and learning that happens at this school.
What are learning progressions?
The evidence shows that a structured and sequenced approach to maths learning works best, to help young students make essential links and connections.
There are typical paths of sequenced learning and skill development that go into successfully understanding different maths ideas.(38) These typical paths can be described as developmental or learning progressions, or progression markers or steps.
Often, learning progressions are represented as a spiral pattern, to show that maths learning is not a linear process and some steps may need to be revisited. Two examples of progression step diagrams are shown below.(39)
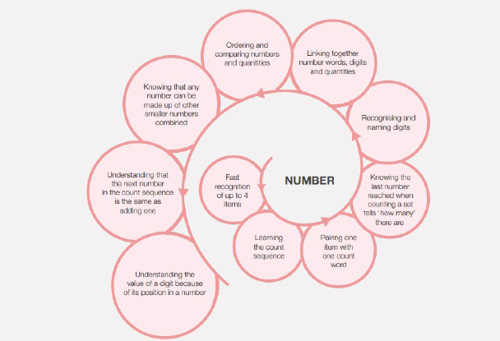
In Aotearoa New Zealand schools define their expectations for how maths progress is measured as part of their localisation of the national curriculum expectations. This means that each school’s curriculum documents should provide teachers with clear, shared expectations of what sequenced maths progress looks like at their school.
The teaching and learning of maths should be prioritised and valued at the school
Teachers are well set up when they work in schools that prioritise and actively support evidence-based maths teaching. It helps when school leaders take action to lift the profile of maths at their school, clearly communicating to teachers that maths is a top priority in the teaching and learning that happens at this school. We know that maths is an area of teaching where teachers are not always confident, and maths anxiety is common in adults, so it is an area that is more likely than others to be undervalued or avoided. Effective school settings make deliberate moves to promote awareness of maths, demystify maths teaching, and show that maths is important. This might include schools:
- carefully timetabling to maximise opportunities to learn
- arranging regular collaborative planning sessions
- providing professional learning and support opportunities
- highlighting and celebrating maths achievements
- allocating resources to maths teaching and learning.
It is useful to have a culture of being open to learning, sharing, and improving
Effective school settings have strong leadership practices which promote a culture of being open to learning and dedicated to constantly improving maths teaching.(40) Leaders can also help teachers through clear messages about “collective teacher efficacy” - how the team can positively shift their students’ achievement outcomes and use evidence to understand how they do make a difference.(41)
Good school systems for monitoring and analysing student progress are important in understanding which aspects of their maths teaching are going well, and where teachers and leaders can target their efforts for improvement. Teachers require regular opportunities to learn about effective maths strategies and to reflect on which practices work best for their students. Leaders can support this by providing opportunities for teachers to share their maths learning and ideas with other teachers.
“[At this school] teachers are very willing to try new things. [They are an] experimental and open-minded group of teachers.” – School leader
Real-life example: effective school culture
One large urban school, with high numbers of Māori and Pacific students, demonstrates an effective school culture focused on maths teaching improvements.
Leaders and teachers had previously worked together to review their maths programme in relation to strategic planning documents Action Plan for Pacific Education and Ka Hikitia.[i] They share that leaders and teachers at the school purposefully maintain a sense of ‘growth mindset’: “We wanted to fix old habits by changing our thinking, which means we do things differently”.
Leaders and teachers begin the review process by looking at both national maths data and their own achievement data. This challenges them to look at their own practice – including video-recording their own maths teaching sessions and reflecting on them. Teachers use these to review what they are doing and look at how students react to learning activities. Reflective discussions use phrases like: “I notice this..” and “I am responding by…” to help teachers reflect on the maths and share their learning with others.
The school forms a cluster group with neighbouring schools and works with an external professional learning provider to help them look at how to improve engagement through enriching their maths programmes, discuss challenges they are facing in maths, and how to get to grips with proposed curriculum changes.
“We didn’t want a PLD model that just knocks teachers over the head. It’s better to discuss, challenge, and plan in a safe space with peers.” - Principal
These cluster professional learning sessions occur twice a term and each school undertakes follow-up workshops at their schools. Teachers ‘take a student’s perspective’ in the workshops as they engage in maths activities, as well as discussing maths research literature. The sessions are characterised by excitement and enthusiasm as they come together and bring examples of practice, and discuss how they assess their students. Teachers share resources and ideas for maths teaching strategies. Leaders and teachers report that they continue to grow in confidence to bring along their challenges and successes to these collaborative sessions.
Conclusion
Great maths teaching won’t just happen by itself. It’s not possible to put good strategies in place when key knowledge, skills, or supports aren’t there yet. Foundations need to be in place to ensure there is a strong platform to build on.
Teachers need solid, basic knowledge about maths skills, knowledge, and concepts. On top of this, they require an up-to-date understanding of the structures and strategies that support young students to learn maths. This is particularly important in the early years, to avoid setting up misconceptions which impact on later learning.
School settings set the scene for good maths practice. A supportive and improvement-focused culture is essential, along with a clear localised curriculum which articulates what maths learning and progress looks like.
This report is mostly focused on how teachers can teach maths in their classrooms. There are also foundations that need to be in place before teachers can do their best maths teaching.
To be well set up, teachers need a strong understanding of maths themselves, and a supportive school culture and curriculum.
Overview of this section
This part of the report sets out the foundations that are needed for good maths teaching. It includes:
- what is important for teachers to know about maths
- how school culture and curriculum can support effective maths practice.
1) What is important for teachers to know about maths?
Teachers get their knowledge about teaching maths through their own schooling experiences, their Initial teacher education, and through their ongoing learning once in the role. Their maths teaching practices and expectations of students are informed by their own maths-related learning, along with their personal beliefs and experiences.(29)
Teachers need good maths content knowledge
Teaching maths requires an understanding of the maths content that is beyond (rather than at or below) the level of the content being taught.(30) This might be a challenge for those teachers who consider themselves ‘not really maths people’. To support students to build their understanding, teachers themselves need to properly understand the concepts and ideas that sit behind Year 1-3 maths content, as well as the content that will be covered in the senior levels of primary school.
“Unless teachers make good sense of the mathematical ideas, they will not have the confidence to press for student understanding… [or] the flexibility they need for spotting the entry points that will move students towards more sophisticated and mathematically grounded understandings.”
– Anthony & Walshaw, 2007(31)
Teachers need good knowledge of how maths is learnt
Teachers are well set up to teach maths when they are clear and up-to-date about how maths learning works. This means knowing about how children learn maths, how to structure and sequence ideas to build understandings, what practices work best for teaching specific aspects of maths for this age group, and how to recognise what progress looks like.(32) Without this current knowledge, it can be tempting for teachers to return to familiar practices from their own schooling, which may no longer be useful. The risk of using dated or under-informed practices is that they can result in students misunderstanding basic maths ideas (having misconceptions or ‘alternative conceptions’). (33)
What do we know about how children learn maths at this age?
The evidence shows that the development of children’s maths understandings involves:
- growing skills, factual knowledge, and conceptual understandings across a range of topic areas, including quantity and number, operations, shape, and space
- forming connections between concepts – such as understanding that addition is the inverse of subtraction
- building reasoning skills – such as logical thinking and the ability to justify and explain ideas.(34)
Teachers need to know what progress looks like
Teachers need a solid understanding of the sequenced learning that sits behind core maths concepts, how they connect each other, and the best ways to support children to learn about them.(35) Understanding typical maths progress equips teachers to confidently recognise learning and make good decisions about what should be taught next.
In practice, this looks like teachers:
- building on understandings from their own experience and Initial Teacher Education
- accessing new evidence about maths learning and teaching
- having maths-focused discussions and knowledge-building with colleagues and experts
- having clear understandings of the maths level of the tasks they set for their students
- extending the most capable students and accelerating those who are struggling
- knowing when to ask for help from more knowledgeable peers and experts
- reflecting on the effectiveness of their teaching in relation to what they know about maths progression steps and how they should be developed.
“Effective mathematics teaching requires knowledge of mathematics pedagogy and learning as well as of mathematics itself. This includes knowledge of how children learn mathematical concepts, connections between mathematical concepts, likely difficulties children may have, and different approaches to solving problems or tasks.”
- Clark, Henderson, and Gifford, 2020(36)
2) How school culture and a whole school curriculum can support effective maths practice
The whole school curriculum can provide a clear, structured framework for maths teaching
Teachers who are confident and familiar with what progress and progression steps look like, including at lower and higher levels than are typical for their class, are better equipped to teach responsively. This is easiest when schools take a proactive approach to ensuring that all teachers have regular opportunities to learn and revisit expectations for the maths teaching and learning, and develop shared understandings of maths progression steps. A school-wide approach helps teachers to see the broader picture – where the learning that happens in this class fits in to the maths learning trajectory across the whole school. Consistency of understanding across teaching teams also helps make sure that information-sharing is as useful and relevant as possible when students move classes.
Effective school settings outline their expectations for teaching and learning through their localised curriculum.(37) A localised curriculum clarifies how the national curriculum is taught and monitored at an individual school. Among other things, it should include statements about what good maths learning looks like, clear expectations for teachers’ practice, and planning for how maths knowledge and competency is built over years at the school. It will include coverage of key concepts (or ‘big ideas’) that students need to build knowledge of in Years 1-3. Key concepts include number and operations, algebra and patterning, measurement, space and shape, and statistics and probability. The curriculum should also set out clear progress markers and explicit assessment criteria.
Shared understandings of their local maths curriculum can be supported through schools:
- having clear documentation, templates and guidance
- facilitating teacher discussion at planning and professional learning meetings about:
- maths concepts
- teaching practices
- how students are progressing
- providing modelling and observation opportunities in maths classrooms
- partnering with parents/whānau and supporting their community to understand the maths teaching and learning that happens at this school.
What are learning progressions?
The evidence shows that a structured and sequenced approach to maths learning works best, to help young students make essential links and connections.
There are typical paths of sequenced learning and skill development that go into successfully understanding different maths ideas.(38) These typical paths can be described as developmental or learning progressions, or progression markers or steps.
Often, learning progressions are represented as a spiral pattern, to show that maths learning is not a linear process and some steps may need to be revisited. Two examples of progression step diagrams are shown below.(39)


In Aotearoa New Zealand schools define their expectations for how maths progress is measured as part of their localisation of the national curriculum expectations. This means that each school’s curriculum documents should provide teachers with clear, shared expectations of what sequenced maths progress looks like at their school.
The teaching and learning of maths should be prioritised and valued at the school
Teachers are well set up when they work in schools that prioritise and actively support evidence-based maths teaching. It helps when school leaders take action to lift the profile of maths at their school, clearly communicating to teachers that maths is a top priority in the teaching and learning that happens at this school. We know that maths is an area of teaching where teachers are not always confident, and maths anxiety is common in adults, so it is an area that is more likely than others to be undervalued or avoided. Effective school settings make deliberate moves to promote awareness of maths, demystify maths teaching, and show that maths is important. This might include schools:
- carefully timetabling to maximise opportunities to learn
- arranging regular collaborative planning sessions
- providing professional learning and support opportunities
- highlighting and celebrating maths achievements
- allocating resources to maths teaching and learning.
It is useful to have a culture of being open to learning, sharing, and improving
Effective school settings have strong leadership practices which promote a culture of being open to learning and dedicated to constantly improving maths teaching.(40) Leaders can also help teachers through clear messages about “collective teacher efficacy” - how the team can positively shift their students’ achievement outcomes and use evidence to understand how they do make a difference.(41)
Good school systems for monitoring and analysing student progress are important in understanding which aspects of their maths teaching are going well, and where teachers and leaders can target their efforts for improvement. Teachers require regular opportunities to learn about effective maths strategies and to reflect on which practices work best for their students. Leaders can support this by providing opportunities for teachers to share their maths learning and ideas with other teachers.
“[At this school] teachers are very willing to try new things. [They are an] experimental and open-minded group of teachers.” – School leader
Real-life example: effective school culture
One large urban school, with high numbers of Māori and Pacific students, demonstrates an effective school culture focused on maths teaching improvements.
Leaders and teachers had previously worked together to review their maths programme in relation to strategic planning documents Action Plan for Pacific Education and Ka Hikitia.[i] They share that leaders and teachers at the school purposefully maintain a sense of ‘growth mindset’: “We wanted to fix old habits by changing our thinking, which means we do things differently”.
Leaders and teachers begin the review process by looking at both national maths data and their own achievement data. This challenges them to look at their own practice – including video-recording their own maths teaching sessions and reflecting on them. Teachers use these to review what they are doing and look at how students react to learning activities. Reflective discussions use phrases like: “I notice this..” and “I am responding by…” to help teachers reflect on the maths and share their learning with others.
The school forms a cluster group with neighbouring schools and works with an external professional learning provider to help them look at how to improve engagement through enriching their maths programmes, discuss challenges they are facing in maths, and how to get to grips with proposed curriculum changes.
“We didn’t want a PLD model that just knocks teachers over the head. It’s better to discuss, challenge, and plan in a safe space with peers.” - Principal
These cluster professional learning sessions occur twice a term and each school undertakes follow-up workshops at their schools. Teachers ‘take a student’s perspective’ in the workshops as they engage in maths activities, as well as discussing maths research literature. The sessions are characterised by excitement and enthusiasm as they come together and bring examples of practice, and discuss how they assess their students. Teachers share resources and ideas for maths teaching strategies. Leaders and teachers report that they continue to grow in confidence to bring along their challenges and successes to these collaborative sessions.
Conclusion
Great maths teaching won’t just happen by itself. It’s not possible to put good strategies in place when key knowledge, skills, or supports aren’t there yet. Foundations need to be in place to ensure there is a strong platform to build on.
Teachers need solid, basic knowledge about maths skills, knowledge, and concepts. On top of this, they require an up-to-date understanding of the structures and strategies that support young students to learn maths. This is particularly important in the early years, to avoid setting up misconceptions which impact on later learning.
School settings set the scene for good maths practice. A supportive and improvement-focused culture is essential, along with a clear localised curriculum which articulates what maths learning and progress looks like.
Part 3: What is good practice for maths teaching in Years 1-3?
We reviewed international and local evidence to find the most powerful teaching practices for promoting positive maths outcomes. These have been organised into nine practice areas which focus on what teachers can do to help Year 1-3 students develop foundational maths knowledge, skills, and understandings. We then visited schools and gathered examples of how teachers action these specific practices in the classroom.
This part of the report provides practical support for teachers. Each practice area is unpacked into key teacher practices with real-life examples.
This part of the report offers practical guidance for Year 1-3 teachers. It is divided into nine practice areas. Each has its own brief summary of the practice area and explanation of why it is so important for early maths learning. The areas are broken down into a few key teacher practices that make the most difference. These are illustrated by real-life strategies, insights, and ideas from Aotearoa New Zealand classrooms.
The nine practice areas are:
Practice Area 1: Teachers use their understanding of assessment and how students learn maths to ensure they all progress |
Practice Area 2: Teachers use quality teaching practice in maths |
Practice Area 3: Teachers provide dedicated maths time every day so all students engage meaningfully in learning |
Practice Area 4: Teachers notice when students require extra support for learning and provide effective targeted teaching |
Practice Area 5: Teachers use tools and representations to express mathematical concepts |
Practice Area 6: The classroom learning environment encourages mathematical thinking, collaboration, and the enjoyment of maths |
Practice Area 7: Teachers make the most of moments throughout the day to highlight and use maths |
Practice Area 8: Maths classes reflect the cultures of their students and their families / whānau |
Practice Area 9: Teachers work in partnership with families / whānau to support maths learning |
We reviewed international and local evidence to find the most powerful teaching practices for promoting positive maths outcomes. These have been organised into nine practice areas which focus on what teachers can do to help Year 1-3 students develop foundational maths knowledge, skills, and understandings. We then visited schools and gathered examples of how teachers action these specific practices in the classroom.
This part of the report provides practical support for teachers. Each practice area is unpacked into key teacher practices with real-life examples.
This part of the report offers practical guidance for Year 1-3 teachers. It is divided into nine practice areas. Each has its own brief summary of the practice area and explanation of why it is so important for early maths learning. The areas are broken down into a few key teacher practices that make the most difference. These are illustrated by real-life strategies, insights, and ideas from Aotearoa New Zealand classrooms.
The nine practice areas are:
Practice Area 1: Teachers use their understanding of assessment and how students learn maths to ensure they all progress |
Practice Area 2: Teachers use quality teaching practice in maths |
Practice Area 3: Teachers provide dedicated maths time every day so all students engage meaningfully in learning |
Practice Area 4: Teachers notice when students require extra support for learning and provide effective targeted teaching |
Practice Area 5: Teachers use tools and representations to express mathematical concepts |
Practice Area 6: The classroom learning environment encourages mathematical thinking, collaboration, and the enjoyment of maths |
Practice Area 7: Teachers make the most of moments throughout the day to highlight and use maths |
Practice Area 8: Maths classes reflect the cultures of their students and their families / whānau |
Practice Area 9: Teachers work in partnership with families / whānau to support maths learning |
Practice area 1: Teachers use their understanding of assessment and how students learn maths to ensure they all progress
This practice area is about teachers purposefully building on their students’ experiences and knowledge to help them make progress in their maths learning. To do this, teachers draw on their maths content knowledge and understanding of maths learning progressions, to provide responsive teaching and assessment.
When this is going well, teachers understand what each student brings to their maths learning, what they already know, and what their next steps for learning are. They use this knowledge to inform their teaching and monitor progress.
In this section, we set out why teachers’ knowledge of students and their use of progressions and assessment information is so important for supporting students’ progress. We also offer practical guidance on how teachers can build this area of their own practice.
Overview of this section
This part of the report sets out useful information about how teachers can build and draw on their knowledge of maths progressions and assessments. It includes:
- What is this practice area?
- Why is this important?
- What does good practice look like in real life?
- Good practice example
- Reflective questions for teachers
1) What is this practice area?
This practice area is about teachers using their knowledge of students and about how maths concepts connect and build on each other, to line up learning experiences in a deliberate way. To do this, they purposefully find out what students know, and combine this with their knowledge about progressions. This information is used along with targeted assessment tasks and tools to identify what students know, how well they are progressing, and how teaching can best support their next learning steps. Teachers need to be explicit about what students should know and be able to do, so that they can develop specific goals with students.
The key teaching practices discussed in this section are:
- teachers determine what students bring to their learning, and build on what they already know
- teachers actively notice, recognise, and respond to students’ progress as they engage in maths
- teachers use assessment and progressions to plan for, document, and monitor students’ progress.
2) Why is this important?
When teachers are clear about what students know and bring to their maths learning, they can focus their teaching plans in response. Evidence shows that when teachers are confident about their role within their students’ maths learning journey, they raise their expectations for achievement and better target their teaching to promote progress.(43)
Teacher expectations make a difference
Teacher expectations impact significantly on students’ engagement and achievement.(44) This is an important consideration in the first few years of school when students are establishing views of themselves as students of maths and capable mathematicians.(45)
Teachers’ expectations are built on their understandings of how students current typically move along maths progression steps in relation to their cognitive development, and in relation to their school’s local maths curriculum. Getting really clear in these understandings helps teachers to hold useful expectations for learning and progress, and plan effective teaching in response.
It is important that teachers gain an in-depth awareness of their students’ understanding, so that they can respond in a timely and effective way to move them forward. In Years 1-3, students take time to develop maths knowledge through exposure to a variety of strategies and contexts,(46) so teachers need to constantly check on how these are developing. At a young age, assessment is best done in a natural setting, in the context of the everyday maths programme.(47) Deliberate selection of assessments and tasks can have a motivating effect, promoting positive student attitudes and a sense of accomplishment.
Good-quality assessment information provides a basis for planning next learning steps and adapting and targeting teaching – across the class and for individual students. Assessment helps teachers to set up expectations and goals for students, and plan purposeful learning steps which they can monitor to inform their decisions to move on. Assessing students’ understanding and knowledge also helps teachers adapt their practice and understand how effective it is in promoting the learning and progress of their students.
3) What does this area of practice look like in real life?
As part of this study, we talked to teachers and school leaders about the strategies that have worked well in their experience. We’ve collected their ideas and strategies here. It is important to reflect carefully about which of these will benefit each school’s unique community and context. No strategies are one-size-fits-all so all these strategies won’t be the right fit for everyone.
The key teacher practices that we focus on are:
- teachers determine what students bring to their learning, and build on what they already know
- teachers actively notice, recognise and respond to students’ progress as they engage in maths
- teachers use assessment and progressions to plan for, document, and monitor students’ progress.
a) Teachers determine what students bring to their learning, and build on what they already know
Teachers can assess what students already know through a variety of methods in a variety of contexts: from using formal assessment tools, to monitoring and observation during class. This will include providing a range of opportunities to learn about students’ prior experiences, attitudes, and strengths in maths. Assessment information should be used to inform next steps for teaching and what students should learn next.
Teaching that draws on the knowledge and skills students bring to school helps them see the relevance and practical uses of maths in their own lives. This includes building on students’ intuitive and existing understandings about maths.
Real-life strategies
|
We heard from teachers and school leaders that it works well to… |
|
Talk purposefully to students about their experiences, attitudes, and strengths in maths. Teachers find different opportunities throughout the day to hold informal conversations with their students that are focused on maths. This can occur as teachers set up for a maths session, as they interact during break times or in the playground, and as they engage in maths learning. Some opening questions to find out about their learning or experiences of maths include: Do you help with cooking at home? What games do you play together as a family? What is your favourite part of maths? What maths are you good at? What is the biggest/smallest number you know? |
|
Talk to colleagues about students’ prior experiences and progress in maths. Teachers talked to us about timely discussions held with teachers from previous classes to find out about their students’ previous experiences and successes in maths. They also learn from their colleagues in different year levels about what maths progress looks like for students in their classes. This helps them know where the students are coming from and heading towards in their maths journey. Schools involved in local clusters or Kāhui Ako use these networks to find out about what maths learning looks like, from early childhood education through to secondary school. |
|
Use diagnostic assessment to identify areas of strength and needs. This can be done through interviews with students, or setting an assessment task which focuses on familiarity a specific area of maths (e.g., a measurement task which can show student’s familiarity with measuring the weight or length of an object). Teachers use a range of assessments to gain insight into students’ knowledge, strategies, and understanding in a range of areas. |
|
Use an open task to assess student understanding. Teachers set an open task and observe how a student tackles the problem. This helps them to gauge the student’s level of competence in using expected knowledge, procedures, or skills. Selecting a task that can be approached in a range of different ways helps students to demonstrate their ability, and indicate what their next learning steps will be. Sometimes this is done through a summative assessment on a recent topic where students are given a problem that can be approached at any level of the curriculum. In one school, teachers come together as a team to link what students have done and pull out evidence from the national maths curriculum – and use this to identify what children have done or need to do to build on this. |
b) Teachers actively notice, recognise, and respond to students’ progress as they engage in maths
Targeted observation and effective questioning helps teachers understand what and how students are thinking and progressing. This equips them to provide purposeful instruction and feedback that builds on student knowledge and addresses any misunderstandings. When selecting a task, teachers should consider its level of challenge so that they can be ready to notice, recognise, and respond to what students demonstrate about their understanding and knowledge as they engage in that task.(48)
Effective questioning also helps teachers to learn about students’ prior experiences, attitudes, and strengths in maths. For example, a teacher can encourage students to explain how they solved a problem, and prompt the student to make connections with a ‘big idea’ that the class is currently focusing on.
Real-life strategies
|
We heard from teachers and school leaders that it works well to… |
|
Observe students’ engagement and be ready to respond. Teachers take note of the knowledge or processes a student relies on when they approach a task or respond to a question. Teachers note and respond to that student by: · adapting the task · adjusting the pace of the session · making a task simpler or more complex · demonstrating with or providing additional equipment · following up immediately with an individualised session · using this information in a subsequent group session. |
|
Check in with students through fast feedback techniques. Teachers we spoke with use a range of strategies to prompt students to assess their own levels of understanding or progress. This is done in formal and informal ways, for example: · students showing how well they understand a concept, how confident they feel, or how well they coped with a task by giving a thumbs up/down/hovering hand, or rating their understanding with one to five fingers · using emojis to show how they are feeling about their learning or understanding · encouraging students to talk with their peers about their learning. |
|
Participate in hands-on sessions with colleagues to uncover the underlying concepts in maths tasks and games. In one school, staff regularly work together to interact with equipment and collaborate on maths tasks. One school’s maths lead teacher reflected, “If you can’t solve it yourself, then you can’t expect the children to.” In these sessions, teachers discuss how their students might respond to the task, considering possible misconceptions and how they could pivot the lesson to address these. Teachers then work together to write these predictions up into a shared resource of ‘anticipations’ they can draw on. |
|
Listen to students to assess their understanding as they use equipment and talk to their peers. Several teachers talked about how they have learned to hold back from helping students when they are challenged to solve a maths task, in order to listen to their reasoning and watch them as they apply prior knowledge and manipulated materials. This helps teachers to identify current knowledge and any misconceptions or errors in their thinking, and to set new goals. |
c) Teachers use assessment and progressions to plan for, document, and monitor students’ progress
Effective teachers use systematic assessment and recording methods to monitor students’ progress and record their strategies and knowledge.
It’s important to keep in mind that assessment isn’t all about tests. In addition to normed or standardised assessments, early years maths can be assessed through purposeful task-setting, discussions with students, observations of group work, and more. (See the box below, for considerations when selecting assessment tools and tasks.) Teachers need a solid understanding of the range of formal and informal ways they can assess and monitor progress, to be able to make informed, timely teaching decisions.
Assessment decisions and records are most useful when teachers link them to their school’s curriculum and progression steps. In practice, this involves teachers using and recording assessment alongside the school’s expectations of progress. This helps teachers to monitor students’ progress, motivate students, and know about the effectiveness of their teaching.
Selecting assessment tools and tasks
The purpose of assessment is to provide clarity about what a student knows or has recently learnt, what they might need to know, and their next steps for learning.
When selecting an assessment task or tool, a teacher should consider:
- what they are seeking to learn about a student’s maths learning and whether the tool or task is fit for that purpose
- the assessment’s limitations and strengths. For example, many assessments measure accuracy or the ability to complete a task in a set time frame, but don’t show how a student is able to work flexibly to solve problems, which is key to being successful in maths.(49)
- how the task or tool fits with the schoolwide approach to progression steps and assessments – will it support discussions and information-sharing across the school, as well as knowledge about schoolwide achievement?
- their own confidence and capability to administer the assessment in a way that will gain an accurate assessment of a student’s learning or progress
- how they will provide feedback to the student’s to help them celebrate progress, learn, and improve
- how they might maximise the assessment information within the tool – what additional information could be gained from the assessment results?
- the setting in which the assessment is undertaken – how does it support the student to engage and succeed in demonstrating what they know?
- how the assessment itself could impact on the students’ experience and engagement in maths.
- whether the student will be able to use the tool or task to demonstrate their mathematical ability and knowledge. For example – are learning needs or disabilities being considered? Is it easy for a student to understand the instructions, the task or the language used? Is the cultural context of the problem familiar to them? Are they able to use equipment to support their thinking? How will their responses be captured if they have difficulty writing or communicating?
Real-life strategies
|
We heard from teachers and school leaders that it works well to… |
|
Use records of progress, modelling books, and photographs to monitor maths learning. Teachers use a variety of records to monitor and show progress, including: individual learning plans, digital learning platforms, videos, photographs, and modelling books from group teaching sessions. In some cases, modelling books or charts are used to inform reports on learning for parents. These are annotated by students or their teachers, and provide evidence of progress. |
|
Encourage students to explain their thinking when completing maths assessment tasks. When students talk about what they are thinking it gives teachers insights into their knowledge and understanding of maths concepts. At one school, teachers ask students about aspects of their approach to solving a problem, and record their ‘justification’ or description of their process. A teacher shared that monitoring students’ thinking through verbal discussion also removes additional pressure for some students: “It’s important that the [assessment] process allows them to access mathematical models and thinking without the additional challenge of having to read or write accurately.” |
|
Run assessments within the context of a planned maths lesson. In one school, tasks are set as an individualised task, and are closely monitored by the teacher. The student is given the materials they need and the question. The teacher checks they understand the task, and then the student gets to work. After a short time, the teacher returns and asks about aspects of their approach to solving the problem, and writes down their thinking to see how students got to those answers or records their ‘justification’ or description of their process, which helps the teacher understand how they are progressing in their learning. |
|
Work with other teachers to get familiar with the curriculum and progression frameworks. One larger school we spoke to keeps a relentless focus on all teachers knowing their school maths learning area well. Maths leaders spend dedicated time with teaching teams, supporting teachers to understand how to use progressions and implement aspects of the curriculum. “The more involved the teachers are, the more localised it is.” (School leader) |
|
Undertake regular moderation of assessments across the school. In one urban school, all teachers get together to plan and moderate assessment tasks as a group. This builds teachers’ capacity and confidence to make judgments in relation to curriculum progressions that are consistent across the school. Similar moderation sessions occur in a range of schools that we visited, often taking place several times a term. We heard that these hui are a valuable opportunity to clarify and reinforce teachers’ understandings about what each stage or level looks like. |
|
Work as a teacher team to build schoolwide maths expectations. In one school, teachers’ views on expected progress from Year 1 are gathered and aligned with other frameworks to develop their schoolwide expectation of maths progressions. This provides teachers with “the backbone of the curriculum plan, and they all know what they are doing, and how to adjust their teaching to the students.” (School leader) |
Informal and formal assessment
Informal assessment includes intentionally monitoring learning levels through discussion or observation. For example, teachers can encourage students to explain how they solved a problem and prompt students to make connections with a ‘big idea.’ They might purposefully observe students’ engagement levels during group work, a maths game, or set tasks. This sort of informal in-the-moment assessment not only shows students and teachers how well they are learning, but provide opportunities for further instruction and feedback that builds knowledge and addresses any misunderstandings.
Formal assessmentincludes planned assessments at the conclusion of a unit of work, teacher- or school-designed tests, or more formalised normed assessments such as Progressive Achievement Tests for Mathematics (PATs), Junior Assessment of Mathematics (JAM), and the Assessment Resource Banks (ARBs).
4) Good practice example
In one urban school with a high Māori and Pacific population, teachers integrate assessment into their classroom programme. They use ‘rapid routines’ activities to assess mathematical concepts and examine students’ knowledge, understandings, and strategies while students are solving problems. They undertake these in small collaborative groups where students work together and process their thinking out loud.
While groups work on their tasks, teachers observe, ask probing questions and encourage groups to explain their reasoning. Teachers also regularly use Progressive Achievement Tests (Mathematics) for Year 3 students (PATs), Junior Assessment of Mathematics (JAM), and the Assessment Resource Banks (ARBs). They also create adapted assessment tasks that suit students’ needs and the purpose. This includes providing timely feedback in the moment, affirming ideas specifically related to mathematical concepts and lesson learning outcomes, and looking for achievement against specific success criteria.
5) Reflective questions for teachers
- How do I find out what students already know and bring to the learning process, so that I can build on their current understandings?
- How can I provide opportunities for students to show what they know and celebrate their progress?
- How well do I understand my school’s learning progressions, and how concepts and maths processes are expected to develop as students progress through school? How do I use these to show students’ progress and determine next steps for learning?
- How do I know my students are progressing? What specific assessment tools are most useful in helping me to establish the rate of progress? How do I ensure I am using these tools accurately and effectively?
This practice area is about teachers purposefully building on their students’ experiences and knowledge to help them make progress in their maths learning. To do this, teachers draw on their maths content knowledge and understanding of maths learning progressions, to provide responsive teaching and assessment.
When this is going well, teachers understand what each student brings to their maths learning, what they already know, and what their next steps for learning are. They use this knowledge to inform their teaching and monitor progress.
In this section, we set out why teachers’ knowledge of students and their use of progressions and assessment information is so important for supporting students’ progress. We also offer practical guidance on how teachers can build this area of their own practice.
Overview of this section
This part of the report sets out useful information about how teachers can build and draw on their knowledge of maths progressions and assessments. It includes:
- What is this practice area?
- Why is this important?
- What does good practice look like in real life?
- Good practice example
- Reflective questions for teachers
1) What is this practice area?
This practice area is about teachers using their knowledge of students and about how maths concepts connect and build on each other, to line up learning experiences in a deliberate way. To do this, they purposefully find out what students know, and combine this with their knowledge about progressions. This information is used along with targeted assessment tasks and tools to identify what students know, how well they are progressing, and how teaching can best support their next learning steps. Teachers need to be explicit about what students should know and be able to do, so that they can develop specific goals with students.
The key teaching practices discussed in this section are:
- teachers determine what students bring to their learning, and build on what they already know
- teachers actively notice, recognise, and respond to students’ progress as they engage in maths
- teachers use assessment and progressions to plan for, document, and monitor students’ progress.
2) Why is this important?
When teachers are clear about what students know and bring to their maths learning, they can focus their teaching plans in response. Evidence shows that when teachers are confident about their role within their students’ maths learning journey, they raise their expectations for achievement and better target their teaching to promote progress.(43)
Teacher expectations make a difference
Teacher expectations impact significantly on students’ engagement and achievement.(44) This is an important consideration in the first few years of school when students are establishing views of themselves as students of maths and capable mathematicians.(45)
Teachers’ expectations are built on their understandings of how students current typically move along maths progression steps in relation to their cognitive development, and in relation to their school’s local maths curriculum. Getting really clear in these understandings helps teachers to hold useful expectations for learning and progress, and plan effective teaching in response.
It is important that teachers gain an in-depth awareness of their students’ understanding, so that they can respond in a timely and effective way to move them forward. In Years 1-3, students take time to develop maths knowledge through exposure to a variety of strategies and contexts,(46) so teachers need to constantly check on how these are developing. At a young age, assessment is best done in a natural setting, in the context of the everyday maths programme.(47) Deliberate selection of assessments and tasks can have a motivating effect, promoting positive student attitudes and a sense of accomplishment.
Good-quality assessment information provides a basis for planning next learning steps and adapting and targeting teaching – across the class and for individual students. Assessment helps teachers to set up expectations and goals for students, and plan purposeful learning steps which they can monitor to inform their decisions to move on. Assessing students’ understanding and knowledge also helps teachers adapt their practice and understand how effective it is in promoting the learning and progress of their students.
3) What does this area of practice look like in real life?
As part of this study, we talked to teachers and school leaders about the strategies that have worked well in their experience. We’ve collected their ideas and strategies here. It is important to reflect carefully about which of these will benefit each school’s unique community and context. No strategies are one-size-fits-all so all these strategies won’t be the right fit for everyone.
The key teacher practices that we focus on are:
- teachers determine what students bring to their learning, and build on what they already know
- teachers actively notice, recognise and respond to students’ progress as they engage in maths
- teachers use assessment and progressions to plan for, document, and monitor students’ progress.
a) Teachers determine what students bring to their learning, and build on what they already know
Teachers can assess what students already know through a variety of methods in a variety of contexts: from using formal assessment tools, to monitoring and observation during class. This will include providing a range of opportunities to learn about students’ prior experiences, attitudes, and strengths in maths. Assessment information should be used to inform next steps for teaching and what students should learn next.
Teaching that draws on the knowledge and skills students bring to school helps them see the relevance and practical uses of maths in their own lives. This includes building on students’ intuitive and existing understandings about maths.
Real-life strategies
|
We heard from teachers and school leaders that it works well to… |
|
Talk purposefully to students about their experiences, attitudes, and strengths in maths. Teachers find different opportunities throughout the day to hold informal conversations with their students that are focused on maths. This can occur as teachers set up for a maths session, as they interact during break times or in the playground, and as they engage in maths learning. Some opening questions to find out about their learning or experiences of maths include: Do you help with cooking at home? What games do you play together as a family? What is your favourite part of maths? What maths are you good at? What is the biggest/smallest number you know? |
|
Talk to colleagues about students’ prior experiences and progress in maths. Teachers talked to us about timely discussions held with teachers from previous classes to find out about their students’ previous experiences and successes in maths. They also learn from their colleagues in different year levels about what maths progress looks like for students in their classes. This helps them know where the students are coming from and heading towards in their maths journey. Schools involved in local clusters or Kāhui Ako use these networks to find out about what maths learning looks like, from early childhood education through to secondary school. |
|
Use diagnostic assessment to identify areas of strength and needs. This can be done through interviews with students, or setting an assessment task which focuses on familiarity a specific area of maths (e.g., a measurement task which can show student’s familiarity with measuring the weight or length of an object). Teachers use a range of assessments to gain insight into students’ knowledge, strategies, and understanding in a range of areas. |
|
Use an open task to assess student understanding. Teachers set an open task and observe how a student tackles the problem. This helps them to gauge the student’s level of competence in using expected knowledge, procedures, or skills. Selecting a task that can be approached in a range of different ways helps students to demonstrate their ability, and indicate what their next learning steps will be. Sometimes this is done through a summative assessment on a recent topic where students are given a problem that can be approached at any level of the curriculum. In one school, teachers come together as a team to link what students have done and pull out evidence from the national maths curriculum – and use this to identify what children have done or need to do to build on this. |
b) Teachers actively notice, recognise, and respond to students’ progress as they engage in maths
Targeted observation and effective questioning helps teachers understand what and how students are thinking and progressing. This equips them to provide purposeful instruction and feedback that builds on student knowledge and addresses any misunderstandings. When selecting a task, teachers should consider its level of challenge so that they can be ready to notice, recognise, and respond to what students demonstrate about their understanding and knowledge as they engage in that task.(48)
Effective questioning also helps teachers to learn about students’ prior experiences, attitudes, and strengths in maths. For example, a teacher can encourage students to explain how they solved a problem, and prompt the student to make connections with a ‘big idea’ that the class is currently focusing on.
Real-life strategies
|
We heard from teachers and school leaders that it works well to… |
|
Observe students’ engagement and be ready to respond. Teachers take note of the knowledge or processes a student relies on when they approach a task or respond to a question. Teachers note and respond to that student by: · adapting the task · adjusting the pace of the session · making a task simpler or more complex · demonstrating with or providing additional equipment · following up immediately with an individualised session · using this information in a subsequent group session. |
|
Check in with students through fast feedback techniques. Teachers we spoke with use a range of strategies to prompt students to assess their own levels of understanding or progress. This is done in formal and informal ways, for example: · students showing how well they understand a concept, how confident they feel, or how well they coped with a task by giving a thumbs up/down/hovering hand, or rating their understanding with one to five fingers · using emojis to show how they are feeling about their learning or understanding · encouraging students to talk with their peers about their learning. |
|
Participate in hands-on sessions with colleagues to uncover the underlying concepts in maths tasks and games. In one school, staff regularly work together to interact with equipment and collaborate on maths tasks. One school’s maths lead teacher reflected, “If you can’t solve it yourself, then you can’t expect the children to.” In these sessions, teachers discuss how their students might respond to the task, considering possible misconceptions and how they could pivot the lesson to address these. Teachers then work together to write these predictions up into a shared resource of ‘anticipations’ they can draw on. |
|
Listen to students to assess their understanding as they use equipment and talk to their peers. Several teachers talked about how they have learned to hold back from helping students when they are challenged to solve a maths task, in order to listen to their reasoning and watch them as they apply prior knowledge and manipulated materials. This helps teachers to identify current knowledge and any misconceptions or errors in their thinking, and to set new goals. |
c) Teachers use assessment and progressions to plan for, document, and monitor students’ progress
Effective teachers use systematic assessment and recording methods to monitor students’ progress and record their strategies and knowledge.
It’s important to keep in mind that assessment isn’t all about tests. In addition to normed or standardised assessments, early years maths can be assessed through purposeful task-setting, discussions with students, observations of group work, and more. (See the box below, for considerations when selecting assessment tools and tasks.) Teachers need a solid understanding of the range of formal and informal ways they can assess and monitor progress, to be able to make informed, timely teaching decisions.
Assessment decisions and records are most useful when teachers link them to their school’s curriculum and progression steps. In practice, this involves teachers using and recording assessment alongside the school’s expectations of progress. This helps teachers to monitor students’ progress, motivate students, and know about the effectiveness of their teaching.
Selecting assessment tools and tasks
The purpose of assessment is to provide clarity about what a student knows or has recently learnt, what they might need to know, and their next steps for learning.
When selecting an assessment task or tool, a teacher should consider:
- what they are seeking to learn about a student’s maths learning and whether the tool or task is fit for that purpose
- the assessment’s limitations and strengths. For example, many assessments measure accuracy or the ability to complete a task in a set time frame, but don’t show how a student is able to work flexibly to solve problems, which is key to being successful in maths.(49)
- how the task or tool fits with the schoolwide approach to progression steps and assessments – will it support discussions and information-sharing across the school, as well as knowledge about schoolwide achievement?
- their own confidence and capability to administer the assessment in a way that will gain an accurate assessment of a student’s learning or progress
- how they will provide feedback to the student’s to help them celebrate progress, learn, and improve
- how they might maximise the assessment information within the tool – what additional information could be gained from the assessment results?
- the setting in which the assessment is undertaken – how does it support the student to engage and succeed in demonstrating what they know?
- how the assessment itself could impact on the students’ experience and engagement in maths.
- whether the student will be able to use the tool or task to demonstrate their mathematical ability and knowledge. For example – are learning needs or disabilities being considered? Is it easy for a student to understand the instructions, the task or the language used? Is the cultural context of the problem familiar to them? Are they able to use equipment to support their thinking? How will their responses be captured if they have difficulty writing or communicating?
Real-life strategies
|
We heard from teachers and school leaders that it works well to… |
|
Use records of progress, modelling books, and photographs to monitor maths learning. Teachers use a variety of records to monitor and show progress, including: individual learning plans, digital learning platforms, videos, photographs, and modelling books from group teaching sessions. In some cases, modelling books or charts are used to inform reports on learning for parents. These are annotated by students or their teachers, and provide evidence of progress. |
|
Encourage students to explain their thinking when completing maths assessment tasks. When students talk about what they are thinking it gives teachers insights into their knowledge and understanding of maths concepts. At one school, teachers ask students about aspects of their approach to solving a problem, and record their ‘justification’ or description of their process. A teacher shared that monitoring students’ thinking through verbal discussion also removes additional pressure for some students: “It’s important that the [assessment] process allows them to access mathematical models and thinking without the additional challenge of having to read or write accurately.” |
|
Run assessments within the context of a planned maths lesson. In one school, tasks are set as an individualised task, and are closely monitored by the teacher. The student is given the materials they need and the question. The teacher checks they understand the task, and then the student gets to work. After a short time, the teacher returns and asks about aspects of their approach to solving the problem, and writes down their thinking to see how students got to those answers or records their ‘justification’ or description of their process, which helps the teacher understand how they are progressing in their learning. |
|
Work with other teachers to get familiar with the curriculum and progression frameworks. One larger school we spoke to keeps a relentless focus on all teachers knowing their school maths learning area well. Maths leaders spend dedicated time with teaching teams, supporting teachers to understand how to use progressions and implement aspects of the curriculum. “The more involved the teachers are, the more localised it is.” (School leader) |
|
Undertake regular moderation of assessments across the school. In one urban school, all teachers get together to plan and moderate assessment tasks as a group. This builds teachers’ capacity and confidence to make judgments in relation to curriculum progressions that are consistent across the school. Similar moderation sessions occur in a range of schools that we visited, often taking place several times a term. We heard that these hui are a valuable opportunity to clarify and reinforce teachers’ understandings about what each stage or level looks like. |
|
Work as a teacher team to build schoolwide maths expectations. In one school, teachers’ views on expected progress from Year 1 are gathered and aligned with other frameworks to develop their schoolwide expectation of maths progressions. This provides teachers with “the backbone of the curriculum plan, and they all know what they are doing, and how to adjust their teaching to the students.” (School leader) |
Informal and formal assessment
Informal assessment includes intentionally monitoring learning levels through discussion or observation. For example, teachers can encourage students to explain how they solved a problem and prompt students to make connections with a ‘big idea.’ They might purposefully observe students’ engagement levels during group work, a maths game, or set tasks. This sort of informal in-the-moment assessment not only shows students and teachers how well they are learning, but provide opportunities for further instruction and feedback that builds knowledge and addresses any misunderstandings.
Formal assessmentincludes planned assessments at the conclusion of a unit of work, teacher- or school-designed tests, or more formalised normed assessments such as Progressive Achievement Tests for Mathematics (PATs), Junior Assessment of Mathematics (JAM), and the Assessment Resource Banks (ARBs).
4) Good practice example
In one urban school with a high Māori and Pacific population, teachers integrate assessment into their classroom programme. They use ‘rapid routines’ activities to assess mathematical concepts and examine students’ knowledge, understandings, and strategies while students are solving problems. They undertake these in small collaborative groups where students work together and process their thinking out loud.
While groups work on their tasks, teachers observe, ask probing questions and encourage groups to explain their reasoning. Teachers also regularly use Progressive Achievement Tests (Mathematics) for Year 3 students (PATs), Junior Assessment of Mathematics (JAM), and the Assessment Resource Banks (ARBs). They also create adapted assessment tasks that suit students’ needs and the purpose. This includes providing timely feedback in the moment, affirming ideas specifically related to mathematical concepts and lesson learning outcomes, and looking for achievement against specific success criteria.
5) Reflective questions for teachers
- How do I find out what students already know and bring to the learning process, so that I can build on their current understandings?
- How can I provide opportunities for students to show what they know and celebrate their progress?
- How well do I understand my school’s learning progressions, and how concepts and maths processes are expected to develop as students progress through school? How do I use these to show students’ progress and determine next steps for learning?
- How do I know my students are progressing? What specific assessment tools are most useful in helping me to establish the rate of progress? How do I ensure I am using these tools accurately and effectively?
Practice area 2: Teachers use quality teaching practice in maths
This practice area is about ensuring effective teaching practices form the foundation for maths teaching practice.
When this is going well, teachers are able to effectively transfer teaching practices from other learning areas into a maths context. They are deliberate and intentional in their choice of approaches.
In this section, we set out why effective teaching strategies are important when teaching maths. We also offer practical guidance on how teachers can put this into practice in their own classrooms.
Overview of this section
This part of the report sets out useful information about how teachers use the key elements of effective teaching in the context of maths. It includes:
- What is this practice area?
- Why is this important?
- What does good practice look like in real life?
- Good practice example
- Reflective questions for teachers
1) What is this practice area?
This practice area is about ensuring that core teaching practices form the foundation for maths teaching practice. These practices are important for any curriculum area, but take on particular significance for maths contexts when working with young students. This means using deliberate, intentional teaching and organisational strategies that support students to focus, draw out their ideas, and progress their learning. Teachers will draw on good questioning skills and use timely, specific, and actionable feedback. They recognise when to support or extend students, when to move on to new learning, and when to spend longer on an area to consolidate learning for all students in their class.
The key teaching practices discussed in this section are:
- teachers provide scaffolding for students in maths
- teachers use explicit teaching in maths
- teachers use flexible grouping in maths
- teachers provide a range of cognitive and metacognitive strategies in maths.
2) Why is this important?
Teachers are not able to capably implement good maths-specific teaching practices without the basic ability to engage children in learning. Good quality general teaching skills like scaffolding, explicit teaching, flexible grouping, and cognitive and metacognitive strategies matter for maths, just as they do for other subject areas. Teachers who demonstrate good quality general teaching skills in other learning areas are well on the way to being effective teachers of maths.
3) What does good practice look like in real life?
As part of this study, we talked to teachers and school leaders about the strategies that have worked well in their experience. We’ve collected their ideas and strategies here. It is important to reflect carefully about which of these will benefit each school’s unique community and context. No strategies are one-size-fits-all so all these strategies won’t be the right fit for everyone.
The key teaching practices that we focus on are:
- teachers provide scaffolding for students in maths
- teachers use explicit teaching in maths
- teachers use flexible grouping in maths
- teachers provide a range of cognitive and metacognitive strategies in maths.
a) Teachers provide scaffolding for students in maths
Scaffolding helps students move from current understandings to new learning. In maths this is important as students engage with the developing complexities of maths over time. Teachers actively monitor students as they learn and look for ways to support their thinking. This is achieved through teacher questioning and prompts, as well as modelling of processes and worked examples, providing feedback, and supporting students with language and representations as they work through tasks.
"If you get stuck on things, she gives us something to help us like a pattern we know but we have forgotten about. She shows us a way to work it out [or] she might give us materials to help us." - Student
Real-life strategies
|
We heard from teachers and school leaders that it works well to… |
|
Gradually withdraw support or add complexity as students work through maths activities. For example, offering fewer instructions or prompts as students engage, and allowing students to make decisions about the approaches and representations to use when solving problems. A Year 3-4 teacher uses scaffolding to increase the difficulty of a skip-counting activity: the class sing a song called “Count by 4s”, which is designed to help memorise the 4x tables. Next, students sing the song to themselves, with a large piece of paper in front in case they get stuck – on the paper next to each number are its multiples of 4, e.g., 12 (3), 16 (4). In the next round, the teacher hides the paper. She then asks questions to the class, “How many 4s are in 64?” Following this, students complete 4x tables worksheets independently, writing them out as ‘families of facts’ equations. |
|
Prompt students to make links to maths knowledge and concepts from prior learning. For example, when students are sequencing two-digit numerals on cards, a teacher reminds students of the warm-up session when they had ordered numbers on a number line. |
|
Use questions or materials within group work to help students make connections. For example, a teacher working on addition and subtraction with a group of students asks: “What do you notice about these three groups of counters? What happens when you put them together? What else do you notice? What would happen if…? How is this different/the same as what we did yesterday?” |
b) Teachers use explicit teaching in maths
This is when teachers provide instruction to help students make sense of maths concepts, become more efficient in using maths strategies, or build their knowledge of maths procedures. Explicit maths teaching is about giving clear, concise instructions and support to help students know about the how and the why of critical maths skills, processes, and concepts.(50) This clarity supports students with the base understandings that they can draw from, for their more loosely-structured or play-based maths activities.
Explicit teaching in maths involves using worked examples and multiple applications to embed maths concepts for students and support them with clear frameworks for helping them to think about how to approach a problem and how to reflect on their learning. It might include modelling of multiple worked examples with clear supporting diagrams, guidance, and use of materials. Explicit teaching builds from teachers’ clear understanding of the whole school curriculum and an understanding of what progress should look like for students.
Real-life strategies
|
We heard from teachers and school leaders that it works well to… |
|
Focus closely on one particular maths procedure or skill in a maths session. For example, a teacher works with a small group to continue previous work on ordering numbers. “Remember we have been learning about the word ‘after’ like ‘after school’, ‘after playtime…’”. She gives examples of sentences previously used which connect with students’ lives: “After reading yesterday we went on a walk; After school, Anya went to visit her Nan… then we talked about lining up.” The teacher then arranges the five students in a line and asks them to turn and identify, “Who’s after you? Who’s before you?” They return to the table where the teacher writes numbers to 10 in a sequence directly on the tabletop. She uses a cut-out arrow to point to a number and then asks students to point to numbers that are directly ‘before’, and what comes ‘after’. Students then write the number themselves on the table with whiteboard pens. The students then each use number strips and put their finger on a number, then write the number that comes before, and after. They then continue this exercise on paper. |
|
Demonstrate to students how to solve a problem. This is done through deliberate teacher modelling - showing students how to approach a maths problem by breaking the task down and identifying each step. In one Year 2 class, a group of students are trying to count how many dots there are in a line using skip counting. The teacher is looking at the different ways her students solved this problem, and shares them so that the students can make connections and learn from each other: “[Student] saw that 4 and ‘1+1+1+1’ makes 8.” “[Student] skip counted groups of 2: 2, 4, 6, 8.” “[Student] saw that ‘3+3’ makes 6, and that ‘3 and 3’ and 2 makes 8!” The teacher then shows their thinking as diagrams and equations on the white board. |
c) Teachers use flexible grouping in maths
Young students benefit from working on maths tasks in a range of different group configurations.(51) Teachers ensure students have opportunities to work with maths tasks individually, in pairs, as a whole class, in self-selected or teacher-selected groups, and with peers that have a range of knowledge and skills. Teachers group students in various ways within a single lesson, depending on the task, existing social relationships, and the students’ needs.
The composition and size of the group is often determined by the teacher, and sometimes results in groups of students with a range of knowledge and skills. This exposes them to a range of different ideas and gives them opportunities to act as a student and as a teacher.
Real-life strategies
|
We heard from teachers and school leaders that it works well to… |
|
Organise students to work in a variety of groupings during a lesson. In a Year 2-3 class, teachers use a range of grouping sizes within one statistics-focused task. Students start off by working in pairs to create a graph, and then join with another pair to explain what their graph represents. Teachers prompt students to add to each other’s ideas and ask questions. Students also compare their different methods for solving the problem. For example, one pair used tally charts, and another counted in 5s. |
|
Monitor how students are supporting the learning of others. For example, a teacher sets students up to work in pairs or small groups on a task. The teacher then observes the groups as they begin to approach the task, watching for signs of a lack of confidence or focus. They move from group to group listening to how specific students are engaging, and reminds students about how to share and respond to others’ ideas. The teacher asks specific students to explain their process to others or show peers how they are using equipment, working as tuakana/teina[1] to support each other. |
|
Differentiate learning within a shared task. For example, providing a task for a group of students that involves choosing numbers within different ranges, or using different operations. An example is set out below. Make up a problem that has the number 24 as the answer: · by using numbers between 0 and 20; 20 – 100; using 3-digit numerals; using decimals or fractions · by using addition, subtraction, multiplication, or division – or all 4 operations
In classes, we observed teachers offering opportunities for students to access activities or play a game which fitted their current level of knowledge or competence, for example: “Use the 2-digit numbers, or if you feel confident, use the 3-digit numbers to play the game”. |
Note: The tuakana–teina relationship, an integral part of traditional Māori society, provides a model for buddy systems. An older or more expert tuakana (brother, sister, or cousin) helps and guides a younger or less expert teina (originally a younger sibling or cousin of the same gender). From Te reo Maori in English-medium schools, Te Kete Ipurangi.
“By having mixed ability, you expose students to all ideas. For example, a student can think deeply, even though she doesn’t know what ‘8’ looks like. By exposing her to all these ideas, she hears all the things happening around her, which benefits her in the long term.” (Teacher)
d) Teachers provide a range of cognitive and metacognitive strategies in maths
Teachers can help students to explain their thinking processes and strategies during tasks. ‘Cognitive strategies’ help students to tackle problems effectively by giving them a structure or thinking tools, such as concepts maps or guides, to support learning when a task cannot be completed through a simple series of steps. ‘Metacognitive strategies’ help them to think how they approach a problem and how they learn. They also help them review and understand how they get an answer to a maths problem, even if it's wrong.
Teachers can purposefully promote these skills by asking questions and prompting students to approach maths problems in a deliberate and logical way (applying cognitive strategies), and to reflect on and understand how they approached it and how well that worked (applying metacognitive awareness). These are useful learning skills that can be transferred to new contexts and problems. These strategies also help the teacher to understand what the student knows and how confident they feel in approaching the task.
Real-life strategies
|
We heard from teachers and school leaders that it works well to… |
|
Use questions to encourage students to think out loud as they work with a maths task, and explain their thinking to others. In one Year 1-2 class, a teacher prompts a student to explain how he solved a problem, asking, “How did you work that out?” The student explains “I counted in 2s, then I counted in 3s.” and the teacher prompts: “Tell us how it made 8.” The student circles patterns on a photo. He shows how he saw 3+3 (writes it) and the teacher then asks the class: “Do you know something about 3+3?” Student: “It’s 6!” |
|
Use structured frameworks to help students access and practice ideas. For example, a teacher includes steps and prompts with a maths problem that helps a group of students work through the problem and find success. (See the box below for an example of a structured framework.) |
|
Provide opportunities for students to revisit and reflect on their learning or progress in maths. For example, at the end of the session a teacher prompts students to talk to a buddy about something they learned to do in maths today, or a difficulty they had and how they solved it. She asks, “What was the thing that most helped you?” The teacher sometimes asks students to write a reflection about their learning, e.g., a statement about their progress or their confidence in doing subtraction with 2-digit numbers. |
Example: A structured framework to encourage students’ cognitive strategies
- Reading the problem. The student reads the problem carefully, noting and attempting to clear up any areas of uncertainty or confusion (e.g., unknown vocabulary terms).
- Paraphrasing the problem. The student restates the problem in their own words.
- ‘Drawing’ the problem. The student creates a drawing of the problem, creating a visual representation of the word problem.
- Creating a plan to solve the problem. The student decides on the best way to solve the problem and develops a plan to do so.
- Predicting/Estimating the answer. The student estimates or predicts what the answer to the problem will be. The student may compute a quick approximation of the answer, using rounding or other shortcuts.
- Computing the answer. The student follows the plan developed earlier to compute the answer to the problem.
- Checking the answer. The student methodically checks the calculations for each step of the problem. The student also compares the actual answer to the estimated answer calculated in a previous step to ensure that there is general agreement between the two values.(52)
4) Good practice example
A Year 1 teacher supports students to talk aloud about their thinking and reasoning, as they work through the explicit teaching of a multiplication task.
A photograph of eight dice arranged in a pattern is presented to students on a large screen. The teacher asks students to explain how many dots they see using the phrase, “I notice that…” Then the rest of the class is asked whether they “agree” or “disagree.” Each student has a different way of identifying the number of dots by picking up on different patterns. The teacher then prompts some students to explain why they agreed or disagreed. This develops into a thoughtful class discussion, with students practising maths vocabulary connected to multiplication and addition (‘skip-count’, ‘lots of’, ‘groups of’, ‘plus’, ‘times’, etc.). This is enabled by a supportive classroom environment and culture which encourages risk-taking by students.
5) Reflective questions for teachers
- What parts of my teaching get the best response out of my students?
- Which good-quality teaching skills that I use in other learning areas can I apply more often in maths time?
- Do I make clear connections between what students are learning now and prior learning?
- How can I better organise for learning and group my students more effectively? What is the best group size and mix of students’ knowledge and skills for this particular activity?
- How can I differentiate my teaching more for my students to ensure it supports them to engage more fully and progress?
- How do I encourage my students to think about their learning? What strategies do I find most useful for helping students reflect on and share their learning?
This practice area is about ensuring effective teaching practices form the foundation for maths teaching practice.
When this is going well, teachers are able to effectively transfer teaching practices from other learning areas into a maths context. They are deliberate and intentional in their choice of approaches.
In this section, we set out why effective teaching strategies are important when teaching maths. We also offer practical guidance on how teachers can put this into practice in their own classrooms.
Overview of this section
This part of the report sets out useful information about how teachers use the key elements of effective teaching in the context of maths. It includes:
- What is this practice area?
- Why is this important?
- What does good practice look like in real life?
- Good practice example
- Reflective questions for teachers
1) What is this practice area?
This practice area is about ensuring that core teaching practices form the foundation for maths teaching practice. These practices are important for any curriculum area, but take on particular significance for maths contexts when working with young students. This means using deliberate, intentional teaching and organisational strategies that support students to focus, draw out their ideas, and progress their learning. Teachers will draw on good questioning skills and use timely, specific, and actionable feedback. They recognise when to support or extend students, when to move on to new learning, and when to spend longer on an area to consolidate learning for all students in their class.
The key teaching practices discussed in this section are:
- teachers provide scaffolding for students in maths
- teachers use explicit teaching in maths
- teachers use flexible grouping in maths
- teachers provide a range of cognitive and metacognitive strategies in maths.
2) Why is this important?
Teachers are not able to capably implement good maths-specific teaching practices without the basic ability to engage children in learning. Good quality general teaching skills like scaffolding, explicit teaching, flexible grouping, and cognitive and metacognitive strategies matter for maths, just as they do for other subject areas. Teachers who demonstrate good quality general teaching skills in other learning areas are well on the way to being effective teachers of maths.
3) What does good practice look like in real life?
As part of this study, we talked to teachers and school leaders about the strategies that have worked well in their experience. We’ve collected their ideas and strategies here. It is important to reflect carefully about which of these will benefit each school’s unique community and context. No strategies are one-size-fits-all so all these strategies won’t be the right fit for everyone.
The key teaching practices that we focus on are:
- teachers provide scaffolding for students in maths
- teachers use explicit teaching in maths
- teachers use flexible grouping in maths
- teachers provide a range of cognitive and metacognitive strategies in maths.
a) Teachers provide scaffolding for students in maths
Scaffolding helps students move from current understandings to new learning. In maths this is important as students engage with the developing complexities of maths over time. Teachers actively monitor students as they learn and look for ways to support their thinking. This is achieved through teacher questioning and prompts, as well as modelling of processes and worked examples, providing feedback, and supporting students with language and representations as they work through tasks.
"If you get stuck on things, she gives us something to help us like a pattern we know but we have forgotten about. She shows us a way to work it out [or] she might give us materials to help us." - Student
Real-life strategies
|
We heard from teachers and school leaders that it works well to… |
|
Gradually withdraw support or add complexity as students work through maths activities. For example, offering fewer instructions or prompts as students engage, and allowing students to make decisions about the approaches and representations to use when solving problems. A Year 3-4 teacher uses scaffolding to increase the difficulty of a skip-counting activity: the class sing a song called “Count by 4s”, which is designed to help memorise the 4x tables. Next, students sing the song to themselves, with a large piece of paper in front in case they get stuck – on the paper next to each number are its multiples of 4, e.g., 12 (3), 16 (4). In the next round, the teacher hides the paper. She then asks questions to the class, “How many 4s are in 64?” Following this, students complete 4x tables worksheets independently, writing them out as ‘families of facts’ equations. |
|
Prompt students to make links to maths knowledge and concepts from prior learning. For example, when students are sequencing two-digit numerals on cards, a teacher reminds students of the warm-up session when they had ordered numbers on a number line. |
|
Use questions or materials within group work to help students make connections. For example, a teacher working on addition and subtraction with a group of students asks: “What do you notice about these three groups of counters? What happens when you put them together? What else do you notice? What would happen if…? How is this different/the same as what we did yesterday?” |
b) Teachers use explicit teaching in maths
This is when teachers provide instruction to help students make sense of maths concepts, become more efficient in using maths strategies, or build their knowledge of maths procedures. Explicit maths teaching is about giving clear, concise instructions and support to help students know about the how and the why of critical maths skills, processes, and concepts.(50) This clarity supports students with the base understandings that they can draw from, for their more loosely-structured or play-based maths activities.
Explicit teaching in maths involves using worked examples and multiple applications to embed maths concepts for students and support them with clear frameworks for helping them to think about how to approach a problem and how to reflect on their learning. It might include modelling of multiple worked examples with clear supporting diagrams, guidance, and use of materials. Explicit teaching builds from teachers’ clear understanding of the whole school curriculum and an understanding of what progress should look like for students.
Real-life strategies
|
We heard from teachers and school leaders that it works well to… |
|
Focus closely on one particular maths procedure or skill in a maths session. For example, a teacher works with a small group to continue previous work on ordering numbers. “Remember we have been learning about the word ‘after’ like ‘after school’, ‘after playtime…’”. She gives examples of sentences previously used which connect with students’ lives: “After reading yesterday we went on a walk; After school, Anya went to visit her Nan… then we talked about lining up.” The teacher then arranges the five students in a line and asks them to turn and identify, “Who’s after you? Who’s before you?” They return to the table where the teacher writes numbers to 10 in a sequence directly on the tabletop. She uses a cut-out arrow to point to a number and then asks students to point to numbers that are directly ‘before’, and what comes ‘after’. Students then write the number themselves on the table with whiteboard pens. The students then each use number strips and put their finger on a number, then write the number that comes before, and after. They then continue this exercise on paper. |
|
Demonstrate to students how to solve a problem. This is done through deliberate teacher modelling - showing students how to approach a maths problem by breaking the task down and identifying each step. In one Year 2 class, a group of students are trying to count how many dots there are in a line using skip counting. The teacher is looking at the different ways her students solved this problem, and shares them so that the students can make connections and learn from each other: “[Student] saw that 4 and ‘1+1+1+1’ makes 8.” “[Student] skip counted groups of 2: 2, 4, 6, 8.” “[Student] saw that ‘3+3’ makes 6, and that ‘3 and 3’ and 2 makes 8!” The teacher then shows their thinking as diagrams and equations on the white board. |
c) Teachers use flexible grouping in maths
Young students benefit from working on maths tasks in a range of different group configurations.(51) Teachers ensure students have opportunities to work with maths tasks individually, in pairs, as a whole class, in self-selected or teacher-selected groups, and with peers that have a range of knowledge and skills. Teachers group students in various ways within a single lesson, depending on the task, existing social relationships, and the students’ needs.
The composition and size of the group is often determined by the teacher, and sometimes results in groups of students with a range of knowledge and skills. This exposes them to a range of different ideas and gives them opportunities to act as a student and as a teacher.
Real-life strategies
|
We heard from teachers and school leaders that it works well to… |
|
Organise students to work in a variety of groupings during a lesson. In a Year 2-3 class, teachers use a range of grouping sizes within one statistics-focused task. Students start off by working in pairs to create a graph, and then join with another pair to explain what their graph represents. Teachers prompt students to add to each other’s ideas and ask questions. Students also compare their different methods for solving the problem. For example, one pair used tally charts, and another counted in 5s. |
|
Monitor how students are supporting the learning of others. For example, a teacher sets students up to work in pairs or small groups on a task. The teacher then observes the groups as they begin to approach the task, watching for signs of a lack of confidence or focus. They move from group to group listening to how specific students are engaging, and reminds students about how to share and respond to others’ ideas. The teacher asks specific students to explain their process to others or show peers how they are using equipment, working as tuakana/teina[1] to support each other. |
|
Differentiate learning within a shared task. For example, providing a task for a group of students that involves choosing numbers within different ranges, or using different operations. An example is set out below. Make up a problem that has the number 24 as the answer: · by using numbers between 0 and 20; 20 – 100; using 3-digit numerals; using decimals or fractions · by using addition, subtraction, multiplication, or division – or all 4 operations
In classes, we observed teachers offering opportunities for students to access activities or play a game which fitted their current level of knowledge or competence, for example: “Use the 2-digit numbers, or if you feel confident, use the 3-digit numbers to play the game”. |
Note: The tuakana–teina relationship, an integral part of traditional Māori society, provides a model for buddy systems. An older or more expert tuakana (brother, sister, or cousin) helps and guides a younger or less expert teina (originally a younger sibling or cousin of the same gender). From Te reo Maori in English-medium schools, Te Kete Ipurangi.
“By having mixed ability, you expose students to all ideas. For example, a student can think deeply, even though she doesn’t know what ‘8’ looks like. By exposing her to all these ideas, she hears all the things happening around her, which benefits her in the long term.” (Teacher)
d) Teachers provide a range of cognitive and metacognitive strategies in maths
Teachers can help students to explain their thinking processes and strategies during tasks. ‘Cognitive strategies’ help students to tackle problems effectively by giving them a structure or thinking tools, such as concepts maps or guides, to support learning when a task cannot be completed through a simple series of steps. ‘Metacognitive strategies’ help them to think how they approach a problem and how they learn. They also help them review and understand how they get an answer to a maths problem, even if it's wrong.
Teachers can purposefully promote these skills by asking questions and prompting students to approach maths problems in a deliberate and logical way (applying cognitive strategies), and to reflect on and understand how they approached it and how well that worked (applying metacognitive awareness). These are useful learning skills that can be transferred to new contexts and problems. These strategies also help the teacher to understand what the student knows and how confident they feel in approaching the task.
Real-life strategies
|
We heard from teachers and school leaders that it works well to… |
|
Use questions to encourage students to think out loud as they work with a maths task, and explain their thinking to others. In one Year 1-2 class, a teacher prompts a student to explain how he solved a problem, asking, “How did you work that out?” The student explains “I counted in 2s, then I counted in 3s.” and the teacher prompts: “Tell us how it made 8.” The student circles patterns on a photo. He shows how he saw 3+3 (writes it) and the teacher then asks the class: “Do you know something about 3+3?” Student: “It’s 6!” |
|
Use structured frameworks to help students access and practice ideas. For example, a teacher includes steps and prompts with a maths problem that helps a group of students work through the problem and find success. (See the box below for an example of a structured framework.) |
|
Provide opportunities for students to revisit and reflect on their learning or progress in maths. For example, at the end of the session a teacher prompts students to talk to a buddy about something they learned to do in maths today, or a difficulty they had and how they solved it. She asks, “What was the thing that most helped you?” The teacher sometimes asks students to write a reflection about their learning, e.g., a statement about their progress or their confidence in doing subtraction with 2-digit numbers. |
Example: A structured framework to encourage students’ cognitive strategies
- Reading the problem. The student reads the problem carefully, noting and attempting to clear up any areas of uncertainty or confusion (e.g., unknown vocabulary terms).
- Paraphrasing the problem. The student restates the problem in their own words.
- ‘Drawing’ the problem. The student creates a drawing of the problem, creating a visual representation of the word problem.
- Creating a plan to solve the problem. The student decides on the best way to solve the problem and develops a plan to do so.
- Predicting/Estimating the answer. The student estimates or predicts what the answer to the problem will be. The student may compute a quick approximation of the answer, using rounding or other shortcuts.
- Computing the answer. The student follows the plan developed earlier to compute the answer to the problem.
- Checking the answer. The student methodically checks the calculations for each step of the problem. The student also compares the actual answer to the estimated answer calculated in a previous step to ensure that there is general agreement between the two values.(52)
4) Good practice example
A Year 1 teacher supports students to talk aloud about their thinking and reasoning, as they work through the explicit teaching of a multiplication task.
A photograph of eight dice arranged in a pattern is presented to students on a large screen. The teacher asks students to explain how many dots they see using the phrase, “I notice that…” Then the rest of the class is asked whether they “agree” or “disagree.” Each student has a different way of identifying the number of dots by picking up on different patterns. The teacher then prompts some students to explain why they agreed or disagreed. This develops into a thoughtful class discussion, with students practising maths vocabulary connected to multiplication and addition (‘skip-count’, ‘lots of’, ‘groups of’, ‘plus’, ‘times’, etc.). This is enabled by a supportive classroom environment and culture which encourages risk-taking by students.
5) Reflective questions for teachers
- What parts of my teaching get the best response out of my students?
- Which good-quality teaching skills that I use in other learning areas can I apply more often in maths time?
- Do I make clear connections between what students are learning now and prior learning?
- How can I better organise for learning and group my students more effectively? What is the best group size and mix of students’ knowledge and skills for this particular activity?
- How can I differentiate my teaching more for my students to ensure it supports them to engage more fully and progress?
- How do I encourage my students to think about their learning? What strategies do I find most useful for helping students reflect on and share their learning?
Practice area 3: Teachers provide dedicated maths time every day so all students engage meaningfully in learning
This practice area is about teachers ensuring they timetable, plan for, and implement focused maths time each day. Maths sessions should be varied and engaging. This ensures that students are well-supported to learn, practise, and apply maths.
When this is going well, teachers take a deliberate approach to providing new and revisited maths learning. They encourage students to clarify their ideas, make connections, and continually build their knowledge and skills.
In this section, we set out why providing dedicated, quality maths time each day is important for students. We also offer practical guidance on how teachers can put this into practice in their own classrooms.
Overview of this section
This part of the report sets out useful information about how teachers provide dedicated maths time. It includes:
- What is this practice area?
- Why is this important?
- What does good practice look like in real life?
- Good practice example
- Reflective questions for teachers
1) What is this practice area?
“We really like to do maths, that’s why we do it every day!” - Student
This practice area is about providing daily opportunities to learn and practise maths. Daily maths should be timetabled, purposeful, and sequenced in a way that builds on existing knowledge and prepares students for further complexity. Within the time that is dedicated to maths, every effort should be made to maximise the time spent learning.
Quality daily maths involves a deliberate mix of:
- explicit instruction or opportunities to build new concepts and skills
- individual, pair, or group tasks that support students to practise new concepts and skills
- problem-based learning and more open-ended maths tasks and games that promote their interest, encourage critical thinking through wondering and questioning, and provide discussion opportunities to help teachers see how students are going and where to focus next.
Maths time should follow a clear structure, usually with a predictable motivating start followed by work time which may include group, individual, pair, or class experiences. Lessons should end with an opportunity to make connections and reflect on the learning. Sessions work best when they are designed to fully engage and include all students, helping them to build understandings and make connections to their world.
The key teaching practices discussed in this section are:
- teachers support students to learn, practise, create, and use maths daily
- teachers show students how to use maths procedures and skills accurately, efficiently, and flexibly
- teachers prompt students to talk about their maths ideas
- teachers provide cognitively challenging mathematics activities.
2) Why is this important?
Focused daily maths time is needed for students to develop their foundational maths skills and knowledge. Studies show that students achieve better in maths when they have daily exposure to maths instruction, time to practice, and opportunities for application and critical thinking.(53) At this early stage of their maths journey, it is important that young students have sufficient time to interact with and familiarise with maths concepts. This involves providing students with learning experiences at a pace that challenges them and supports their continued progress. This sets them up for positive engagement and further learning in maths: a pathway to a wide range of learning opportunities, activities, and occupations.
“Time allocated [for maths] sets the outside boundaries for what it is possible to learn. While mathematics and statistics can and should be integrated with other learning areas, setting aside focused learning time each day will provide space for increased engagement with mathematics.”
- Royal Society, 2021(54)
“Routine and structure are important to kids.” - Teacher
3) What does good practice look like in real life?
As part of this study, we talked to teachers and school leaders about the strategies that have worked well in their experience. We’ve collected their ideas and strategies here. It is important to reflect carefully about which of these will benefit each school’s unique community and context. No strategies are one-size-fits-all so all these strategies won’t be the right fit for everyone.
The key teacher practices that we focus on are:
- teachers support students to learn, practise, create, and use maths daily
- teachers show students how to use maths procedures and skills accurately, efficiently, and flexibly
- teachers prompt students to talk about their maths ideas
- teachers provide cognitively challenging maths activities.
a) Teachers support students to learn, practise, create, and use maths daily
It is more effective for students when daily maths sessions are planned out to ensure that they encounter a variety of activities. These should help students experience the breadth and depth of maths, and to learn, consolidate, and apply maths ideas. This can be done in a range of ways, but the key is to have a deliberate mix of instruction, practice, and exploration. Maths time can incorporate a selection of:
- whole-class, group, and individual tasks that revisit and practice skills and knowledge
- instructional sessions
- maths games
- problem-based learning, including complex problems
- conversations about maths
- real-world, hands-on tasks.
Problem based learning supports children’s active participation in the process of solving mathematical problems from the outset. It fosters collaborative learning, encourages knowledge retention and conceptual development, a positive attitude towards mathematics and leads to higher mathematical gains.
- O’Neill et al., 2023(55)
“Maths games are for learning and having fun at the same time.” – Student
Real-life strategies
|
We heard from teachers and school leaders that it works well to… |
|
Carefully consider the timing of maths sessions and content. Leaders and teachers in one school spoke about how they review their approach to maths across the junior school. They put strategies in place to ensure there is a consistent approach to prioritising and implementing maths. This includes a schoolwide discussion on maths topics, followed by planning sessions in the syndicate, with a strong focus on unpacking maths concepts. To strengthen their focus on maths, teachers at one school have established a consistent ‘maths time’ at the start of each day – the time that they had noticed students are most engaged. All teachers work through agreed content, and undertake assessments at the same time at the end of a unit. In their review, they had also recognised that the areas of weakest performance (e.g. fractions) were being taught later in the year. To remedy this, fractions is now taught at the start of the year, for more focus and stronger effort. |
|
Use whole-class warm-up activities. Teachers begin maths sessions through revisiting prior learning experiences by using familiar routines, practices, or equipment. These activities are an opportunity to repeat, revise, and extend on the maths ideas in focus. For example, we observed a warm-up activity called ‘Guess the number’, where students are asked to guess a number chosen by the teacher using a process of elimination with the hundreds-board as reference. Students asked questions like: “Is it bigger than 50?” “Is it an odd number?” and “Is it in the 6th row?” – to which the teacher responded, “Do you mean the 60s row, or in the 6th column?” Teachers shared that a benefit of whole-class activities is that all students in the class are exposed to ideas and concepts and can participate. Even if some are not fully confident in what they are doing, they will be exposed to ideas and concepts and be able to learn from their peers. For example, a student may only be confident counting to 20, yet a warm-up activity will include the whole class counting together to 100 using a hundreds-board. |
|
Use a ‘number of the day’ to frame discussions of maths concepts. Many of the schools we talked to use this strategy. For example, in one class the number 42 is introduced as the ‘number of the day’ in the warm-up activity. The teacher asks students: · What is it? (e.g., number 42) · What numbers come before/after? · What number is less/more? · How do you spell it? · What is 42 + [random numbers] · Partition 42 using place value · Round 42 to the nearest 10 · Arrange the random numbers (including 42) in ascending order. |
|
Choose active or hands-on activities for practising new learning. In one Year 1 class, students are given a number from 0-10 and line up in the correct order to make a human number-line.
|
|
Offer a range of difficulty options. In one classroom we visited, the teacher offers students a choice of activities which range in difficulty from ‘mild’ (easy), to ‘medium’, to ‘hot’ (more difficult). Students choose the level of challenge. The teacher shared that she monitors the difficulty levels being selected as part of her informal formative assessment of students’ confidence, and notes what areas of learning need extra attention. The teacher has noted that this activity supports confidence and motivation in the class: being able to complete an activity independently, no matter the difficulty level, encourages students to feel confident and successful. |
b) Teachers show students how to use maths procedures and skills accurately, efficiently, and flexibly
Teachers need to provide multiple opportunities for students to build up their toolkit of strategies (flexible ways to solve a problem) and procedures for solving maths problems. These need to be based on good understandings of the strategies, rather than following rigid, step-by-step processes or learning a set of rules.
“When students use a procedure they do not understand, they are more likely to make errors and fail to notice when the answer does not make sense.”
- National Council of Teachers of Mathematics, 2023(56)
In practice, this means that teachers need to provide opportunities for students to learn new strategies and procedures, practise using them so that they become proficient, and apply them confidently in a range of contexts. This includes supporting students to make connections between strategies.
Understanding is much more valuable than memorisation
When teachers focus on helping students memorise maths facts or procedures without understanding them, they are not supporting students in the long term. Memorising a rigid set of rules or reciting rote-learning alone without other methods of teaching those concepts may help students get answers correct in Years 1-3, but won’t provide the solid grounding of understanding that is needed for the next parts of those students’ maths journeys.
For example, basic facts can be taught using number relationships and reasoning strategies, not memorisation. A 10s frame which shows 7 counters helps students to see what 7 looks like (and how it mirrors how they show 7 with their hands). It also illustrates basic facts such as 5+2=7, 7-5=2 as well as 10-7=3, 7+3=10 . This understanding helps students to start building strategies beyond basic facts too – such as ‘making a whole’ with fractions and decimals – 7/10, .7 etc.
Real-life strategies
|
We heard from teachers and school leaders that it works well to… |
|
Provide repeated opportunities to encounter and practise ideas through a range of contexts, activities, and equipment. For example, the teacher uses both the hundreds-board and number blocks to teach the students to count in 10s. The teacher incorporates repetition into a warm-up activity to practise prior learning (e.g., counting together on the hundreds-board, counting in 5s on the abacus), or part of scaffolding a new skill (e.g., learning the 4x tables). Repetition of counting sequences, patterns, and basic knowledge helps students to memorise and recognise them. |
|
Set tasks that deliberately link to students’ experiences or interests. For example, the teacher introduces a problem where students imagine they are at a birthday party, and need to partition the birthday cake into 8 equal pieces. The students must figure out the best strategy to do this. This problem gets students thinking about different maths procedures, including division (dividing a whole to make 8) and multiplication (multiply the number of pieces to make 8). During the lesson, the teacher actively reminds students of how these link to strategies or knowledge recently covered. |
|
Use carefully selected maths games for introducing and practising maths ideas. We observed classes where the use of maths games is an important part of maths time. In one class, tables are set out with selected games, aligned to the teaching focus. The purpose of the games is clearly identified on a card with the instructions and students make a record of what they are doing. Teachers we spoke with promote maths games that are sometimes physical (e.g., a board game or something that uses materials) or digital (e.g., on an iPad). Games are played in whole-class or group settings, often independent of the teacher. Teachers shared that they purposefully select specific games to link to current or recent maths learning. They also consider whether the games can generate sharing and discussion of ideas among students, and whether they will offer sufficient challenge while still being accessible. |
“When we go on the mat for learning, I like doing graphs and tally marks. I love how they add up together.” - Student
c)Teachers prompt students to talk about their maths ideas
Engaging in ‘maths’ talk helps students to think critically and make sense of their own and others’ ideas. It also supports teachers to monitor students’ accuracy and complexity of maths thinking. That way, they can quickly respond to any misunderstandings that need to be corrected.
In practice, teachers have a key role in questioning students as well as creating a classroom which is full of maths discussion. This can be done by creating regular opportunities for conversations about mathematical ideas with individuals or small groups. Teachers might encourage students to ask questions, explain why they have come to a particular answer, or why they agree or disagree with others’ ideas. Mutual respect and high expectations from the teacher are crucial for students to feel confident in contributing their thoughts and engaging with their peers’ ideas.
Real-life strategies
|
We heard from teachers and school leaders that it works well to… |
|
Focus on developing students’ use of mathematical language and vocabulary. This equips students for discussions about their maths thinking. For example, one teacher introduces specific maths vocabulary during maths time and encourages students to use these words when explaining their answers to maths problems. The teacher also uses warm-up activities like counting together to reinforce ideas, such as the difference between ‘ty’ (i.e., thirty) and ‘teen’ (i.e., thirteen). When counting together using a hundreds-board for example, students are encouraged to loudly emphasise these sounds as a way of committing them to memory. |
|
Encourage students to describe their thinking. This helps students to explain their thinking and how they solved a problem. For example, a teacher prompts students with questions like, “Why do you think that?” and “Can you explain to your classmates how you got that answer?” This encourages students to explain their thinking in their own words and practice using the maths language that they have been learning (e.g., words like “probably” and “because”). The intent of this strategy is to get the student to think about the approach they used to solve a problem, and to share this with other students. |
|
Use questioning and prompts to guide students as they attempt to solve a maths problem. The teacher guides students to use a particular approach, asking, “What would happen if you tried…” If an answer is incorrect, the teacher asks questions to prompt them to reassess their answer and their approach, using phrases like, “Why do you think that?” or “Tell me about how you came up with this answer.” |
|
Explicitly teach maths words, and talk about the connections between them. As part of a lesson in statistics, one teacher asks her mixed class of Year 1s and 2s if anyone can explain the meaning of the word ‘probability’. Some students respond using words they had learnt previously: ‘possibly’ and ‘probably’. The teacher had taught these students to use accompanying hand gestures:
The class’s understanding of these similar mathematical words paves the way for their understanding of the new term ‘probability’. |
|
Use what one student says to prompt wider discussion. For example, a teacher presents a maths problem and asks a student to explain how they reached their answer. This is sometimes referred to as ‘justifying’ their answer. The student’s answer is used to prompt reactions from other students – “Do you agree or disagree? Why?” |
d) Teachers provide cognitively challenging maths activities
Students benefit from maths tasks that make them engage in maths thinking where the answer is not obvious. This is often done through presenting maths problems to solve (either real-life or imagined) which take time and may require support from equipment, visual representations, and prompts from the teacher. These sorts of tasks, sometimes called ‘challenging tasks’, or ‘rich tasks’,(57) offer all students the opportunity to participate and be stretched.
“All students [should be] working on ‘worthwhile, challenging tasks conducive to productive struggle’ (effortful learning requiring reasoning, problem solving, and perseverance).” - Ministry of Education, 2022(58)
“Children’s mana and self-esteem is uplifted when they can solve problems themselves.” - Teacher
Real-life strategies
|
We heard from teachers and school leaders that it works well to… |
|
Use photographs as prompts for complex peer discussions. In one class, students are asked to predict from a series of photographs: “How many glass beads in the jar?” and “How many now?” when the number of beads increase. Students share what they think with their partner and share back with the larger group. The teacher responds by drawing out their thinking, illustrating with diagrams or equations, and building on what they offer.
|
|
Ask questions with lots of possible answers or approaches. For example, in the context of measurement, looking at area and perimeter concepts: “Draw some letters of the alphabet on squared paper using exactly 10 squares” or “Using equipment or symbols, show five different ways of showing the number 15.” This task has endless solutions, and can support students who are just beginning to understand how many 15 is, what it looks like with different kinds of equipment and representation, or where it falls in a counting sequence, as well as those who are able to represent 15 as 3 times 5, or a quarter of 60, or 340 – 325, 10 times bigger than 1.5, etc. In a Year 1-2 class, a group of mixed-ability students are required to split a cake represented by a piece of paper into four parts. Confident students fold the paper over twice to ensure all parts are equal, and less confident students manually draw lines across the paper as they count ‘four’ pieces. |
“Learning while having fun makes you feel like you’re not learning.” – Student
4) Good practice example
In one urban school with high numbers of Māori and Pacific students, teachers use a range of carefully selected maths games and tasks within daily, dedicated maths time. Following a strong focus on professional learning, they developed the use of predictable, purposeful routines at the start of each maths session to promote engagement, active participation, and mathematical thinking.
ERO observed a dedicated maths session in their Year 1 and 2 maths class: all students participate actively in maths tasks through three different phases. These phases are familiar to the students, who move quickly to different parts of the learning space and organise themselves in pairs, small groups, or one large group, depending on the task. This means the time for undertaking maths thinking and learning is maximised.
Each activity is briefly introduced by the teacher and offers students the opportunity to be creative and use their developing knowledge.
In the first phase, they use their developing knowledge of numbers and place value. Working in pairs, they find different ways to order the digits to create an ordered sequence between 11 and 66 on the five spaces on the rocket. Their sequence is then shared with others and checked for accuracy and differences with others.
The second phase of the maths session involves students working in pairs to show an addition equation on a number line, using pegs to demonstrate the process and solve the equation. They then move into groups of four to explain and demonstrate to one another how they got their answers.
The third phase of the session involves a worked example of a problem on a screen. Students are asked to think silently for a few minutes and then move to an area of the mat according to which answer they feel is correct – (there are four areas, one for each possible solution). They get ready to demonstrate to their peers (with equipment or using diagrams or symbols) why they have chosen that response. Students who are unsure remain in the centre and the teacher unpacks the example, demonstrating with materials to support the students to solve it. During this time, they are free to move to an area of the mat if they feel confident to choose an answer. To conclude this session, the teacher helps students to share their ideas and participate in a discussion about which response was accurate and why.
The end of the maths time closes with teachers asking the group questions, so that students can review and reflect on their learning.
5) Reflective questions for teachers
- How well do I provide my students with sufficient opportunities to learn? Do I ensure they encounter maths every day?
- How do I encourage them to be curious about maths ideas? How can I help them use maths to apply to situations and problems they encounter?
- How do I maximise the time allocated to maths so that students experience quality maths learning?
- When does the best learning happen in my maths programme?
- Who do I notice isn’t enjoying maths and how can I find out why?
This practice area is about teachers ensuring they timetable, plan for, and implement focused maths time each day. Maths sessions should be varied and engaging. This ensures that students are well-supported to learn, practise, and apply maths.
When this is going well, teachers take a deliberate approach to providing new and revisited maths learning. They encourage students to clarify their ideas, make connections, and continually build their knowledge and skills.
In this section, we set out why providing dedicated, quality maths time each day is important for students. We also offer practical guidance on how teachers can put this into practice in their own classrooms.
Overview of this section
This part of the report sets out useful information about how teachers provide dedicated maths time. It includes:
- What is this practice area?
- Why is this important?
- What does good practice look like in real life?
- Good practice example
- Reflective questions for teachers
1) What is this practice area?
“We really like to do maths, that’s why we do it every day!” - Student
This practice area is about providing daily opportunities to learn and practise maths. Daily maths should be timetabled, purposeful, and sequenced in a way that builds on existing knowledge and prepares students for further complexity. Within the time that is dedicated to maths, every effort should be made to maximise the time spent learning.
Quality daily maths involves a deliberate mix of:
- explicit instruction or opportunities to build new concepts and skills
- individual, pair, or group tasks that support students to practise new concepts and skills
- problem-based learning and more open-ended maths tasks and games that promote their interest, encourage critical thinking through wondering and questioning, and provide discussion opportunities to help teachers see how students are going and where to focus next.
Maths time should follow a clear structure, usually with a predictable motivating start followed by work time which may include group, individual, pair, or class experiences. Lessons should end with an opportunity to make connections and reflect on the learning. Sessions work best when they are designed to fully engage and include all students, helping them to build understandings and make connections to their world.
The key teaching practices discussed in this section are:
- teachers support students to learn, practise, create, and use maths daily
- teachers show students how to use maths procedures and skills accurately, efficiently, and flexibly
- teachers prompt students to talk about their maths ideas
- teachers provide cognitively challenging mathematics activities.
2) Why is this important?
Focused daily maths time is needed for students to develop their foundational maths skills and knowledge. Studies show that students achieve better in maths when they have daily exposure to maths instruction, time to practice, and opportunities for application and critical thinking.(53) At this early stage of their maths journey, it is important that young students have sufficient time to interact with and familiarise with maths concepts. This involves providing students with learning experiences at a pace that challenges them and supports their continued progress. This sets them up for positive engagement and further learning in maths: a pathway to a wide range of learning opportunities, activities, and occupations.
“Time allocated [for maths] sets the outside boundaries for what it is possible to learn. While mathematics and statistics can and should be integrated with other learning areas, setting aside focused learning time each day will provide space for increased engagement with mathematics.”
- Royal Society, 2021(54)
“Routine and structure are important to kids.” - Teacher
3) What does good practice look like in real life?
As part of this study, we talked to teachers and school leaders about the strategies that have worked well in their experience. We’ve collected their ideas and strategies here. It is important to reflect carefully about which of these will benefit each school’s unique community and context. No strategies are one-size-fits-all so all these strategies won’t be the right fit for everyone.
The key teacher practices that we focus on are:
- teachers support students to learn, practise, create, and use maths daily
- teachers show students how to use maths procedures and skills accurately, efficiently, and flexibly
- teachers prompt students to talk about their maths ideas
- teachers provide cognitively challenging maths activities.
a) Teachers support students to learn, practise, create, and use maths daily
It is more effective for students when daily maths sessions are planned out to ensure that they encounter a variety of activities. These should help students experience the breadth and depth of maths, and to learn, consolidate, and apply maths ideas. This can be done in a range of ways, but the key is to have a deliberate mix of instruction, practice, and exploration. Maths time can incorporate a selection of:
- whole-class, group, and individual tasks that revisit and practice skills and knowledge
- instructional sessions
- maths games
- problem-based learning, including complex problems
- conversations about maths
- real-world, hands-on tasks.
Problem based learning supports children’s active participation in the process of solving mathematical problems from the outset. It fosters collaborative learning, encourages knowledge retention and conceptual development, a positive attitude towards mathematics and leads to higher mathematical gains.
- O’Neill et al., 2023(55)
“Maths games are for learning and having fun at the same time.” – Student
Real-life strategies
|
We heard from teachers and school leaders that it works well to… |
|
Carefully consider the timing of maths sessions and content. Leaders and teachers in one school spoke about how they review their approach to maths across the junior school. They put strategies in place to ensure there is a consistent approach to prioritising and implementing maths. This includes a schoolwide discussion on maths topics, followed by planning sessions in the syndicate, with a strong focus on unpacking maths concepts. To strengthen their focus on maths, teachers at one school have established a consistent ‘maths time’ at the start of each day – the time that they had noticed students are most engaged. All teachers work through agreed content, and undertake assessments at the same time at the end of a unit. In their review, they had also recognised that the areas of weakest performance (e.g. fractions) were being taught later in the year. To remedy this, fractions is now taught at the start of the year, for more focus and stronger effort. |
|
Use whole-class warm-up activities. Teachers begin maths sessions through revisiting prior learning experiences by using familiar routines, practices, or equipment. These activities are an opportunity to repeat, revise, and extend on the maths ideas in focus. For example, we observed a warm-up activity called ‘Guess the number’, where students are asked to guess a number chosen by the teacher using a process of elimination with the hundreds-board as reference. Students asked questions like: “Is it bigger than 50?” “Is it an odd number?” and “Is it in the 6th row?” – to which the teacher responded, “Do you mean the 60s row, or in the 6th column?” Teachers shared that a benefit of whole-class activities is that all students in the class are exposed to ideas and concepts and can participate. Even if some are not fully confident in what they are doing, they will be exposed to ideas and concepts and be able to learn from their peers. For example, a student may only be confident counting to 20, yet a warm-up activity will include the whole class counting together to 100 using a hundreds-board. |
|
Use a ‘number of the day’ to frame discussions of maths concepts. Many of the schools we talked to use this strategy. For example, in one class the number 42 is introduced as the ‘number of the day’ in the warm-up activity. The teacher asks students: · What is it? (e.g., number 42) · What numbers come before/after? · What number is less/more? · How do you spell it? · What is 42 + [random numbers] · Partition 42 using place value · Round 42 to the nearest 10 · Arrange the random numbers (including 42) in ascending order. |
|
Choose active or hands-on activities for practising new learning. In one Year 1 class, students are given a number from 0-10 and line up in the correct order to make a human number-line.
|
|
Offer a range of difficulty options. In one classroom we visited, the teacher offers students a choice of activities which range in difficulty from ‘mild’ (easy), to ‘medium’, to ‘hot’ (more difficult). Students choose the level of challenge. The teacher shared that she monitors the difficulty levels being selected as part of her informal formative assessment of students’ confidence, and notes what areas of learning need extra attention. The teacher has noted that this activity supports confidence and motivation in the class: being able to complete an activity independently, no matter the difficulty level, encourages students to feel confident and successful. |
b) Teachers show students how to use maths procedures and skills accurately, efficiently, and flexibly
Teachers need to provide multiple opportunities for students to build up their toolkit of strategies (flexible ways to solve a problem) and procedures for solving maths problems. These need to be based on good understandings of the strategies, rather than following rigid, step-by-step processes or learning a set of rules.
“When students use a procedure they do not understand, they are more likely to make errors and fail to notice when the answer does not make sense.”
- National Council of Teachers of Mathematics, 2023(56)
In practice, this means that teachers need to provide opportunities for students to learn new strategies and procedures, practise using them so that they become proficient, and apply them confidently in a range of contexts. This includes supporting students to make connections between strategies.
Understanding is much more valuable than memorisation
When teachers focus on helping students memorise maths facts or procedures without understanding them, they are not supporting students in the long term. Memorising a rigid set of rules or reciting rote-learning alone without other methods of teaching those concepts may help students get answers correct in Years 1-3, but won’t provide the solid grounding of understanding that is needed for the next parts of those students’ maths journeys.
For example, basic facts can be taught using number relationships and reasoning strategies, not memorisation. A 10s frame which shows 7 counters helps students to see what 7 looks like (and how it mirrors how they show 7 with their hands). It also illustrates basic facts such as 5+2=7, 7-5=2 as well as 10-7=3, 7+3=10 . This understanding helps students to start building strategies beyond basic facts too – such as ‘making a whole’ with fractions and decimals – 7/10, .7 etc.
Real-life strategies
|
We heard from teachers and school leaders that it works well to… |
|
Provide repeated opportunities to encounter and practise ideas through a range of contexts, activities, and equipment. For example, the teacher uses both the hundreds-board and number blocks to teach the students to count in 10s. The teacher incorporates repetition into a warm-up activity to practise prior learning (e.g., counting together on the hundreds-board, counting in 5s on the abacus), or part of scaffolding a new skill (e.g., learning the 4x tables). Repetition of counting sequences, patterns, and basic knowledge helps students to memorise and recognise them. |
|
Set tasks that deliberately link to students’ experiences or interests. For example, the teacher introduces a problem where students imagine they are at a birthday party, and need to partition the birthday cake into 8 equal pieces. The students must figure out the best strategy to do this. This problem gets students thinking about different maths procedures, including division (dividing a whole to make 8) and multiplication (multiply the number of pieces to make 8). During the lesson, the teacher actively reminds students of how these link to strategies or knowledge recently covered. |
|
Use carefully selected maths games for introducing and practising maths ideas. We observed classes where the use of maths games is an important part of maths time. In one class, tables are set out with selected games, aligned to the teaching focus. The purpose of the games is clearly identified on a card with the instructions and students make a record of what they are doing. Teachers we spoke with promote maths games that are sometimes physical (e.g., a board game or something that uses materials) or digital (e.g., on an iPad). Games are played in whole-class or group settings, often independent of the teacher. Teachers shared that they purposefully select specific games to link to current or recent maths learning. They also consider whether the games can generate sharing and discussion of ideas among students, and whether they will offer sufficient challenge while still being accessible. |
“When we go on the mat for learning, I like doing graphs and tally marks. I love how they add up together.” - Student
c)Teachers prompt students to talk about their maths ideas
Engaging in ‘maths’ talk helps students to think critically and make sense of their own and others’ ideas. It also supports teachers to monitor students’ accuracy and complexity of maths thinking. That way, they can quickly respond to any misunderstandings that need to be corrected.
In practice, teachers have a key role in questioning students as well as creating a classroom which is full of maths discussion. This can be done by creating regular opportunities for conversations about mathematical ideas with individuals or small groups. Teachers might encourage students to ask questions, explain why they have come to a particular answer, or why they agree or disagree with others’ ideas. Mutual respect and high expectations from the teacher are crucial for students to feel confident in contributing their thoughts and engaging with their peers’ ideas.
Real-life strategies
|
We heard from teachers and school leaders that it works well to… |
|
Focus on developing students’ use of mathematical language and vocabulary. This equips students for discussions about their maths thinking. For example, one teacher introduces specific maths vocabulary during maths time and encourages students to use these words when explaining their answers to maths problems. The teacher also uses warm-up activities like counting together to reinforce ideas, such as the difference between ‘ty’ (i.e., thirty) and ‘teen’ (i.e., thirteen). When counting together using a hundreds-board for example, students are encouraged to loudly emphasise these sounds as a way of committing them to memory. |
|
Encourage students to describe their thinking. This helps students to explain their thinking and how they solved a problem. For example, a teacher prompts students with questions like, “Why do you think that?” and “Can you explain to your classmates how you got that answer?” This encourages students to explain their thinking in their own words and practice using the maths language that they have been learning (e.g., words like “probably” and “because”). The intent of this strategy is to get the student to think about the approach they used to solve a problem, and to share this with other students. |
|
Use questioning and prompts to guide students as they attempt to solve a maths problem. The teacher guides students to use a particular approach, asking, “What would happen if you tried…” If an answer is incorrect, the teacher asks questions to prompt them to reassess their answer and their approach, using phrases like, “Why do you think that?” or “Tell me about how you came up with this answer.” |
|
Explicitly teach maths words, and talk about the connections between them. As part of a lesson in statistics, one teacher asks her mixed class of Year 1s and 2s if anyone can explain the meaning of the word ‘probability’. Some students respond using words they had learnt previously: ‘possibly’ and ‘probably’. The teacher had taught these students to use accompanying hand gestures:
The class’s understanding of these similar mathematical words paves the way for their understanding of the new term ‘probability’. |
|
Use what one student says to prompt wider discussion. For example, a teacher presents a maths problem and asks a student to explain how they reached their answer. This is sometimes referred to as ‘justifying’ their answer. The student’s answer is used to prompt reactions from other students – “Do you agree or disagree? Why?” |
d) Teachers provide cognitively challenging maths activities
Students benefit from maths tasks that make them engage in maths thinking where the answer is not obvious. This is often done through presenting maths problems to solve (either real-life or imagined) which take time and may require support from equipment, visual representations, and prompts from the teacher. These sorts of tasks, sometimes called ‘challenging tasks’, or ‘rich tasks’,(57) offer all students the opportunity to participate and be stretched.
“All students [should be] working on ‘worthwhile, challenging tasks conducive to productive struggle’ (effortful learning requiring reasoning, problem solving, and perseverance).” - Ministry of Education, 2022(58)
“Children’s mana and self-esteem is uplifted when they can solve problems themselves.” - Teacher
Real-life strategies
|
We heard from teachers and school leaders that it works well to… |
|
Use photographs as prompts for complex peer discussions. In one class, students are asked to predict from a series of photographs: “How many glass beads in the jar?” and “How many now?” when the number of beads increase. Students share what they think with their partner and share back with the larger group. The teacher responds by drawing out their thinking, illustrating with diagrams or equations, and building on what they offer.
|
|
Ask questions with lots of possible answers or approaches. For example, in the context of measurement, looking at area and perimeter concepts: “Draw some letters of the alphabet on squared paper using exactly 10 squares” or “Using equipment or symbols, show five different ways of showing the number 15.” This task has endless solutions, and can support students who are just beginning to understand how many 15 is, what it looks like with different kinds of equipment and representation, or where it falls in a counting sequence, as well as those who are able to represent 15 as 3 times 5, or a quarter of 60, or 340 – 325, 10 times bigger than 1.5, etc. In a Year 1-2 class, a group of mixed-ability students are required to split a cake represented by a piece of paper into four parts. Confident students fold the paper over twice to ensure all parts are equal, and less confident students manually draw lines across the paper as they count ‘four’ pieces. |
“Learning while having fun makes you feel like you’re not learning.” – Student
4) Good practice example
In one urban school with high numbers of Māori and Pacific students, teachers use a range of carefully selected maths games and tasks within daily, dedicated maths time. Following a strong focus on professional learning, they developed the use of predictable, purposeful routines at the start of each maths session to promote engagement, active participation, and mathematical thinking.
ERO observed a dedicated maths session in their Year 1 and 2 maths class: all students participate actively in maths tasks through three different phases. These phases are familiar to the students, who move quickly to different parts of the learning space and organise themselves in pairs, small groups, or one large group, depending on the task. This means the time for undertaking maths thinking and learning is maximised.
Each activity is briefly introduced by the teacher and offers students the opportunity to be creative and use their developing knowledge.
In the first phase, they use their developing knowledge of numbers and place value. Working in pairs, they find different ways to order the digits to create an ordered sequence between 11 and 66 on the five spaces on the rocket. Their sequence is then shared with others and checked for accuracy and differences with others.
The second phase of the maths session involves students working in pairs to show an addition equation on a number line, using pegs to demonstrate the process and solve the equation. They then move into groups of four to explain and demonstrate to one another how they got their answers.
The third phase of the session involves a worked example of a problem on a screen. Students are asked to think silently for a few minutes and then move to an area of the mat according to which answer they feel is correct – (there are four areas, one for each possible solution). They get ready to demonstrate to their peers (with equipment or using diagrams or symbols) why they have chosen that response. Students who are unsure remain in the centre and the teacher unpacks the example, demonstrating with materials to support the students to solve it. During this time, they are free to move to an area of the mat if they feel confident to choose an answer. To conclude this session, the teacher helps students to share their ideas and participate in a discussion about which response was accurate and why.
The end of the maths time closes with teachers asking the group questions, so that students can review and reflect on their learning.
5) Reflective questions for teachers
- How well do I provide my students with sufficient opportunities to learn? Do I ensure they encounter maths every day?
- How do I encourage them to be curious about maths ideas? How can I help them use maths to apply to situations and problems they encounter?
- How do I maximise the time allocated to maths so that students experience quality maths learning?
- When does the best learning happen in my maths programme?
- Who do I notice isn’t enjoying maths and how can I find out why?
Practice area 4: Teachers notice when students require extra support for learning and provide effective targeted teaching
This practice area is about paying attention to students who may demonstrate a lack of engagement, motivation, or success in maths. Teachers recognise when to support or extend a student, when to move on to new learning, or when to spend longer on an area to consolidate learning for individual students.
When this is going well, maths learning is accessible and sufficiently challenging for all students. Teachers are clear about students’ specific maths strengths and needs and have clear, targeted plans for support where needed. Approaches are collaboratively planned and effectively address any areas requiring attention, motivate students to fully engage in maths, and build their confidence and competence.
In this section we outline considerations for identifying and supporting these students. We highlight why it is important to identify and monitor their engagement and progress, and the importance of careful planning and involving others. We also offer practical guidance on how teachers can put this into practice in their own classrooms.
Overview of this section
This part of the report sets out useful information about how teachers can recognise and target teaching for students who require additional support. It includes:
- What is this practice area?
- Why is this important?
- What does good practice look like in real life?
- Good practice example
- Reflective questions for teachers
1) What is this practice area?
This practice area is about teachers targeting their teaching for individual students. Students may sometimes demonstrate a lack of engagement, motivation, or success in maths. Teachers need to understand any barriers to learning and find effective ways to work with students and their families to ensure they progress. This includes considering whether students have sufficiently mastered learning in an area, or are sufficiently challenged in their learning, when teachers are making decisions about whether to move on. A focused effort is needed to ensure all students in the class have access to challenge and success in maths. At times, this might require additional expertise or resourcing.
The key teaching practices discussed in this section are:
- teachers identify and monitor students who need additional support
- teachers partner with others and are supported to implement targeted approaches
- teachers support students with identified needs to access and engage through planned and targeted interventions
- teachers extend competent maths students through adding challenge and complexity.
2) Why is this important?
“When students ‘fail to thrive’ [at maths] they often lose confidence in their ability, lose confidence in the school environment as a place to which they belong, develop poor attitudes to learning and to school, and disengage from learning opportunities.”
- Gervarsoni & Lindenskov, 2011(60)
Foundational maths concepts and attitudes that are learnt during the first few years of school set students up for success – or struggle – for the rest of their maths journey throughout schooling and into adulthood. Early experiences of maths leave lasting impressions and impact on students’ ongoing interest and engagement in maths. It is essential teachers are alert to early signs of difficulty or lack of motivation and act on these promptly.
An important consideration for teachers when working with students who are feeling overly or insufficiently challenged in maths, is students’ self-beliefs and attitudes about maths.(61) Students of any current ability level with positive self-beliefs, are confident that they are capable of learning and improving at maths, and motivated to do so.
All students should have opportunities to experience challenge and success on their journey to mastering a current maths focus. Students may not be engaged or making progress in maths for a range of reasons.(62) It can be tempting to hope that students will catch up or re-engage on their own, or that things will click into place later on in their maths journey. However, students not finding success early with maths learning are at risk of missing important knowledge or understanding to build on as they move through school. Students who find success easily are also at risk, as they can lack motivation to tackle more complex maths, particularly if they have minimal experience of mathematical ”productive struggle” throughout their time in school. They should know that being stuck is normal and an important part of mathematical problem solving.(63)
“Teachers and learners should also have high expectations and ensure that learners are moving towards explicit success criteria using the goldilocks principles of challenge. The goldilocks principles of challenge ensure that teachers are focusing on work that is not too easy, but also not too hard, so as to avoid cognitive overload. By providing material that is deemed right for learners, a focus on learning is created with the right proportion of surface to deep learning taking place.”
- Hattie, 2021(64)
3) What does good practice look like in real life?
As part of this study, we talked to teachers and school leaders about the strategies that have worked well in their experience. We’ve collected their ideas and strategies here. It is important to reflect carefully about which of these will benefit each school’s unique community and context. No strategies are one-size-fits-all so all these strategies won’t be the right fit for everyone.
The key teacher practices that we focus on are:
- teachers identify and monitor students who need additional support
- teachers partner with others to implement targeted approaches
- teachers support students with identified needs to access and engage through planned and structured programmes
- teachers extend competent maths students through adding challenge and complexity.
a) Teachers identify and monitor students who need additional support
Teachers need to begin by assessing any foundational knowledge that might not be fully mastered and consider what factors might be contributing to a lack of engagement or success. This may involve looking for patterns across other learning areas, talking with parents/whānau and other teachers, and looking at a range of information about the student to determine how to proceed.
Real-life strategies
|
We heard from teachers and school leaders that it works well to… |
|
Use diagnostic assessments to identify areas of strength or areas requiring improvement. Teachers we spoke to often use assessments as a way of diagnosing areas of difficulty, or missing pieces in students’ understanding or knowledge. For example, teachers use initial maths assessments (e.g., JAM) to see if there are areas which may require specific focus. |
|
Identify students for support through in-the-moment teaching interactions. Teachers we spoke to are alert to how students engage as they work with larger groups. They use questioning to dig into their understanding and to identify students who require additional support. |
|
Monitor engagement and success through records of learning and regular checks. Teachers develop plans which monitor progress towards specific goals, which are checked on regularly. These are sometimes monitored by the student themselves or by support staff as well as parents/whānau. Learning portfolios and modelling books are sometimes used to show evidence of progress. |
“[It is] really important that kids actually experience success.” – Teacher
b) Teachers partner with others and are supported to implement targeted approaches
The teacher works alongside students to help them identify their goals, decides on a course of action and monitors their progress. Partnering with their families/ whānau and specialist support staff is also essential to ensure that introduced approaches or interventions have the maximum chance of success.
Teachers who aren’t sure where to seek guidance from, can prioritise seeking support for their immediate teaching and next steps. Teachers can talk to, for example:
- syndicate, curriculum, or senior leaders
- Resource Teachers: Learning and Behaviour (RTLB) staff, specialist support staff, teacher aides who have specialise expertise/ training
- experienced colleagues
- maths specialist teachers
- maths experts within the wider community, e.g., Kahui Ako, regional school clusters
- professional learning providers who specialise in maths.
Real-life strategies
|
We heard from teachers and school leaders that it works well to… |
|
Agree on goals for learning. Teachers hold discussions with a student and their parents/whānau to settle on areas for focus. This helps everyone to be clear about what support is being provided and why. This begins with discussions about identified needs and the assessments used to support this. |
|
Develop collaborative and individualised learning plans. Some schools provide this through an Individual Learning Plan process. These plans include details of interventions or programmes to be used, how whānau can be involved, and how progress will be shared. An important aspect of this is ensuring the student is involved. |
|
Support students to stay motivated. Teachers we spoke to focus on ways to make learning interesting, accessible, and challenging for their students. They do this through the tasks they select, for example choosing ‘authentic’ and complex problems which are connected to the student’s world. Teachers regularly check in with students to show interest in their strategies and progress. Motivation is also supported by opportunities to share and celebrate their learning. Introducing an element of competition can also be motivating for students – “Who can find the most (or most interesting) solutions?” |
|
Involve experts and specialist staff. Schools we visited talked about how they talk to the students and their family/whānau to develop an individualised plan to support improvement in maths. Teachers, leaders, students, and whānau (and specialists if relevant) develop a clear goal and actions to be taken. In one school ERO visited, leaders and teachers outlined their top priorities for responding to individual students in maths: o teachers know the students and oversee all students’ learning programmes (including those who need extra support) o teachers plan maths tasks based on how their students work best o all students have opportunities to participate in mixed ability grouping o students are matched carefully with buddies or familiar small groups, based on needs and strengths. |
Mindsets and attitudes to learning
It is well-established that students’ attitudes and beliefs about themselves as students have a strong motivating – or demotivating – effect. Teachers can support students to develop a positive attitude about their maths learning capabilities, through purposeful choice of tasks and language.
Students who are struggling and students who need more challenge are at risk of disengagement, so their attitudes to maths learning are particularly important. Having a ‘growth’ or ‘fixed’ mindset (65) significantly impacts on how students engage in maths, but there are actions teachers can take to help:
“Students with a growth mindset:
- believe they can get smarter by trying hard
- tend to have a resilient response to failure; remain focused on mastering skills and knowledge even when challenged
- do not see failure as an indictment on themselves
- believe that effort leads to success.
Students with a fixed mindset:
- believe they are as smart as they will ever get
- seek success but mainly on tasks with which they are familiar
- avoid or give up quickly on challenging tasks
- derive their perception of ability from their capacity to attract recognition
Teachers can change mindsets through:
- the things they affirm (effort, persistence, cooperation, learning from others, flexible thinking)
- the way they affirm – ‘You did not give up even though you were stuck! You tried something different! You tried to find more than one answer!’
- the types of tasks they pose.” Sullivan et al., 2011(66)
c) Teachers support students with identified needs to access and engage through planned and targeted interventions
Structured interventions and programmes can be effective. A large-scale analysis of the global evidence around maths teaching for ages 3-7 found that many children who may need
additional support with early maths can return to a typical learning trajectory, with varied teaching methods and targeted attention. This means that after a period of intervention and support, most struggling students soon return to the learning level of their peers. Research shows that when these intervention periods are of good quality, they can be effective for students who need extra support, particularly when they are evidence-based and applied in a structured, deliberate way. (67) See below for key features of good quality targeted support interventions.
Key features of good quality structured mathematics interventions
The Education Endowment Foundation looked at the benefits of targeted maths interventions, for students aged 3-7. Their report outlines the key features that make good interventions work well.
“Consider the following to make the most of targeted support:
- use more experienced staff to support children with the greatest needs
- provide training and support for staff using targeted activities, including structured resources or activity plans with clear objectives
- sessions should be brief and regular
- quality is generally more important than quantity— there is some evidence to suggest that time-limited interventions may be more effective
- make explicit connections between targeted support and everyday activities or teaching; practitioners delivering additional support should have time to discuss this work with their colleagues.”
- Clark, Henderson, & Gifford, 2020(68)
Real-life strategies
|
We heard from teachers and school leaders that it works well to… |
|
Provide short-term interventions with a specific focus. One school ERO visited emphasised that it is the responsibility of classroom teachers to identify students that need extra help. When teachers become concerned about progress, the school moves quickly to put a structured programme in place. A common intervention at this school is for teacher aides who are trained in a targeted maths intervention to run a 15-minute structured intervention programme during the class maths lesson. These sessions are linked back to the content of the main session. The students in the intervention group join their peers for the majority of maths time. |
|
Offer students additional optional workshops in class as a follow-up. We observed teachers who introduce a task or maths concept to a larger group, and then check with students about their level of confidence. They then offer opportunities for students to stay back, join an additional workshop, or have one-to-one teacher support if they choose to. The follow-up activity sometimes involves working more deliberately through the original task with added materials, explanations, and diagrams. Teachers provide additional opportunities for students to talk about and show their ideas as they tackle similar tasks. |
|
Provide additional maths sessions. Schools sometimes supplement their current programme with additional sessions for students who are struggling. These sessions use familiar games and activities to practise using their skills and building their knowledge. For example, playing a board game to focus students on accurately counting forward or backward, or to practise basic facts to ten. These sessions focus strongly on consolidating learning, the accurate use of maths vocabulary, and sometimes introducing ideas that they are about to encounter in their classroom maths. |
|
Support from teacher aides |
|
ERO research shows that - unless the teacher aide has appropriate specialist qualifications to do so - it is not good practice for teacher aides to be the main people that plan for students that need extra support. The evidence is clear that this contributes to poorer outcomes for those students. Instead, it should be qualified teachers that adapt and oversee the learning of those students. A great alternative to traditional ‘velcro’ teacher aide support is for teacher aides to work across the wider class, rotating support for all students on their maths tasks based on discussions with the classroom teacher. This enables teachers to work more regularly with those students that need extra support in maths, which has proven benefits for these students. As a general rule of thumb, teachers should spend at least as much time supporting students that need targeted support as they do with the rest of the class. While teacher aides should not have overall responsibility for students’ programmes, tasks, or assessments, they can have a supportive role in the delivery of structured maths interventions. However, this only works when teacher aides deliver interventions as instructed, based on robust training, with a highly structured approach. Research shows that when teacher aides don’t use the intended structure – for example, not using resources, or condensing several short sessions into one long one – this has a negative impact on student learning. Teachers can help teacher aides do their best work through lots of communication, robust training, and careful timetabling, so that structured intervention sessions link to classroom maths learning. These sessions might occur within the classroom, for example, while all students are working in small groups. Teachers can also support teacher aides to develop and fine-tune their intervention delivery practices through professional discussions, observations, and modelling. Discussions should include clarifying why a maths intervention was chosen for a particular student – talking about the evidence base, or the assessments that led to this decision. This helps teacher aides to buy in to the ‘how and why’ of the intervention. For more about teachers and teacher aides working together, see A practical guide for teachers: What quality teacher aide practice looks like (ero.govt.nz)(69) |
Programme example: Accelerated Learning in Mathematics (ALiM)
Accelerating Learning in Mathematics (ALiM) is a Ministry of Education initiative used commonly in Aotearoa New Zealand schools. The programme is designed to lift achievement in maths for students in Years 1-10 who have fallen behind the achievement level of their peers. ALiM is designed as a short-term intervention to be used in addition to a school’s regular maths programme. Teachers complete “cycles of inquiry” focused on accelerating the achievement levels of target students, increasing the rate of their learning to reach the level of their peers.(70) Schools decide the timing and length of these cycles for themselves. An ALiM session might see teachers introduce activities that, for the majority of students in the class, can be done with minimum teacher intervention. When this is working well, most students are undertake targeted maths tasks that are both engaging and meaningful, and the teacher is freed up to help students that require extra support.(71) A key feature of the ALiM programme is partnering with families/whānau to support maths learning.(72)
d) Teachers support competent maths students through adding challenge and complexity
Research shows that highly capable students are at risk of disengagement from learning - similar to their peers who need support to build foundational learning skills and knowledge. Students who demonstrate a very strong capability in maths require attentive and targeted support, so that they have equitable opportunities to make progress at school just like their peers are able to.
“Without appropriate challenge, gifted students are ‘at risk’; they may demonstrate boredom, loss of interest in or commitment to mathematics, limited metacognition, and poor behaviour.”
- Diezmann & Watters, 1997(73)
Teachers need to be well-equipped and confident with a range of extra-challenge strategies to support these students engaging in maths learning alongside (rather than in isolation from) their peers. Strategies may involve enriching, extending, or accelerating their learning through complex and challenging tasks, or providing additional experiences or materials and representations. Some teachers will need support to build these practices, and will benefit from working with curriculum leaders or seeking external support.
Real-life strategies
|
We heard from teachers and school leaders that it works well to… |
|
Use assessments to be clear and specific about learning levels. Assessments should be used to identify the need for targeted action. Teachers use a combination of formal (using tools) and informal assessment. This helps teachers to be clear and specific about students’ level of understanding, and where targeted challenge is needed. For example, we saw teachers observe students’ levels of engagement and interest during maths sessions, whether they complete tasks very quickly or at a superficial level, and whether they exhibit off-task behaviours. |
|
Add challenge and complexity to classroom tasks (‘problematisation’ of tasks). Teachers find ways to modify or add challenge to class tasks for their able students. For example: When doing a warm-up activity counting from 19, a teacher provides additional challenge by asking students to count from 119, or 3019. (See the box below for more about problematisation.) |
|
Providing ‘challenging tasks’ and investigations. Providing ‘challenging tasks’ (see the box below) is an effective strategy for supporting students to engage more fully in maths sessions along with their peers, while expanding their knowledge and understanding. For example, a class investigation involving measurement and statistics allows students who are competent in measurement and graphing concepts to show leadership, and to apply and extend their knowledge and skills. They support their peers to investigate how the length of shadows change throughout the day. They collaborate in groups of three to measure their shadows in the playground. They record this information in their books, and then decide how best to present the information for others to understand. Note: Mathematical investigations are where students use their maths understanding in various situations. Investigations often begin with a 'real world' mathematical question and allow for a range of approaches or solutions. |
Tips for engaging students who require additional challenge
There are some key things teachers can do to help students who require additional challenge to engage more fully in maths.
These include:
- minimising time spent memorising facts or practising skills that are already mastered
- delaying direct teacher support so that students have sufficient opportunity to work with maths problems, encounter the complexities in tasks, and test and talk through their own approaches with peers
- asking students to record explanations and reflect on their thinking
- encouraging students to work with peers to share their ideas and learn from others
- ensuring each whole-class activity offers opportunities for competent students to draw on a wide range of knowledge and find additional solutions
- inviting students to communicate their solutions and offering feedback to refine their strategies and ideas
- ensuring they aren’t just ‘left to it’ during maths time. Teachers should allow space, but remember to check in with students. This might involve timely suggestions, prompting questions, engaging in debate, reminders of relevant learning or knowledge, or provision of carefully considered resources, materials, and representations.
What are challenging tasks?
Challenging tasks (also called “rich tasks‟) are complex maths problems that don’t have a single or obvious answer. Students are not initially aware of how to solve the task and have to invent mathematical actions to solve it.
These sorts of tasks enhance motivation and help students to develop confidence, capability, and curiosity (“mathematical power”(74)) through high-level thinking and reasoning. Such tasks also encourage metacognitive skills, helping students understand and develop control over how they are thinking.(75)
Challenging tasks are complex and absorbing mathematical problems that:
- require students to process multiple pieces of mathematical information at the same time and make connections between them
- have more than one possible solution or solution method
- involve more than one mathematical step
- are perceived as both engaging and challenging by students.
What is problematisation?
Problematisation is when an existing maths task is adjusted by the teacher to be more complex or challenging. Methods for problematisation can include “inserting obstacles to the solutions, removing some information, or requiring students to use particular representations or develop generalisations.”(76) Younger students in particular benefit from adjusted maths games and more access to manipulative tools and equipment.
“The construction of a number line to represent the distance of the ten brightest stars. This required the application of knowledge of large numbers, relative magnitude, and scale—and extension of the more typical use of the number line to represent sets of numbers.”
- Diezmann & English, 2001a
2) Good practice example
One school ensures they provide additional support or targeted teaching for all their students within the classroom by including teacher aides as part of their daily programme. The teacher aides participate in maths professional learning sessions alongside teachers and are fully informed about the maths ideas included in each lesson. This includes understanding the maths embedded in the games, and how to highlight and support students to access these.
The teacher aides are active in the lessons, working alongside teachers to offer support to identified students in the context of the various parts of the programme. Sometimes this includes helping them to use materials to solve a problem, or supporting them as they work alongside a partner or participate in a larger group. Teachers help the student to use the knowledge they have, understand and use maths vocabulary, or learn how to play a game which supports their skill development.
5) Reflective questions for teachers
- Am I noticing disengagement, or lack of confidence or progress in any of my students?
- Do I know if this is because the student finds the maths learning too easy or too hard?
- If too hard – are there alternative approaches, materials, or representations I could try? Are there some negative learning experiences influencing their engagement, or learning needs or disabilities to take account of?
- If too easy – do students have enough opportunities to grapple with authentic, complex, or challenging tasks?
- Have I spoken to this student about what they think?
This practice area is about paying attention to students who may demonstrate a lack of engagement, motivation, or success in maths. Teachers recognise when to support or extend a student, when to move on to new learning, or when to spend longer on an area to consolidate learning for individual students.
When this is going well, maths learning is accessible and sufficiently challenging for all students. Teachers are clear about students’ specific maths strengths and needs and have clear, targeted plans for support where needed. Approaches are collaboratively planned and effectively address any areas requiring attention, motivate students to fully engage in maths, and build their confidence and competence.
In this section we outline considerations for identifying and supporting these students. We highlight why it is important to identify and monitor their engagement and progress, and the importance of careful planning and involving others. We also offer practical guidance on how teachers can put this into practice in their own classrooms.
Overview of this section
This part of the report sets out useful information about how teachers can recognise and target teaching for students who require additional support. It includes:
- What is this practice area?
- Why is this important?
- What does good practice look like in real life?
- Good practice example
- Reflective questions for teachers
1) What is this practice area?
This practice area is about teachers targeting their teaching for individual students. Students may sometimes demonstrate a lack of engagement, motivation, or success in maths. Teachers need to understand any barriers to learning and find effective ways to work with students and their families to ensure they progress. This includes considering whether students have sufficiently mastered learning in an area, or are sufficiently challenged in their learning, when teachers are making decisions about whether to move on. A focused effort is needed to ensure all students in the class have access to challenge and success in maths. At times, this might require additional expertise or resourcing.
The key teaching practices discussed in this section are:
- teachers identify and monitor students who need additional support
- teachers partner with others and are supported to implement targeted approaches
- teachers support students with identified needs to access and engage through planned and targeted interventions
- teachers extend competent maths students through adding challenge and complexity.
2) Why is this important?
“When students ‘fail to thrive’ [at maths] they often lose confidence in their ability, lose confidence in the school environment as a place to which they belong, develop poor attitudes to learning and to school, and disengage from learning opportunities.”
- Gervarsoni & Lindenskov, 2011(60)
Foundational maths concepts and attitudes that are learnt during the first few years of school set students up for success – or struggle – for the rest of their maths journey throughout schooling and into adulthood. Early experiences of maths leave lasting impressions and impact on students’ ongoing interest and engagement in maths. It is essential teachers are alert to early signs of difficulty or lack of motivation and act on these promptly.
An important consideration for teachers when working with students who are feeling overly or insufficiently challenged in maths, is students’ self-beliefs and attitudes about maths.(61) Students of any current ability level with positive self-beliefs, are confident that they are capable of learning and improving at maths, and motivated to do so.
All students should have opportunities to experience challenge and success on their journey to mastering a current maths focus. Students may not be engaged or making progress in maths for a range of reasons.(62) It can be tempting to hope that students will catch up or re-engage on their own, or that things will click into place later on in their maths journey. However, students not finding success early with maths learning are at risk of missing important knowledge or understanding to build on as they move through school. Students who find success easily are also at risk, as they can lack motivation to tackle more complex maths, particularly if they have minimal experience of mathematical ”productive struggle” throughout their time in school. They should know that being stuck is normal and an important part of mathematical problem solving.(63)
“Teachers and learners should also have high expectations and ensure that learners are moving towards explicit success criteria using the goldilocks principles of challenge. The goldilocks principles of challenge ensure that teachers are focusing on work that is not too easy, but also not too hard, so as to avoid cognitive overload. By providing material that is deemed right for learners, a focus on learning is created with the right proportion of surface to deep learning taking place.”
- Hattie, 2021(64)
3) What does good practice look like in real life?
As part of this study, we talked to teachers and school leaders about the strategies that have worked well in their experience. We’ve collected their ideas and strategies here. It is important to reflect carefully about which of these will benefit each school’s unique community and context. No strategies are one-size-fits-all so all these strategies won’t be the right fit for everyone.
The key teacher practices that we focus on are:
- teachers identify and monitor students who need additional support
- teachers partner with others to implement targeted approaches
- teachers support students with identified needs to access and engage through planned and structured programmes
- teachers extend competent maths students through adding challenge and complexity.
a) Teachers identify and monitor students who need additional support
Teachers need to begin by assessing any foundational knowledge that might not be fully mastered and consider what factors might be contributing to a lack of engagement or success. This may involve looking for patterns across other learning areas, talking with parents/whānau and other teachers, and looking at a range of information about the student to determine how to proceed.
Real-life strategies
|
We heard from teachers and school leaders that it works well to… |
|
Use diagnostic assessments to identify areas of strength or areas requiring improvement. Teachers we spoke to often use assessments as a way of diagnosing areas of difficulty, or missing pieces in students’ understanding or knowledge. For example, teachers use initial maths assessments (e.g., JAM) to see if there are areas which may require specific focus. |
|
Identify students for support through in-the-moment teaching interactions. Teachers we spoke to are alert to how students engage as they work with larger groups. They use questioning to dig into their understanding and to identify students who require additional support. |
|
Monitor engagement and success through records of learning and regular checks. Teachers develop plans which monitor progress towards specific goals, which are checked on regularly. These are sometimes monitored by the student themselves or by support staff as well as parents/whānau. Learning portfolios and modelling books are sometimes used to show evidence of progress. |
“[It is] really important that kids actually experience success.” – Teacher
b) Teachers partner with others and are supported to implement targeted approaches
The teacher works alongside students to help them identify their goals, decides on a course of action and monitors their progress. Partnering with their families/ whānau and specialist support staff is also essential to ensure that introduced approaches or interventions have the maximum chance of success.
Teachers who aren’t sure where to seek guidance from, can prioritise seeking support for their immediate teaching and next steps. Teachers can talk to, for example:
- syndicate, curriculum, or senior leaders
- Resource Teachers: Learning and Behaviour (RTLB) staff, specialist support staff, teacher aides who have specialise expertise/ training
- experienced colleagues
- maths specialist teachers
- maths experts within the wider community, e.g., Kahui Ako, regional school clusters
- professional learning providers who specialise in maths.
Real-life strategies
|
We heard from teachers and school leaders that it works well to… |
|
Agree on goals for learning. Teachers hold discussions with a student and their parents/whānau to settle on areas for focus. This helps everyone to be clear about what support is being provided and why. This begins with discussions about identified needs and the assessments used to support this. |
|
Develop collaborative and individualised learning plans. Some schools provide this through an Individual Learning Plan process. These plans include details of interventions or programmes to be used, how whānau can be involved, and how progress will be shared. An important aspect of this is ensuring the student is involved. |
|
Support students to stay motivated. Teachers we spoke to focus on ways to make learning interesting, accessible, and challenging for their students. They do this through the tasks they select, for example choosing ‘authentic’ and complex problems which are connected to the student’s world. Teachers regularly check in with students to show interest in their strategies and progress. Motivation is also supported by opportunities to share and celebrate their learning. Introducing an element of competition can also be motivating for students – “Who can find the most (or most interesting) solutions?” |
|
Involve experts and specialist staff. Schools we visited talked about how they talk to the students and their family/whānau to develop an individualised plan to support improvement in maths. Teachers, leaders, students, and whānau (and specialists if relevant) develop a clear goal and actions to be taken. In one school ERO visited, leaders and teachers outlined their top priorities for responding to individual students in maths: o teachers know the students and oversee all students’ learning programmes (including those who need extra support) o teachers plan maths tasks based on how their students work best o all students have opportunities to participate in mixed ability grouping o students are matched carefully with buddies or familiar small groups, based on needs and strengths. |
Mindsets and attitudes to learning
It is well-established that students’ attitudes and beliefs about themselves as students have a strong motivating – or demotivating – effect. Teachers can support students to develop a positive attitude about their maths learning capabilities, through purposeful choice of tasks and language.
Students who are struggling and students who need more challenge are at risk of disengagement, so their attitudes to maths learning are particularly important. Having a ‘growth’ or ‘fixed’ mindset (65) significantly impacts on how students engage in maths, but there are actions teachers can take to help:
“Students with a growth mindset:
- believe they can get smarter by trying hard
- tend to have a resilient response to failure; remain focused on mastering skills and knowledge even when challenged
- do not see failure as an indictment on themselves
- believe that effort leads to success.
Students with a fixed mindset:
- believe they are as smart as they will ever get
- seek success but mainly on tasks with which they are familiar
- avoid or give up quickly on challenging tasks
- derive their perception of ability from their capacity to attract recognition
Teachers can change mindsets through:
- the things they affirm (effort, persistence, cooperation, learning from others, flexible thinking)
- the way they affirm – ‘You did not give up even though you were stuck! You tried something different! You tried to find more than one answer!’
- the types of tasks they pose.” Sullivan et al., 2011(66)
c) Teachers support students with identified needs to access and engage through planned and targeted interventions
Structured interventions and programmes can be effective. A large-scale analysis of the global evidence around maths teaching for ages 3-7 found that many children who may need
additional support with early maths can return to a typical learning trajectory, with varied teaching methods and targeted attention. This means that after a period of intervention and support, most struggling students soon return to the learning level of their peers. Research shows that when these intervention periods are of good quality, they can be effective for students who need extra support, particularly when they are evidence-based and applied in a structured, deliberate way. (67) See below for key features of good quality targeted support interventions.
Key features of good quality structured mathematics interventions
The Education Endowment Foundation looked at the benefits of targeted maths interventions, for students aged 3-7. Their report outlines the key features that make good interventions work well.
“Consider the following to make the most of targeted support:
- use more experienced staff to support children with the greatest needs
- provide training and support for staff using targeted activities, including structured resources or activity plans with clear objectives
- sessions should be brief and regular
- quality is generally more important than quantity— there is some evidence to suggest that time-limited interventions may be more effective
- make explicit connections between targeted support and everyday activities or teaching; practitioners delivering additional support should have time to discuss this work with their colleagues.”
- Clark, Henderson, & Gifford, 2020(68)
Real-life strategies
|
We heard from teachers and school leaders that it works well to… |
|
Provide short-term interventions with a specific focus. One school ERO visited emphasised that it is the responsibility of classroom teachers to identify students that need extra help. When teachers become concerned about progress, the school moves quickly to put a structured programme in place. A common intervention at this school is for teacher aides who are trained in a targeted maths intervention to run a 15-minute structured intervention programme during the class maths lesson. These sessions are linked back to the content of the main session. The students in the intervention group join their peers for the majority of maths time. |
|
Offer students additional optional workshops in class as a follow-up. We observed teachers who introduce a task or maths concept to a larger group, and then check with students about their level of confidence. They then offer opportunities for students to stay back, join an additional workshop, or have one-to-one teacher support if they choose to. The follow-up activity sometimes involves working more deliberately through the original task with added materials, explanations, and diagrams. Teachers provide additional opportunities for students to talk about and show their ideas as they tackle similar tasks. |
|
Provide additional maths sessions. Schools sometimes supplement their current programme with additional sessions for students who are struggling. These sessions use familiar games and activities to practise using their skills and building their knowledge. For example, playing a board game to focus students on accurately counting forward or backward, or to practise basic facts to ten. These sessions focus strongly on consolidating learning, the accurate use of maths vocabulary, and sometimes introducing ideas that they are about to encounter in their classroom maths. |
|
Support from teacher aides |
|
ERO research shows that - unless the teacher aide has appropriate specialist qualifications to do so - it is not good practice for teacher aides to be the main people that plan for students that need extra support. The evidence is clear that this contributes to poorer outcomes for those students. Instead, it should be qualified teachers that adapt and oversee the learning of those students. A great alternative to traditional ‘velcro’ teacher aide support is for teacher aides to work across the wider class, rotating support for all students on their maths tasks based on discussions with the classroom teacher. This enables teachers to work more regularly with those students that need extra support in maths, which has proven benefits for these students. As a general rule of thumb, teachers should spend at least as much time supporting students that need targeted support as they do with the rest of the class. While teacher aides should not have overall responsibility for students’ programmes, tasks, or assessments, they can have a supportive role in the delivery of structured maths interventions. However, this only works when teacher aides deliver interventions as instructed, based on robust training, with a highly structured approach. Research shows that when teacher aides don’t use the intended structure – for example, not using resources, or condensing several short sessions into one long one – this has a negative impact on student learning. Teachers can help teacher aides do their best work through lots of communication, robust training, and careful timetabling, so that structured intervention sessions link to classroom maths learning. These sessions might occur within the classroom, for example, while all students are working in small groups. Teachers can also support teacher aides to develop and fine-tune their intervention delivery practices through professional discussions, observations, and modelling. Discussions should include clarifying why a maths intervention was chosen for a particular student – talking about the evidence base, or the assessments that led to this decision. This helps teacher aides to buy in to the ‘how and why’ of the intervention. For more about teachers and teacher aides working together, see A practical guide for teachers: What quality teacher aide practice looks like (ero.govt.nz)(69) |
Programme example: Accelerated Learning in Mathematics (ALiM)
Accelerating Learning in Mathematics (ALiM) is a Ministry of Education initiative used commonly in Aotearoa New Zealand schools. The programme is designed to lift achievement in maths for students in Years 1-10 who have fallen behind the achievement level of their peers. ALiM is designed as a short-term intervention to be used in addition to a school’s regular maths programme. Teachers complete “cycles of inquiry” focused on accelerating the achievement levels of target students, increasing the rate of their learning to reach the level of their peers.(70) Schools decide the timing and length of these cycles for themselves. An ALiM session might see teachers introduce activities that, for the majority of students in the class, can be done with minimum teacher intervention. When this is working well, most students are undertake targeted maths tasks that are both engaging and meaningful, and the teacher is freed up to help students that require extra support.(71) A key feature of the ALiM programme is partnering with families/whānau to support maths learning.(72)
d) Teachers support competent maths students through adding challenge and complexity
Research shows that highly capable students are at risk of disengagement from learning - similar to their peers who need support to build foundational learning skills and knowledge. Students who demonstrate a very strong capability in maths require attentive and targeted support, so that they have equitable opportunities to make progress at school just like their peers are able to.
“Without appropriate challenge, gifted students are ‘at risk’; they may demonstrate boredom, loss of interest in or commitment to mathematics, limited metacognition, and poor behaviour.”
- Diezmann & Watters, 1997(73)
Teachers need to be well-equipped and confident with a range of extra-challenge strategies to support these students engaging in maths learning alongside (rather than in isolation from) their peers. Strategies may involve enriching, extending, or accelerating their learning through complex and challenging tasks, or providing additional experiences or materials and representations. Some teachers will need support to build these practices, and will benefit from working with curriculum leaders or seeking external support.
Real-life strategies
|
We heard from teachers and school leaders that it works well to… |
|
Use assessments to be clear and specific about learning levels. Assessments should be used to identify the need for targeted action. Teachers use a combination of formal (using tools) and informal assessment. This helps teachers to be clear and specific about students’ level of understanding, and where targeted challenge is needed. For example, we saw teachers observe students’ levels of engagement and interest during maths sessions, whether they complete tasks very quickly or at a superficial level, and whether they exhibit off-task behaviours. |
|
Add challenge and complexity to classroom tasks (‘problematisation’ of tasks). Teachers find ways to modify or add challenge to class tasks for their able students. For example: When doing a warm-up activity counting from 19, a teacher provides additional challenge by asking students to count from 119, or 3019. (See the box below for more about problematisation.) |
|
Providing ‘challenging tasks’ and investigations. Providing ‘challenging tasks’ (see the box below) is an effective strategy for supporting students to engage more fully in maths sessions along with their peers, while expanding their knowledge and understanding. For example, a class investigation involving measurement and statistics allows students who are competent in measurement and graphing concepts to show leadership, and to apply and extend their knowledge and skills. They support their peers to investigate how the length of shadows change throughout the day. They collaborate in groups of three to measure their shadows in the playground. They record this information in their books, and then decide how best to present the information for others to understand. Note: Mathematical investigations are where students use their maths understanding in various situations. Investigations often begin with a 'real world' mathematical question and allow for a range of approaches or solutions. |
Tips for engaging students who require additional challenge
There are some key things teachers can do to help students who require additional challenge to engage more fully in maths.
These include:
- minimising time spent memorising facts or practising skills that are already mastered
- delaying direct teacher support so that students have sufficient opportunity to work with maths problems, encounter the complexities in tasks, and test and talk through their own approaches with peers
- asking students to record explanations and reflect on their thinking
- encouraging students to work with peers to share their ideas and learn from others
- ensuring each whole-class activity offers opportunities for competent students to draw on a wide range of knowledge and find additional solutions
- inviting students to communicate their solutions and offering feedback to refine their strategies and ideas
- ensuring they aren’t just ‘left to it’ during maths time. Teachers should allow space, but remember to check in with students. This might involve timely suggestions, prompting questions, engaging in debate, reminders of relevant learning or knowledge, or provision of carefully considered resources, materials, and representations.
What are challenging tasks?
Challenging tasks (also called “rich tasks‟) are complex maths problems that don’t have a single or obvious answer. Students are not initially aware of how to solve the task and have to invent mathematical actions to solve it.
These sorts of tasks enhance motivation and help students to develop confidence, capability, and curiosity (“mathematical power”(74)) through high-level thinking and reasoning. Such tasks also encourage metacognitive skills, helping students understand and develop control over how they are thinking.(75)
Challenging tasks are complex and absorbing mathematical problems that:
- require students to process multiple pieces of mathematical information at the same time and make connections between them
- have more than one possible solution or solution method
- involve more than one mathematical step
- are perceived as both engaging and challenging by students.
What is problematisation?
Problematisation is when an existing maths task is adjusted by the teacher to be more complex or challenging. Methods for problematisation can include “inserting obstacles to the solutions, removing some information, or requiring students to use particular representations or develop generalisations.”(76) Younger students in particular benefit from adjusted maths games and more access to manipulative tools and equipment.
“The construction of a number line to represent the distance of the ten brightest stars. This required the application of knowledge of large numbers, relative magnitude, and scale—and extension of the more typical use of the number line to represent sets of numbers.”
- Diezmann & English, 2001a
2) Good practice example
One school ensures they provide additional support or targeted teaching for all their students within the classroom by including teacher aides as part of their daily programme. The teacher aides participate in maths professional learning sessions alongside teachers and are fully informed about the maths ideas included in each lesson. This includes understanding the maths embedded in the games, and how to highlight and support students to access these.
The teacher aides are active in the lessons, working alongside teachers to offer support to identified students in the context of the various parts of the programme. Sometimes this includes helping them to use materials to solve a problem, or supporting them as they work alongside a partner or participate in a larger group. Teachers help the student to use the knowledge they have, understand and use maths vocabulary, or learn how to play a game which supports their skill development.
5) Reflective questions for teachers
- Am I noticing disengagement, or lack of confidence or progress in any of my students?
- Do I know if this is because the student finds the maths learning too easy or too hard?
- If too hard – are there alternative approaches, materials, or representations I could try? Are there some negative learning experiences influencing their engagement, or learning needs or disabilities to take account of?
- If too easy – do students have enough opportunities to grapple with authentic, complex, or challenging tasks?
- Have I spoken to this student about what they think?
Practice area 5: Teachers use tools and representations to express mathematical concepts
This practice area is about intentionally using diagrams, models, and equipment to support learning about mathematical ideas.
When this is going well, teachers are purposeful about how and why they use different tools and representations. They are confident about supporting students to use them to solve tasks and show their thinking. Teachers also make sure that students have regular opportunities to work with a variety of materials and use them freely to express their ideas.
In this section, we set out why tools and representations are essential for Year 1-3 students, the importance of careful planning and selection in making links to maths concepts, and how to support students to use tools and representations well. We also offer practical guidance on how teachers can put this into practice in their own classrooms.
Overview of this section
This part of the report sets out useful information about using tools and representations for supporting maths learning in Years 1-3. It includes:
- What is this practice area?
- Why is this important?
- What does good practice look like in real life?
- Good practice example
- Reflective questions for teachers
1) What is this practice area?
Tools and representations are used to help students understand important maths ideas. Teachers use a range of materials, specialised equipment, diagrams, and symbols as they introduce or reinforce maths concepts. They model how to use and apply tools and representations, supporting students to understand and express ideas related to the concepts being taught. An important aspect of this practice area is making sure that students develop familiarity with tools and representations and have regular access to a range of them to help solve tasks and explain their thinking.
The key teaching practices discussed in this section are:
- teachers plan how to use tools and representations, based on a clear rationale
- teachers make clear links between maths concepts and the tools and representations they are using
- teachers encourage students to use or adapt tools and representations to express their maths ideas.
“The teacher lets us use materials like blocks and place value boards.” – Student
Examples of tools and representations
There are a wide range of maths tools and representations available to teachers, including physical objects, visual representations, and symbols.
Physical objects can include:
- everyday objects from the student’s world (e.g., shells, stones, toy cars)
- specialised mathematics equipment (e.g., abacus, hundreds boards, place value blocks, fraction kits)
- grouped objects or structures for organising objects (e.g., bags of 10 objects, 10s frames, place value houses).
Visual representations use pictures to show maths ideas. These include diagrams, digital models, photographs, multiplication arrays, number lines, tables, graphs, digital models of 3-D shapes, probability tests etc.
Symbols (such as numerals, operation signs, fractions, equations etc.) are abstract, containing hidden meanings, and should be used alongside other tools and representations.
2) Why is this important?
Mathematics is highly abstract, and students need good support to be able to make sense of these abstract ideas. Providing deliberate strategies for making these links is a key part of the teacher’s role. Evidence shows that tools and representations help young students to build their mental models of key maths concepts and processes, by making connections to the physical (‘real’) world.(77) For young students in particular, a hands-on approach is effective for understanding complex ideas.(78) Tools and representations connect maths with the ‘real world’ at a crucial time.
The use of equipment, diagrams, and symbols connects to students’ experiences of play – for example, young students may first encounter maths representations as they play with blocks, group or categorise objects, or count fingers to show numbers. Using their bodies to physically interact with equipment or space helps them to make mental connections between maths concepts and their lived experience. In another example, physical movements such as jumping or stepping along a number line can help to build knowledge of number sequences, or make the processes of addition or subtraction visible – making it ‘real’.
Teachers can support students to use tools and representations purposefully to communicate, explain, and justify their maths thinking.(79) This enables them to test and extend their understanding of abstract ideas.(80) As students manipulate tools and representations, teachers can also monitor students’ levels of understanding, their progress, and address any developing misconceptions.
It is critical that students at the beginning of their school years are supported to build mental models which are reliable and accurate, so that they can continue to build on these foundations in their ongoing learning.(81) This is essential for helping students transfer their learning about concepts and apply them to new situations and contexts when solving problems.
“If you get stuck on things, [the teacher] gives us something to help us like a pattern we know, but have forgotten about. She shows us a way to work it out (or) she might give us materials to help us.” - Student
What do we mean by ‘abstract’?
In this section, we talk a lot about making sense of ‘abstract’ ideas. Broadly, this means maths ideas that are hard to explain or understand without seeing or experiencing them a few times, and in different contexts. Diagrams, materials, and symbols provide ways to represent or model these ideas to help students build a mental picture.
As an example, even the key idea of a number is abstract. ‘Five’ doesn’t make a lot of sense without experiencing what it means in real life. To understand ‘five’ or ‘fiveness’ (cardinality), students needs to experience the consistency of ‘five’ across several experiences with different representations of five – five fingers, five peas, five dots, five children... Fiveness will be the same whether they are looking at a group of five cats, as well as a mixed group of five cats and dogs. Having a range of visual or physical experiences helps students to understand the meaning of the abstract idea of five.
Measurement is also an abstract idea - repeating the use of close-fitting units to talk about or compare objects. To build the understanding of that abstract concept, students use informal units (e.g., body parts) or formal tools (such as rulers, cubes, or measuring cups) to measure a length, area, or the capacity of an object. This helps the student connect their ‘real’ experience to the abstract concept of measurement.
3) What does good practice look like in real life?
As part of this study, we talked to teachers and school leaders about the strategies that have worked well in their experience. We’ve collected their ideas and strategies here. It is important to reflect carefully about which of these will benefit each school’s unique community and context. No strategies are one-size-fits-all so all these strategies won’t be the right fit for everyone.
The key teacher practices that we focus on are:
- teachers plan how to use tools and representations, based on a clear rationale
- teachers make clear links between maths concepts and tools and representations
- teachers encourage students to use or adapt tools and representations to express their maths ideas.
a) Teachers plan how to use tools and representations, based on a clear rationale
Teachers’ preparation for a maths teaching session needs to include careful identification of the best tools and representations for showing a maths idea. It is crucial that teachers are really clear about how and why specific tools and representations are used for particular lessons. Teachers need to also consider the limitations of their tools and representations and how they will use them, so that they can use them in ways that won’t be confusing for students.
Teachers need to be familiar with the range of materials available to them, think carefully about the best materials to introduce or reinforce underlying maths concepts, and be confident about using them.(82) This will often involve drawing on subject knowledge expertise, gained through connecting with experienced peers and curriculum leaders, or formalised professional learning.
All of this means being prepared: planning ahead for the different materials that could be required, and anticipating the different ways students may use those materials. Doing this thinking ahead of time means teachers can be ready to respond in the moment, and expand on new ideas if students present them.
“We make do with what we have, even if it’s a bucket of conkers.”
- Teacher
Thinking about which tools to use
Teachers need to think carefully about which tools and representations are right for the job.
For example, when preparing a lesson about multiplication, teachers should consider how to connect to students’ prior learning and the mental images they have built through previous learning experiences. For example: have they been looking at the area of a rectangle (an array)? Have they been working with models which show multiple groups of the same size (repeated addition)? These are important considerations when making a choice between using materials which help them connect multiplication to an array (as in an arrangement of 5 x 4 cookies on a tray) or counters grouped in sets (5 groups of 4).
When planning a lesson for fractions, teachers should consider that it is difficult to show the ‘equal part’ aspect of fractions using a freestyle drawing of a cake, because the pieces won’t quite look even. Similarly, using groups of counters to show fractions won’t clearly show how they relate to ‘parts of a whole’. Counting to 40 on a number line does not show the ‘quantity’ of the number as well as an abacus, or sticks grouped in bundles of 10.
Real-life strategies
|
We heard from teachers and school leaders that it works well to… |
|
Reflect on suitability of the equipment for these specific students. We heard that teachers consider whether the equipment is familiar or unfamiliar to the class, if it has been used for alternative purposes, or whether the equipment might present confusing or distracting information. Doing this thinking ahead of time supports teachers to know whether a particular tool is the right fit. |
|
Prepare simple materials in advance, that link to planned lessons. In preparation for a Year 2 lesson, a teacher prints large numbers, arrows, and mathematical concept words. In class, the teacher uses these materials to build students’ understanding of number sequences to 20. She supports students to focus on mathematical words by arranging numbers and pointing arrows towards the words ‘before’ and ‘after’. She asks prompting questions, like: “What is the next number after 5? What is a number which comes before 19?” |
|
Have a wider than necessary range of tools ready, so that lessons can be adapted in response to students. One teacher plans a lesson for a Year 2 group which looks at dividing 24 counters into four groups – but also has fraction strips, an abacus, and multiplication arrays handy. This helps her to reinforce the learning for some students by modelling connections to fractions, repeated addition, multiplication, and division. Writing equipment is also on hand to record the equations or draw diagrams as students talk about their ideas. |
|
Share knowledge with other teachers about limitations of tools and materials, to support consistency across classrooms. One school has developed a ‘guide’ for teachers to show ways that materials can be used to demonstrate different mathematical ideas. It includes sections on how to use materials, which tools are best for specific topics or concepts (e.g., fractions), and the benefits of using each of the materials for young students. |
b) Teachers make clear links between maths concepts and tools and representations
Students benefit from teachers being explicit about the use of tools and representations. This will often begin with modelling of processes or worked examples and clear instructions from the teacher. Regular use and follow-up sessions can support students to understand the purpose and use of materials and make connections between concepts. Making maths equipment available for students to access independently can also support students to build familiarity with how they can be used.
Real-life strategies
|
We heard from teachers and school leaders that it works well to… |
|
Introduce tools and equipment in other contexts (e.g., construction, games, or other play-related activities). Teachers introduce materials in independent play or group activities, for example, sorting shells by colour or size during a game, before using them to demonstrate addition or subtraction in an explicit teaching session. |
|
Use digital tools to support individual or peer learning. In many classes, students access individual digital devices for independent or small group activities. They continue to work on a task independently or in pairs, similar to a worked example, but without direct support from the teacher. We heard that this works well to enable students to apply and practise new learning, and consolidate ideas. |
|
Provide a wide selection of materials relevant to one concept, to support students to make links across tools and representations. For example, the range of materials made available for an opening maths activity about a ‘number of the day’ in one Year 2 classroom included: • an abacus for skip-counting in 5s • a hundreds board for skip-counting in 10s and for ‘number of the day’ activities • big printed numbers which students arrange in order • printed words and arrows. |
|
Use memory games to help students talk about maths ideas. For example, one Year 1-2 group works with the teacher who shows an image of gingerbread ‘men’ on the screen for 5-10 seconds before disappearing. Each gingerbread man has two buttons. The students are then asked to ‘turn and talk’ to their buddies. Questions for students include, “How many gingerbread men were there? How did you get that answer? How many buttons were there? If there was another gingerbread man, how many buttons would there be?” |
|
Look for opportunities to reinforce previous maths learning as students engage in other maths activities. For example, a teacher uses a counting activity as an opportunity to revisit and build on prior learning. Using an abacus (coloured beads to 100) and hundreds board when counting between 1 and 20, the teacher draws attention to:
|
|
Use large screens to quickly access and share symbols and images. Many classes use large screens to show photographs or images for whole-class and small group activities. In other classes, the large screen is used in a warm-up activity where students are asked to look at number or spatial patterns in photographs, with teachers asking, “What do you notice?” |
|
Short story: Using digital technology alongside other materials |
|
In an inner-city school, teachers integrate digital tools and other physical materials into their maths lessons to present, extend, and reinforce learning – and act as a record of learning. Year 1 students work at a table which includes egg containers, counters, and an abacus to model different ways to show ‘10’. This is an opportunity for practising or reinforcing knowledge as they work independently to represent the same thing in different ways. Students use their devices to take photos of their work and voice record their thinking to place on their individual digital platform. This is later accessed by the teacher so they can monitor or assess each student’s learning, or to share the presentation with the class. These posts can also be shared with parents/whānau through a digital portal to show and celebrate their learning. |
C) Teachers encourage students to use or adapt tools and representations to express their maths ideas
Students deepen their maths knowledge when they make connections between different tools and representations. For example, there are different representations of a number: the digit ‘4’, or written out ‘four’, or represented with counters ‘••••’. Finding ways to show these ideas through representations helps students to make connections between the different experiences and grow a fuller understanding.
Initially, a student might express their understanding of a concept by drawing, or by using their fingers. As they grow more familiar with more tools and representations, they have a broader range of options for expressing maths ideas. Deliberate teacher support through prompting and encouragement supports students to get the most out of materials.
“Materials, materials, materials! It’s really important that we have things that are tactile, that are very well-known to the children.” – Teacher
“Maths is more my favourite subject – I’m really top at it. It’s just my thing. I like measurement – sometimes I’m curious about how long things are in my house, and I measure them with paper or something.” – Student
Real-life strategies
|
We heard from teachers and school leaders that it works well to… |
|
Model how to use different materials to support students’ thinking. For example, a teacher demonstrates to students how to use their hands to show 7, and make connections to ‘flystrips’ to show 5 + 2. |
|
Monitor how students work with materials and representations, and adjust as necessary. Teachers pause their lessons to provide instruction about how to use the materials correctly, or provide an alternative tool when it becomes clear through their use of equipment that students do not yet have a clear understanding of the intended concept. In one observation, a teacher works with a small group to write and show numbers with three or more digits. She abandons the use of place value houses when students are confused about how to say the numbers, and moves to less abstract representations instead. To better show how the 8 in the number 386 she demonstrates the number 86 on the abacus and bundles of ten: as 8 rows of ten and 6 ones, and 8 bundles of ten and 6 ones. The teacher then brings the discussion back to the place value house diagram and written numeral. |
|
Observe the students’ choice of tools and materials. In one class, students are encouraged to select their own materials from a range of options to solve a maths problem. The teacher explains that as students make their selection, it boosts students’ responsibility for their own learning, and also shows the teacher how well the students have understood the task. |
4) Good practice example
In a warm-up activity, a teacher moves between different representations to illustrate underlying place value concepts in the number 34. Initially she uses an abacus with the class to support the count to 34. She then shows the class that there are three rows of 10 and four ones on the abacus, and then switched to show that similar patterns exist on the hundreds board.
Later, in response to a student’s question, she uses sticks and bundles of ten to count out the number. These materials are then used alongside place value charts to reinforce the ideas that being discussed.
In a follow-up activity, students work in small groups to use a wide range of materials (such as number lines, bundles of sticks, place value blocks, place value houses, equations) to show the ‘number of the day’ (34) on a laminated chart.
5) Reflective questions for teachers
- When preparing a lesson, do I always think carefully about which equipment would best show the idea I am trying to get across? How about planning for other concepts that I can reinforce or incorporate?
- Do my students have regular access to a range of materials, to support their thinking when working on tasks? Are they encouraged to illustrate their thinking with these materials?
- Do I ensure that students have opportunities to explore new materials, before using them in a maths task?
- Am I confident about which representations and materials are most accurate in illustrating a concept and minimise the opportunity for developing misconceptions? Do I need to seek support?
- After lessons, do I deliberately reflect about which tools and representations seemed to resonate best with students? What additional materials or representations could we use next time?
This practice area is about intentionally using diagrams, models, and equipment to support learning about mathematical ideas.
When this is going well, teachers are purposeful about how and why they use different tools and representations. They are confident about supporting students to use them to solve tasks and show their thinking. Teachers also make sure that students have regular opportunities to work with a variety of materials and use them freely to express their ideas.
In this section, we set out why tools and representations are essential for Year 1-3 students, the importance of careful planning and selection in making links to maths concepts, and how to support students to use tools and representations well. We also offer practical guidance on how teachers can put this into practice in their own classrooms.
Overview of this section
This part of the report sets out useful information about using tools and representations for supporting maths learning in Years 1-3. It includes:
- What is this practice area?
- Why is this important?
- What does good practice look like in real life?
- Good practice example
- Reflective questions for teachers
1) What is this practice area?
Tools and representations are used to help students understand important maths ideas. Teachers use a range of materials, specialised equipment, diagrams, and symbols as they introduce or reinforce maths concepts. They model how to use and apply tools and representations, supporting students to understand and express ideas related to the concepts being taught. An important aspect of this practice area is making sure that students develop familiarity with tools and representations and have regular access to a range of them to help solve tasks and explain their thinking.
The key teaching practices discussed in this section are:
- teachers plan how to use tools and representations, based on a clear rationale
- teachers make clear links between maths concepts and the tools and representations they are using
- teachers encourage students to use or adapt tools and representations to express their maths ideas.
“The teacher lets us use materials like blocks and place value boards.” – Student
Examples of tools and representations
There are a wide range of maths tools and representations available to teachers, including physical objects, visual representations, and symbols.
Physical objects can include:
- everyday objects from the student’s world (e.g., shells, stones, toy cars)
- specialised mathematics equipment (e.g., abacus, hundreds boards, place value blocks, fraction kits)
- grouped objects or structures for organising objects (e.g., bags of 10 objects, 10s frames, place value houses).
Visual representations use pictures to show maths ideas. These include diagrams, digital models, photographs, multiplication arrays, number lines, tables, graphs, digital models of 3-D shapes, probability tests etc.
Symbols (such as numerals, operation signs, fractions, equations etc.) are abstract, containing hidden meanings, and should be used alongside other tools and representations.
2) Why is this important?
Mathematics is highly abstract, and students need good support to be able to make sense of these abstract ideas. Providing deliberate strategies for making these links is a key part of the teacher’s role. Evidence shows that tools and representations help young students to build their mental models of key maths concepts and processes, by making connections to the physical (‘real’) world.(77) For young students in particular, a hands-on approach is effective for understanding complex ideas.(78) Tools and representations connect maths with the ‘real world’ at a crucial time.
The use of equipment, diagrams, and symbols connects to students’ experiences of play – for example, young students may first encounter maths representations as they play with blocks, group or categorise objects, or count fingers to show numbers. Using their bodies to physically interact with equipment or space helps them to make mental connections between maths concepts and their lived experience. In another example, physical movements such as jumping or stepping along a number line can help to build knowledge of number sequences, or make the processes of addition or subtraction visible – making it ‘real’.
Teachers can support students to use tools and representations purposefully to communicate, explain, and justify their maths thinking.(79) This enables them to test and extend their understanding of abstract ideas.(80) As students manipulate tools and representations, teachers can also monitor students’ levels of understanding, their progress, and address any developing misconceptions.
It is critical that students at the beginning of their school years are supported to build mental models which are reliable and accurate, so that they can continue to build on these foundations in their ongoing learning.(81) This is essential for helping students transfer their learning about concepts and apply them to new situations and contexts when solving problems.
“If you get stuck on things, [the teacher] gives us something to help us like a pattern we know, but have forgotten about. She shows us a way to work it out (or) she might give us materials to help us.” - Student
What do we mean by ‘abstract’?
In this section, we talk a lot about making sense of ‘abstract’ ideas. Broadly, this means maths ideas that are hard to explain or understand without seeing or experiencing them a few times, and in different contexts. Diagrams, materials, and symbols provide ways to represent or model these ideas to help students build a mental picture.
As an example, even the key idea of a number is abstract. ‘Five’ doesn’t make a lot of sense without experiencing what it means in real life. To understand ‘five’ or ‘fiveness’ (cardinality), students needs to experience the consistency of ‘five’ across several experiences with different representations of five – five fingers, five peas, five dots, five children... Fiveness will be the same whether they are looking at a group of five cats, as well as a mixed group of five cats and dogs. Having a range of visual or physical experiences helps students to understand the meaning of the abstract idea of five.
Measurement is also an abstract idea - repeating the use of close-fitting units to talk about or compare objects. To build the understanding of that abstract concept, students use informal units (e.g., body parts) or formal tools (such as rulers, cubes, or measuring cups) to measure a length, area, or the capacity of an object. This helps the student connect their ‘real’ experience to the abstract concept of measurement.
3) What does good practice look like in real life?
As part of this study, we talked to teachers and school leaders about the strategies that have worked well in their experience. We’ve collected their ideas and strategies here. It is important to reflect carefully about which of these will benefit each school’s unique community and context. No strategies are one-size-fits-all so all these strategies won’t be the right fit for everyone.
The key teacher practices that we focus on are:
- teachers plan how to use tools and representations, based on a clear rationale
- teachers make clear links between maths concepts and tools and representations
- teachers encourage students to use or adapt tools and representations to express their maths ideas.
a) Teachers plan how to use tools and representations, based on a clear rationale
Teachers’ preparation for a maths teaching session needs to include careful identification of the best tools and representations for showing a maths idea. It is crucial that teachers are really clear about how and why specific tools and representations are used for particular lessons. Teachers need to also consider the limitations of their tools and representations and how they will use them, so that they can use them in ways that won’t be confusing for students.
Teachers need to be familiar with the range of materials available to them, think carefully about the best materials to introduce or reinforce underlying maths concepts, and be confident about using them.(82) This will often involve drawing on subject knowledge expertise, gained through connecting with experienced peers and curriculum leaders, or formalised professional learning.
All of this means being prepared: planning ahead for the different materials that could be required, and anticipating the different ways students may use those materials. Doing this thinking ahead of time means teachers can be ready to respond in the moment, and expand on new ideas if students present them.
“We make do with what we have, even if it’s a bucket of conkers.”
- Teacher
Thinking about which tools to use
Teachers need to think carefully about which tools and representations are right for the job.
For example, when preparing a lesson about multiplication, teachers should consider how to connect to students’ prior learning and the mental images they have built through previous learning experiences. For example: have they been looking at the area of a rectangle (an array)? Have they been working with models which show multiple groups of the same size (repeated addition)? These are important considerations when making a choice between using materials which help them connect multiplication to an array (as in an arrangement of 5 x 4 cookies on a tray) or counters grouped in sets (5 groups of 4).
When planning a lesson for fractions, teachers should consider that it is difficult to show the ‘equal part’ aspect of fractions using a freestyle drawing of a cake, because the pieces won’t quite look even. Similarly, using groups of counters to show fractions won’t clearly show how they relate to ‘parts of a whole’. Counting to 40 on a number line does not show the ‘quantity’ of the number as well as an abacus, or sticks grouped in bundles of 10.
Real-life strategies
|
We heard from teachers and school leaders that it works well to… |
|
Reflect on suitability of the equipment for these specific students. We heard that teachers consider whether the equipment is familiar or unfamiliar to the class, if it has been used for alternative purposes, or whether the equipment might present confusing or distracting information. Doing this thinking ahead of time supports teachers to know whether a particular tool is the right fit. |
|
Prepare simple materials in advance, that link to planned lessons. In preparation for a Year 2 lesson, a teacher prints large numbers, arrows, and mathematical concept words. In class, the teacher uses these materials to build students’ understanding of number sequences to 20. She supports students to focus on mathematical words by arranging numbers and pointing arrows towards the words ‘before’ and ‘after’. She asks prompting questions, like: “What is the next number after 5? What is a number which comes before 19?” |
|
Have a wider than necessary range of tools ready, so that lessons can be adapted in response to students. One teacher plans a lesson for a Year 2 group which looks at dividing 24 counters into four groups – but also has fraction strips, an abacus, and multiplication arrays handy. This helps her to reinforce the learning for some students by modelling connections to fractions, repeated addition, multiplication, and division. Writing equipment is also on hand to record the equations or draw diagrams as students talk about their ideas. |
|
Share knowledge with other teachers about limitations of tools and materials, to support consistency across classrooms. One school has developed a ‘guide’ for teachers to show ways that materials can be used to demonstrate different mathematical ideas. It includes sections on how to use materials, which tools are best for specific topics or concepts (e.g., fractions), and the benefits of using each of the materials for young students. |
b) Teachers make clear links between maths concepts and tools and representations
Students benefit from teachers being explicit about the use of tools and representations. This will often begin with modelling of processes or worked examples and clear instructions from the teacher. Regular use and follow-up sessions can support students to understand the purpose and use of materials and make connections between concepts. Making maths equipment available for students to access independently can also support students to build familiarity with how they can be used.
Real-life strategies
|
We heard from teachers and school leaders that it works well to… |
|
Introduce tools and equipment in other contexts (e.g., construction, games, or other play-related activities). Teachers introduce materials in independent play or group activities, for example, sorting shells by colour or size during a game, before using them to demonstrate addition or subtraction in an explicit teaching session. |
|
Use digital tools to support individual or peer learning. In many classes, students access individual digital devices for independent or small group activities. They continue to work on a task independently or in pairs, similar to a worked example, but without direct support from the teacher. We heard that this works well to enable students to apply and practise new learning, and consolidate ideas. |
|
Provide a wide selection of materials relevant to one concept, to support students to make links across tools and representations. For example, the range of materials made available for an opening maths activity about a ‘number of the day’ in one Year 2 classroom included: • an abacus for skip-counting in 5s • a hundreds board for skip-counting in 10s and for ‘number of the day’ activities • big printed numbers which students arrange in order • printed words and arrows. |
|
Use memory games to help students talk about maths ideas. For example, one Year 1-2 group works with the teacher who shows an image of gingerbread ‘men’ on the screen for 5-10 seconds before disappearing. Each gingerbread man has two buttons. The students are then asked to ‘turn and talk’ to their buddies. Questions for students include, “How many gingerbread men were there? How did you get that answer? How many buttons were there? If there was another gingerbread man, how many buttons would there be?” |
|
Look for opportunities to reinforce previous maths learning as students engage in other maths activities. For example, a teacher uses a counting activity as an opportunity to revisit and build on prior learning. Using an abacus (coloured beads to 100) and hundreds board when counting between 1 and 20, the teacher draws attention to:
|
|
Use large screens to quickly access and share symbols and images. Many classes use large screens to show photographs or images for whole-class and small group activities. In other classes, the large screen is used in a warm-up activity where students are asked to look at number or spatial patterns in photographs, with teachers asking, “What do you notice?” |
|
Short story: Using digital technology alongside other materials |
|
In an inner-city school, teachers integrate digital tools and other physical materials into their maths lessons to present, extend, and reinforce learning – and act as a record of learning. Year 1 students work at a table which includes egg containers, counters, and an abacus to model different ways to show ‘10’. This is an opportunity for practising or reinforcing knowledge as they work independently to represent the same thing in different ways. Students use their devices to take photos of their work and voice record their thinking to place on their individual digital platform. This is later accessed by the teacher so they can monitor or assess each student’s learning, or to share the presentation with the class. These posts can also be shared with parents/whānau through a digital portal to show and celebrate their learning. |
C) Teachers encourage students to use or adapt tools and representations to express their maths ideas
Students deepen their maths knowledge when they make connections between different tools and representations. For example, there are different representations of a number: the digit ‘4’, or written out ‘four’, or represented with counters ‘••••’. Finding ways to show these ideas through representations helps students to make connections between the different experiences and grow a fuller understanding.
Initially, a student might express their understanding of a concept by drawing, or by using their fingers. As they grow more familiar with more tools and representations, they have a broader range of options for expressing maths ideas. Deliberate teacher support through prompting and encouragement supports students to get the most out of materials.
“Materials, materials, materials! It’s really important that we have things that are tactile, that are very well-known to the children.” – Teacher
“Maths is more my favourite subject – I’m really top at it. It’s just my thing. I like measurement – sometimes I’m curious about how long things are in my house, and I measure them with paper or something.” – Student
Real-life strategies
|
We heard from teachers and school leaders that it works well to… |
|
Model how to use different materials to support students’ thinking. For example, a teacher demonstrates to students how to use their hands to show 7, and make connections to ‘flystrips’ to show 5 + 2. |
|
Monitor how students work with materials and representations, and adjust as necessary. Teachers pause their lessons to provide instruction about how to use the materials correctly, or provide an alternative tool when it becomes clear through their use of equipment that students do not yet have a clear understanding of the intended concept. In one observation, a teacher works with a small group to write and show numbers with three or more digits. She abandons the use of place value houses when students are confused about how to say the numbers, and moves to less abstract representations instead. To better show how the 8 in the number 386 she demonstrates the number 86 on the abacus and bundles of ten: as 8 rows of ten and 6 ones, and 8 bundles of ten and 6 ones. The teacher then brings the discussion back to the place value house diagram and written numeral. |
|
Observe the students’ choice of tools and materials. In one class, students are encouraged to select their own materials from a range of options to solve a maths problem. The teacher explains that as students make their selection, it boosts students’ responsibility for their own learning, and also shows the teacher how well the students have understood the task. |
4) Good practice example
In a warm-up activity, a teacher moves between different representations to illustrate underlying place value concepts in the number 34. Initially she uses an abacus with the class to support the count to 34. She then shows the class that there are three rows of 10 and four ones on the abacus, and then switched to show that similar patterns exist on the hundreds board.
Later, in response to a student’s question, she uses sticks and bundles of ten to count out the number. These materials are then used alongside place value charts to reinforce the ideas that being discussed.
In a follow-up activity, students work in small groups to use a wide range of materials (such as number lines, bundles of sticks, place value blocks, place value houses, equations) to show the ‘number of the day’ (34) on a laminated chart.
5) Reflective questions for teachers
- When preparing a lesson, do I always think carefully about which equipment would best show the idea I am trying to get across? How about planning for other concepts that I can reinforce or incorporate?
- Do my students have regular access to a range of materials, to support their thinking when working on tasks? Are they encouraged to illustrate their thinking with these materials?
- Do I ensure that students have opportunities to explore new materials, before using them in a maths task?
- Am I confident about which representations and materials are most accurate in illustrating a concept and minimise the opportunity for developing misconceptions? Do I need to seek support?
- After lessons, do I deliberately reflect about which tools and representations seemed to resonate best with students? What additional materials or representations could we use next time?
Practice area 6: The classroom learning environment encourages mathematical thinking, collaboration, and the enjoyment of maths
This practice area is about teachers setting up the classroom to encourage students’ maths thinking and maths participation.
When this is going well, the classroom is visibly rich in maths content and materials. Teachers organise the class and classroom in ways that help students to engage with maths tasks and work collaboratively. Classroom rules and expectations support students to share ideas, ask questions, and participate in mathematical discussion and debate.
In this section, we describe why the classroom learning environment is important for encouraging mathematical thinking. We also offer practical guidance on how teachers can grow this practice within their own class.
Overview of this section
This part of the report sets out useful information about how teachers can set up their learning environment so that its supports mathematical thinking and enjoyment of maths. It includes:
- What is this practice area?
- Why is this important?
- What does good practice look like in real life?
- Good practice example
- Reflective questions for teachers
1) What is this practice area?
This practice area is about teachers understanding their students well, and taking action to set up a classroom that will best support their maths engagement. This involves physical set-up (the classroom itself) as well as emotional and behavioural set-up (behaviours, values, and rules). For example, teachers might talk explicitly about rules and expectations for respectful maths debate, and provide opportunities for all students to talk about maths with their peers, participate in discussions, and record and communicate their ideas.
The key teaching practices discussed in this section are:
|
a) teachers learn about students and their attitudes to maths |
|
B) teachers build a classroom culture that encourages engagement in maths learning |
|
C) teachers organise the classroom environment to encourage engagement in maths learning. |
2) Why is this important?
The way the classroom and class culture are set up matters. Classroom environments can encourage – or discourage – engagement and learning, setting the scene for each maths lesson. This is true both through the physical environment (how the classroom is arranged) and the emotional environment (whether learning about and discussing maths feels safe and inviting). Some of the ways that the physical and emotional environment of maths classrooms make a difference are:
- Attitudes to maths and the way students view themselves as maths students, are a big part of maths learning success (lxxxiii). When teachers purposefully establish a culture where building understanding is valued more than being correct, students are supported to see that not knowing and making mistakes are normal parts of maths learning. This increases their confidence and engagement in maths.
- Working through maths ideas with peers is a highly effective way of building and extending maths understanding (lxxxiv). It’s important that peer discussions are encouraged through as many strategies as possible, including physical prompts like seating arrangements, and non-physical prompts like agreed ways to respectfully debate maths ideas.
- The availability and accessibility of maths tools and representations is a key part of early maths learning (see Practice area 5 for more on this). Students benefit from maths classrooms that have a lot of maths materials for students to see and use (lxxxv).
Negative maths experiences can lead to students thinking they can’t do maths. (Many adults may be able to relate to this, perhaps from their own unpleasant, scary, or boring maths-learning experiences.) It’s important that teachers create a classroom culture where all students feel confident to contribute and listen to ideas,lxxxvi develop and express their ideas, learn from their mistakes, try different maths methods, and problem-solve with and learn from their peers.lxxxvii The way teachers encourage and respond to students, and how classmates engage with one another, is crucial. Good rules and expectations can help with this.
“[An effective maths environment should] maintain clear expectations for learning but allow for flexibility of learning approach, fun, humour, working together, and, in the widest sense, shared responsibility.” - Anderson et. al, 2010lxxxviii
“It’s okay to make mistakes - it’s just your brain growing.” – Student
3) What does good practice look like in real life?
As part of this study, we talked to teachers and school leaders about the strategies that have worked well in their experience. We’ve collected their ideas and strategies here. It is important to reflect carefully about which of these will benefit each school’s unique community and context. No strategies are one-size-fits-all so all these strategies won’t be the right fit for everyone.
The key teacher practices that we focus on are:
- teachers learn about their students and their attitudes to maths
- teachers build a classroom culture that encourages engagement in maths learning
- teachers organise the classroom environment to encourage engagement in maths learning.
a) Teachers learn about their students and their attitudes to maths
The research evidence shows that maths teaching is strengthened when teachers have a trusting relationship with students and know about their lives, interests, and strengths. This enables teachers to pitch maths learning activities and support at the appropriate level, and to use meaningful contexts for maths tasks.
In a maths context, an important part of getting to know students is getting to know their view of themselves as maths students. This is sometimes called their ‘self-concept.’ Students are most motivated when they see maths as manageable and interesting, and view themselves as capable of learning and improving at maths – no matter their current ability level. Teachers can have targeted conversations with students about how they view maths to understand whether students need extra encouragement, extra confidence-building, or extra challenge.
“Sometimes I get the answers and sometimes I don’t. It means I’m learning!” – Student
“I feel great about maths. It’s fun to learn new stuff like fractions.” – Student
Real-life strategies
|
We heard from teachers and school leaders that it works well to… |
|
Invite students to help set up for maths time. We heard that this strategy helps students to feel more ownership of maths activities, and also give students an opportunity to explore and ask about maths materials in a one-on-one context. They then become ‘experts’ in an area and can support their peers to find and use resources. |
|
Bring up maths during casual conversations with students. Talking outside of a maths-learning context helps teachers understand how students are feeling about their maths capabilities, and whether they are in need of extra attention or encouragement. “Building positive relationships with the kid is the key. If they know the teacher cares, then they can do anything!” - Teacher |
|
Draw on students’ current interests to help students feel connected to maths activities. For example, an interest in toy cars is used to help with sorting, grouping, sequencing into patterns, and lining up to compare the number in each group or to make graphs. Teachers describe connecting with students by:
|
b) Teachers build a classroom culture that encourages engagement in maths learning
Negative learning experiences impact on students’ enjoyment and achievement in maths. When maths sessions regularly result in students feeling embarrassed, unable to progress, or overwhelmed, it’s unlikely that they will develop a positive sense of themselves as capable and motivated maths students. Teachers can promote positive maths engagement by establishing ways of working that are encouraging for students. This includes providing opportunities for students to:
- support peers, and be supported by peers, to solve maths problems together
- use respectful language to participate positively in maths discussions and debate
- know which maths tasks encourage being active, loud, or silly with peers
- celebrate mastering new skills
- encounter new and open-ended maths activities that affirm that being unsure and not knowing are normal parts of maths learning
- build perseverance and resilience in maths contexts.
Classroom rules and expectations should support engagement with maths learning. For example, expectations for positive maths debate and discussion can be displayed in the classroom and regularly revisited with students. Teachers might model and encourage students to use phrases with peers that affirm ‘having a go’ or ‘great thinking,’ more than the ‘right answer’. These approaches can provide opportunities for less confident students to talk about their maths ideas, and encourage them to develop perseverance and resilience as they participate.
“[We] build a culture of trying new things and building off each other’s thinking.” – Teacher
“The teacher challenges our brain.” - Student
“I keep trying, even when I’m wrong.” – Student
Real-life strategies
|
We heard from teachers and school leaders that it works well to… |
|
Actively monitor maths group-work dynamics. Teachers observe maths group tasks, with particular attention paid to whether some students are doing more of the work while others are passive. The teacher intervenes to remind the group about agreed practices for maths group-work, for example, ‘Everyone shares ideas.’ |
|
Model how to respond to and debate others’ ideas. Teachers talked to us about how they help students to share and understand their peers’ ideas, learn from each other, see different strategies to solving a problem, and practise mathematical talk. This sort of engagement is supported by overarching class or school ‘norms’ (expectations of behaviour) around respect. Students should also be aware that this is about engaging with the idea rather than the person. Specific strategies modelled and explicitly taught by teachers include:
|
|
Link positive maths behaviours back to familiar school values. In one class, the teacher supports students to value not knowing and making mistakes, with clear messages about how maths discussions should link to the school’s values. “There’s no such thing as ‘I’m the smartest’ – all students start by helping each other. This is all linked to school values like manaakitanga, respect, and care”. (Teacher) |
|
Develop specific practices and guidelines for students to participate in maths discussions and problem solving. Teachers introduce clear expectations about how to participate in maths. These expectations are visible as cards or posters, and teachers regularly remind their students about what positive participation looks like. Guidelines include ways to show respect for others’ ideas, how to justify their ideas, and how to disagree with ideas. The teacher reminds students of these before they begin most maths tasks. Some specific practices for supporting maths talk include:
|
|
Use complex problems to help students get used to the feeling of not knowing. One teacher talked to us about how they give students the opportunity to tackle more complex problems and expand on their ideas, and to explain their thinking to the class. She shared that since doing this, she has noticed that students have become more comfortable with being sometimes right, and sometimes not right. For example, one Year 1 student is given the opportunity to work with a difficult problem, although he usually struggles with sequencing numbers. However, when he is given the opportunity to explain how to solve it up on the board, “Suddenly the lightbulb really went off, while other ‘more able’ kids struggled. If he wasn’t in a classroom like this, then he wouldn’t have had this opportunity.” - Teacher |
|
Occasionally ask questions that have no wrong answers. One teacher spoke to us about the way open activities or questions like ‘What do you notice…?’ invite students’ participation. Ensuring they understand that there are no ‘wrong’ answers (e.g., when making an estimate) means students engage more freely in talking about the maths ideas: “Their idea is valued and they feel special and confident.” |
|
Use self-regulation strategies. Teachers encourage students to self-regulate by:
|
c) Teachers organise the classroom environment to encourage engagement in maths learning
It is well-established that classroom environments provide cues and prompts for students about what learning is valued in the classroom, and how they are expected to interact within it. The physical environment is a powerful tool that teachers can use to stimulate maths learning and engagement. This might involve setting up inviting maths activities, displaying maths concepts and ideas on the walls, or rotating a range of hands-on maths materials and games for students to freely explore. Teachers can also support peer-to-peer learning through purposeful seating arrangements (e.g., mixing stronger maths students with those that need more support), and making rules and expectations visible to all students. This practice also involves how the classroom, furniture, and equipment can be arranged to ensure the inclusion of disabled students.
Real-life strategies
|
We heard from teachers and school leaders that it works well to… |
|
Deliberately match students through seating or grouping. Teachers that we spoke to explained that they closely monitor how well students are collaborating and supporting the maths learning of their buddies, and alter how groups are organised in response. When they notice that a student is struggling, teachers assess whether the environment and learning plan are meeting their needs, considering whether they need extra support or to be partnered with a new buddy. |
|
Rotate maths materials and equipment to invite students’ interest. Changing materials over regularly, and changing their position in the classroom, keeps maths areas looking interesting. Introducing natural materials (stones, shells etc.) and high interest objects and toys from students’ environments is also useful. |
|
Use photos and wall displays to celebrate students’ previous maths work. In one Year 1 class, students look at a displayed photo of one of their classmates next to their arrangement of toy cars stacked into interesting patterns. They point out and discuss the patterns their classmate created. |
|
Include maths-focused and maths-related books on bookshelves and displays. Classroom book displays prominently feature stories involving measurement, counting, addition and subtraction, and searching for largest, smallest, widest, etc. objects or animals. For example – large picture books, specifically books which involve maths concepts, which can be shared. One example is One Hundred Hungry Ants (by Elinor J. Princzes),lxxxix which includes pictures of a hundred ants marching in different arrays as they try to pick up some speed to reach a picnic. (See https://nzmaths.co.nz/picture-books-mathematical-content for more examples of maths picture books.) |
|
Use kidney-shaped or whiteboard-topped desks for maths activities. These are useful for students and teachers to have easy access to materials to demonstrate or use, and be able to see and hear each other’s ideas as they draw, write, or talk. |
4) Good practice example
In a Year 1 class, the teacher uses a range of strategies to encourage students to participate and work with others productively during maths time. Part of this is regularly providing opportunities for students to ask questions, make connections, and be creative.
The teacher regularly talks to her students about a set of cards which contain ideas for working together, tackling a problem, or sharing ideas. Although the students have been at school for less than a year, they are familiar with the protocols, and sometimes refer to them as they work on maths activities.
The teacher supports and models the ideas on the cards as she works with a small group on the mat. She begins by sharing a range of objects from her home environment, talking about her home and her own experiences, to provide a meaningful context for the problem. She invites the students to engage in a complex task – developing different categories for organising: “How do we sort these objects into groups to keep it tidy?” She connects to last week’s task, asking, “What do I mean by sorting into groups? Turn and talk about what you think that means.”
She sorts the students into pairs and gives each pair a group of objects to sort: for example, CDs, food cans, magazines. Students work in pairs and each pair groups them in a range of ways, for example, circular objects, food-related objects. They share what they did to the larger group. The teacher uses questions to prompt them to a deeper level of thinking. She asks: “Can you add to that? Can you explain how you grouped them? Let’s see if this group did it differently. Can I pause you…” She provides vocabulary as students talk about their categories (e.g., cylinder, square, rectangle, category). Each pair then records how many of each there are on their paper, using tally marks.
As each group shares their method, the teacher checks that the others understand before moving on. She then lays out the objects in shape categories, forming a graph, and asks: “How am I organising these? I wonder if anyone notices anything about these squares? Do we agree that they are all squares? How many are there in this group? Can we help him count?”
This activity results in some in-depth discussion about the difference between objects. A student asks how one object was a cylinder and not a circle. The teacher asks the group: “He said these are circles – who agrees? One student responds: “I disagree – because that’s a cylinder!” This idea is supported by other students: “But it’s a circle, at the top!” and “It’s the same, it’s just bigger!” and “But a circle is flat!” The teacher picks up on ideas from the students to deepen the conversation further. “Emily said something really interesting…”
Wall displays that support students’ participation in maths
In several classes ERO observed the use of posters or laminated cards to help students engage in maths tasks or work in groups. Below are some examples from classrooms we visited.
Ideas for talk
“Let’s read the question again”
“Can you explain that part to me? I’m still not sure. Can you explain it in a different way?”
“I have an idea – Do you have any ideas?”
“What materials could we use?”
“How can we check our answer?”
“What are you doing? Why are you doing that?”
“I’m stuck! Do you have any ideas what we can do next?”
Check you both understand
“What parts are you still not sure about?”
“Can you tell me about this?”
“What did we do…First? Next? Then? Last?”
“Let’s practise what we will say when we share”
Talk Moves
Revoicing – “So you’re saying that _________, Do I have that right?”
Repeating – “Can you restate or rephrase what __________ said?”
Reasoning – “Do you agree or disagree? Why”?
Adding on – “Would someone like to add to that?”
Waiting – “Take your time, we’ll wait”
Ideas for Share
- Share your ideas
- Share the pencil
- Share the equipment
- Share the workload
- Take turns
5) Reflective questions for teachers
- How does my maths classroom provide a safe environment for students to share and exchange thinking and ideas?
- How do I respond to students’ incorrect responses?
- How do I support students to enjoy and engage in maths, even when they are not sure of the ‘right’ answer?
- What are my own attitudes to maths? How do I model positive engagement with maths?
- How do I ensure maths tasks are accessible to all my students and they are able to participate meaningfully?
This practice area is about teachers setting up the classroom to encourage students’ maths thinking and maths participation.
When this is going well, the classroom is visibly rich in maths content and materials. Teachers organise the class and classroom in ways that help students to engage with maths tasks and work collaboratively. Classroom rules and expectations support students to share ideas, ask questions, and participate in mathematical discussion and debate.
In this section, we describe why the classroom learning environment is important for encouraging mathematical thinking. We also offer practical guidance on how teachers can grow this practice within their own class.
Overview of this section
This part of the report sets out useful information about how teachers can set up their learning environment so that its supports mathematical thinking and enjoyment of maths. It includes:
- What is this practice area?
- Why is this important?
- What does good practice look like in real life?
- Good practice example
- Reflective questions for teachers
1) What is this practice area?
This practice area is about teachers understanding their students well, and taking action to set up a classroom that will best support their maths engagement. This involves physical set-up (the classroom itself) as well as emotional and behavioural set-up (behaviours, values, and rules). For example, teachers might talk explicitly about rules and expectations for respectful maths debate, and provide opportunities for all students to talk about maths with their peers, participate in discussions, and record and communicate their ideas.
The key teaching practices discussed in this section are:
|
a) teachers learn about students and their attitudes to maths |
|
B) teachers build a classroom culture that encourages engagement in maths learning |
|
C) teachers organise the classroom environment to encourage engagement in maths learning. |
2) Why is this important?
The way the classroom and class culture are set up matters. Classroom environments can encourage – or discourage – engagement and learning, setting the scene for each maths lesson. This is true both through the physical environment (how the classroom is arranged) and the emotional environment (whether learning about and discussing maths feels safe and inviting). Some of the ways that the physical and emotional environment of maths classrooms make a difference are:
- Attitudes to maths and the way students view themselves as maths students, are a big part of maths learning success (lxxxiii). When teachers purposefully establish a culture where building understanding is valued more than being correct, students are supported to see that not knowing and making mistakes are normal parts of maths learning. This increases their confidence and engagement in maths.
- Working through maths ideas with peers is a highly effective way of building and extending maths understanding (lxxxiv). It’s important that peer discussions are encouraged through as many strategies as possible, including physical prompts like seating arrangements, and non-physical prompts like agreed ways to respectfully debate maths ideas.
- The availability and accessibility of maths tools and representations is a key part of early maths learning (see Practice area 5 for more on this). Students benefit from maths classrooms that have a lot of maths materials for students to see and use (lxxxv).
Negative maths experiences can lead to students thinking they can’t do maths. (Many adults may be able to relate to this, perhaps from their own unpleasant, scary, or boring maths-learning experiences.) It’s important that teachers create a classroom culture where all students feel confident to contribute and listen to ideas,lxxxvi develop and express their ideas, learn from their mistakes, try different maths methods, and problem-solve with and learn from their peers.lxxxvii The way teachers encourage and respond to students, and how classmates engage with one another, is crucial. Good rules and expectations can help with this.
“[An effective maths environment should] maintain clear expectations for learning but allow for flexibility of learning approach, fun, humour, working together, and, in the widest sense, shared responsibility.” - Anderson et. al, 2010lxxxviii
“It’s okay to make mistakes - it’s just your brain growing.” – Student
3) What does good practice look like in real life?
As part of this study, we talked to teachers and school leaders about the strategies that have worked well in their experience. We’ve collected their ideas and strategies here. It is important to reflect carefully about which of these will benefit each school’s unique community and context. No strategies are one-size-fits-all so all these strategies won’t be the right fit for everyone.
The key teacher practices that we focus on are:
- teachers learn about their students and their attitudes to maths
- teachers build a classroom culture that encourages engagement in maths learning
- teachers organise the classroom environment to encourage engagement in maths learning.
a) Teachers learn about their students and their attitudes to maths
The research evidence shows that maths teaching is strengthened when teachers have a trusting relationship with students and know about their lives, interests, and strengths. This enables teachers to pitch maths learning activities and support at the appropriate level, and to use meaningful contexts for maths tasks.
In a maths context, an important part of getting to know students is getting to know their view of themselves as maths students. This is sometimes called their ‘self-concept.’ Students are most motivated when they see maths as manageable and interesting, and view themselves as capable of learning and improving at maths – no matter their current ability level. Teachers can have targeted conversations with students about how they view maths to understand whether students need extra encouragement, extra confidence-building, or extra challenge.
“Sometimes I get the answers and sometimes I don’t. It means I’m learning!” – Student
“I feel great about maths. It’s fun to learn new stuff like fractions.” – Student
Real-life strategies
|
We heard from teachers and school leaders that it works well to… |
|
Invite students to help set up for maths time. We heard that this strategy helps students to feel more ownership of maths activities, and also give students an opportunity to explore and ask about maths materials in a one-on-one context. They then become ‘experts’ in an area and can support their peers to find and use resources. |
|
Bring up maths during casual conversations with students. Talking outside of a maths-learning context helps teachers understand how students are feeling about their maths capabilities, and whether they are in need of extra attention or encouragement. “Building positive relationships with the kid is the key. If they know the teacher cares, then they can do anything!” - Teacher |
|
Draw on students’ current interests to help students feel connected to maths activities. For example, an interest in toy cars is used to help with sorting, grouping, sequencing into patterns, and lining up to compare the number in each group or to make graphs. Teachers describe connecting with students by:
|
b) Teachers build a classroom culture that encourages engagement in maths learning
Negative learning experiences impact on students’ enjoyment and achievement in maths. When maths sessions regularly result in students feeling embarrassed, unable to progress, or overwhelmed, it’s unlikely that they will develop a positive sense of themselves as capable and motivated maths students. Teachers can promote positive maths engagement by establishing ways of working that are encouraging for students. This includes providing opportunities for students to:
- support peers, and be supported by peers, to solve maths problems together
- use respectful language to participate positively in maths discussions and debate
- know which maths tasks encourage being active, loud, or silly with peers
- celebrate mastering new skills
- encounter new and open-ended maths activities that affirm that being unsure and not knowing are normal parts of maths learning
- build perseverance and resilience in maths contexts.
Classroom rules and expectations should support engagement with maths learning. For example, expectations for positive maths debate and discussion can be displayed in the classroom and regularly revisited with students. Teachers might model and encourage students to use phrases with peers that affirm ‘having a go’ or ‘great thinking,’ more than the ‘right answer’. These approaches can provide opportunities for less confident students to talk about their maths ideas, and encourage them to develop perseverance and resilience as they participate.
“[We] build a culture of trying new things and building off each other’s thinking.” – Teacher
“The teacher challenges our brain.” - Student
“I keep trying, even when I’m wrong.” – Student
Real-life strategies
|
We heard from teachers and school leaders that it works well to… |
|
Actively monitor maths group-work dynamics. Teachers observe maths group tasks, with particular attention paid to whether some students are doing more of the work while others are passive. The teacher intervenes to remind the group about agreed practices for maths group-work, for example, ‘Everyone shares ideas.’ |
|
Model how to respond to and debate others’ ideas. Teachers talked to us about how they help students to share and understand their peers’ ideas, learn from each other, see different strategies to solving a problem, and practise mathematical talk. This sort of engagement is supported by overarching class or school ‘norms’ (expectations of behaviour) around respect. Students should also be aware that this is about engaging with the idea rather than the person. Specific strategies modelled and explicitly taught by teachers include:
|
|
Link positive maths behaviours back to familiar school values. In one class, the teacher supports students to value not knowing and making mistakes, with clear messages about how maths discussions should link to the school’s values. “There’s no such thing as ‘I’m the smartest’ – all students start by helping each other. This is all linked to school values like manaakitanga, respect, and care”. (Teacher) |
|
Develop specific practices and guidelines for students to participate in maths discussions and problem solving. Teachers introduce clear expectations about how to participate in maths. These expectations are visible as cards or posters, and teachers regularly remind their students about what positive participation looks like. Guidelines include ways to show respect for others’ ideas, how to justify their ideas, and how to disagree with ideas. The teacher reminds students of these before they begin most maths tasks. Some specific practices for supporting maths talk include:
|
|
Use complex problems to help students get used to the feeling of not knowing. One teacher talked to us about how they give students the opportunity to tackle more complex problems and expand on their ideas, and to explain their thinking to the class. She shared that since doing this, she has noticed that students have become more comfortable with being sometimes right, and sometimes not right. For example, one Year 1 student is given the opportunity to work with a difficult problem, although he usually struggles with sequencing numbers. However, when he is given the opportunity to explain how to solve it up on the board, “Suddenly the lightbulb really went off, while other ‘more able’ kids struggled. If he wasn’t in a classroom like this, then he wouldn’t have had this opportunity.” - Teacher |
|
Occasionally ask questions that have no wrong answers. One teacher spoke to us about the way open activities or questions like ‘What do you notice…?’ invite students’ participation. Ensuring they understand that there are no ‘wrong’ answers (e.g., when making an estimate) means students engage more freely in talking about the maths ideas: “Their idea is valued and they feel special and confident.” |
|
Use self-regulation strategies. Teachers encourage students to self-regulate by:
|
c) Teachers organise the classroom environment to encourage engagement in maths learning
It is well-established that classroom environments provide cues and prompts for students about what learning is valued in the classroom, and how they are expected to interact within it. The physical environment is a powerful tool that teachers can use to stimulate maths learning and engagement. This might involve setting up inviting maths activities, displaying maths concepts and ideas on the walls, or rotating a range of hands-on maths materials and games for students to freely explore. Teachers can also support peer-to-peer learning through purposeful seating arrangements (e.g., mixing stronger maths students with those that need more support), and making rules and expectations visible to all students. This practice also involves how the classroom, furniture, and equipment can be arranged to ensure the inclusion of disabled students.
Real-life strategies
|
We heard from teachers and school leaders that it works well to… |
|
Deliberately match students through seating or grouping. Teachers that we spoke to explained that they closely monitor how well students are collaborating and supporting the maths learning of their buddies, and alter how groups are organised in response. When they notice that a student is struggling, teachers assess whether the environment and learning plan are meeting their needs, considering whether they need extra support or to be partnered with a new buddy. |
|
Rotate maths materials and equipment to invite students’ interest. Changing materials over regularly, and changing their position in the classroom, keeps maths areas looking interesting. Introducing natural materials (stones, shells etc.) and high interest objects and toys from students’ environments is also useful. |
|
Use photos and wall displays to celebrate students’ previous maths work. In one Year 1 class, students look at a displayed photo of one of their classmates next to their arrangement of toy cars stacked into interesting patterns. They point out and discuss the patterns their classmate created. |
|
Include maths-focused and maths-related books on bookshelves and displays. Classroom book displays prominently feature stories involving measurement, counting, addition and subtraction, and searching for largest, smallest, widest, etc. objects or animals. For example – large picture books, specifically books which involve maths concepts, which can be shared. One example is One Hundred Hungry Ants (by Elinor J. Princzes),lxxxix which includes pictures of a hundred ants marching in different arrays as they try to pick up some speed to reach a picnic. (See https://nzmaths.co.nz/picture-books-mathematical-content for more examples of maths picture books.) |
|
Use kidney-shaped or whiteboard-topped desks for maths activities. These are useful for students and teachers to have easy access to materials to demonstrate or use, and be able to see and hear each other’s ideas as they draw, write, or talk. |
4) Good practice example
In a Year 1 class, the teacher uses a range of strategies to encourage students to participate and work with others productively during maths time. Part of this is regularly providing opportunities for students to ask questions, make connections, and be creative.
The teacher regularly talks to her students about a set of cards which contain ideas for working together, tackling a problem, or sharing ideas. Although the students have been at school for less than a year, they are familiar with the protocols, and sometimes refer to them as they work on maths activities.
The teacher supports and models the ideas on the cards as she works with a small group on the mat. She begins by sharing a range of objects from her home environment, talking about her home and her own experiences, to provide a meaningful context for the problem. She invites the students to engage in a complex task – developing different categories for organising: “How do we sort these objects into groups to keep it tidy?” She connects to last week’s task, asking, “What do I mean by sorting into groups? Turn and talk about what you think that means.”
She sorts the students into pairs and gives each pair a group of objects to sort: for example, CDs, food cans, magazines. Students work in pairs and each pair groups them in a range of ways, for example, circular objects, food-related objects. They share what they did to the larger group. The teacher uses questions to prompt them to a deeper level of thinking. She asks: “Can you add to that? Can you explain how you grouped them? Let’s see if this group did it differently. Can I pause you…” She provides vocabulary as students talk about their categories (e.g., cylinder, square, rectangle, category). Each pair then records how many of each there are on their paper, using tally marks.
As each group shares their method, the teacher checks that the others understand before moving on. She then lays out the objects in shape categories, forming a graph, and asks: “How am I organising these? I wonder if anyone notices anything about these squares? Do we agree that they are all squares? How many are there in this group? Can we help him count?”
This activity results in some in-depth discussion about the difference between objects. A student asks how one object was a cylinder and not a circle. The teacher asks the group: “He said these are circles – who agrees? One student responds: “I disagree – because that’s a cylinder!” This idea is supported by other students: “But it’s a circle, at the top!” and “It’s the same, it’s just bigger!” and “But a circle is flat!” The teacher picks up on ideas from the students to deepen the conversation further. “Emily said something really interesting…”
Wall displays that support students’ participation in maths
In several classes ERO observed the use of posters or laminated cards to help students engage in maths tasks or work in groups. Below are some examples from classrooms we visited.
Ideas for talk
“Let’s read the question again”
“Can you explain that part to me? I’m still not sure. Can you explain it in a different way?”
“I have an idea – Do you have any ideas?”
“What materials could we use?”
“How can we check our answer?”
“What are you doing? Why are you doing that?”
“I’m stuck! Do you have any ideas what we can do next?”
Check you both understand
“What parts are you still not sure about?”
“Can you tell me about this?”
“What did we do…First? Next? Then? Last?”
“Let’s practise what we will say when we share”
Talk Moves
Revoicing – “So you’re saying that _________, Do I have that right?”
Repeating – “Can you restate or rephrase what __________ said?”
Reasoning – “Do you agree or disagree? Why”?
Adding on – “Would someone like to add to that?”
Waiting – “Take your time, we’ll wait”
Ideas for Share
- Share your ideas
- Share the pencil
- Share the equipment
- Share the workload
- Take turns
5) Reflective questions for teachers
- How does my maths classroom provide a safe environment for students to share and exchange thinking and ideas?
- How do I respond to students’ incorrect responses?
- How do I support students to enjoy and engage in maths, even when they are not sure of the ‘right’ answer?
- What are my own attitudes to maths? How do I model positive engagement with maths?
- How do I ensure maths tasks are accessible to all my students and they are able to participate meaningfully?
Practice area 7: Teachers make the most of moments throughout the day to highlight and use maths
This practice area is about teachers planning for and seizing opportunities to bring maths talk into everyday school life.
When this is going well, teachers find ways to mix mathematical ideas into class activities throughout the day, not only during dedicated maths learning times. This means students can encounter maths ideas and apply their maths skills and knowledge in a variety of contexts, like routines, play, and within other curriculum areas.
In this section, we set out why it is important for teachers to make the most of moments throughout the day to highlight and use mathematics. We offer practical guidance on how teachers can put this into practice in their own classrooms.
Overview of this section
This part of the report sets out useful information about how teachers make the most of moments throughout the day to highlight and use mathematics. It includes:
- What is this practice area?
- Why is this important?
- What does good practice look like in real life?
- Good practice example
- Reflective questions for teachers
”Opportunities for learning mathematics typically arise out of children’s everyday activities: counting, playing with mathematical shapes, telling time, estimating distance, sharing, cooking, and playing games.” – Anthony & Walshaw, 2007(xc)
1) What is this practice area?
This practice area is about teachers strengthening students’ understandings of maths by highlighting all the ways that maths ideas are relevant within the students’ world. This can occur in planned or spontaneous ways, within the range of everyday activities that take place in a school day, including routines, play, and other curriculum areas. Teachers can add value and complexity to all sorts of contexts by providing questions or prompts, encouraging problem-solving, and reinforcing mathematical vocabulary.xci
The key teaching practices discussed in this section are:
|
a) teachers plan how maths ideas are incorporated into a range of activities |
|
b) teachers make links to maths when teaching other curriculum areas |
|
c) teachers find spontaneous ways to bring maths concepts into play and routine tasks. |
2) Why is this important?
Regularly highlighting maths concepts in contexts that aren’t maths sessions is a powerful teaching tool. It helps students to see the ‘hidden maths’ that is all around, which can ignite their interest, curiosity, and engagement in maths learning.
When maths keeps popping up in everyday activities, like routines and other subject areas, students are able to see the relevance and application of maths throughout their lives. Students make connections between maths ideas and their own experiences, strengthening their understanding.xcii This practice also provides additional, meaningful opportunities to practise maths skills.
“The most effective settings for young students provide a balance between opportunities for children to benefit from teacher-initiated group work and freely chosen, yet potentially instructive, play activities.” – Anthony & Walshaw, 2007(xciii)
Games and play as maths contexts
It is well-established that meaningful learning happens in young children’s playxciv and that play can support the development of mathematical ideas. Well-chosen play activities and games help to maintain maths skills and knowledge, introduce complex ideas, and promote the idea that maths can be fun. Games “can be an engaging way to practise and extend skills… build on children’s mathematics knowledge, generate repeated practice in a motivating context, and give children and practitioners an opportunity to discuss strategies and ideas.”xcv
3) What does good practice look like in real life?
As part of this study, we talked to teachers and school leaders about the strategies that have worked well in their experience. We’ve collected their ideas and strategies here. It is important to reflect carefully about which of these will benefit each school’s unique community and context. No strategies are one-size-fits-all so all these strategies won’t be the right fit for everyone.
The key teacher practices that we focus on are:
- teachers plan how maths ideas are incorporated into a range of activities
- teachers make links to maths learning when teaching other curriculum areas
- teachers find spontaneous ways to bring maths concepts into play and routine tasks.
a) Teachers plan how maths ideas are incorporated into a range of activities
With careful planning, teachers can deliberately weave current or prior maths learning into other school activities. Year 1-3 classroom activities are full of opportunities for highlighting maths ideas, including beginning of the day activities (counting how many students are present, tallying or graphing modes of travel to school, colours worn, etc.) and shared reading of picture books where teachers can surface maths ideas. Taking an intentional, planned approach to revisiting maths in small ways throughout the day ensures that students have plenty of exposure to maths ideas.
Real-life strategies
|
We heard from teachers and school leaders that it works well to… |
|
Schedule regular fun-based activities which include maths components. These activities may not be intended specifically for maths learning, but may include a maths component so students do maths without realising it. Teachers spoke to us about how they weave in maths ideas when they are talking about timetabling or time. Dividing the class into groups for physical activities and playing games provide fertile contexts for highlighting maths. For example:
In one school, teachers recognise the mathematical aspects embedded in actions included in physical education or perception motor programme (PMP) activities. For example, students walking around a shape blindfolded, or balancing on the shape, and then telling the teacher what shape it was. Students encounter directional language in their activities: for example, moving a wobble board left/right and forwards/backwards, and running in different compass directions. |
|
Link maths to current events and celebrations. In one school, during NZ bird week, they predict and then undertake observations where they count birds in their school and make a tally chart. This is undertaken annually, and the class compares results with previous years. This activity links to skills of estimation and counting and builds students’ understanding of aspects of statistics. Prior to ANZAC day, a Year 1-2 class cooked ANZAC biscuits for maths. This activity incorporated ideas of capacity and involved every student in measuring. |
|
Bring maths into integrated ‘theme’ or ‘topic’ activities. In one Year 2-3 class, a teacher uses a recent interest in baking, prompted from a recent school activity and a television show, to illustrate multiplication. In a warm-up activity, she shares photos of muffins arranged in trays. The students work in pairs to find how many muffins there are all together. They then move to tables where they populate real muffin trays with cut out muffins, and then record their findings as diagrams, word sentences, and multiplication equations. |
|
Use milestones which include a mathematical component. This may be something structured and planned like ‘the first 100 days of school’, which ERO observed in a New Entrant classroom (see the box below), or smaller-scale. One teacher uses a calendar to count how many days are left in a month or week. Students count days together, and are prompted to think mathematically by answering questions like:
|
Short story: The first 100 days of school
In one New Entrant classroom, part of their daily routine is an activity where the class reviews their progress towards 100 days at school. The class looks forward to a special celebration on the hundredth day. They begin by counting from 1 until they reach the next day after their previous count. The characteristics of the new number are then explored, with purposeful prompting questions from the teacher:
- What was yesterday’s number?
- What will tomorrow’s be?
- Can someone find it for me on the hundreds chart?
- Can someone show me the number with the bundles of 10?
- If today is the 72nd day of school, how many days until the 100th day?
- How did you figure that out?
b) Teachers make links to maths learning when teaching other curriculum areas
Incorporating maths ideas into other curriculum areas like science, social studies, writing, and the arts helps students practice and make sense of maths concepts.
It’s useful to take a deliberate, planned approach to maximising the possibilities embedded within the associated curriculum area. Taking time to explore these possibilities before teaching means that teachers can purposefully make the links to maths ideas in ways that are clear to students. Students can then make meaningful links to their knowledge and prior learning. This is an effective way to keep students practising and seeing maths throughout the day.
“Maths links to everything, like science.” – Student
“I believe in integrating maths into your other areas, because that’s something that is really crucial. That kids see it as having value when it’s not necessarily in the lead, it’s not maths time.” – Teacher
“We look at real-life context, for integrated opportunities, literacy and maths.” - Teacher
Real-life strategies
|
We heard from teachers and school leaders that it works well to… |
|
Integrate maths concepts with physical education (PE). This is a particularly effective context for linking to maths, as it offers whole-body contexts for making abstract maths concepts feel physically ‘real’ to students. At one school during a P.E. lesson, numbers are put under spaced-out cones on the school field. Students have to find the biggest numbers they can, and then get into a line from smallest to biggest. Another example is during cross-country training, where students receive a bean for every lap they run. After the training they come back to class and create a bar on a class graph to show their number of laps. |
|
Be alert to opportunities to spontaneously blend maths talk into other learning areas. A teacher observes Year 1 students making colour patterns during arts and craft. She draws alongside one student and describes the pattern she is making. She talks about the pattern as a sequence and asks the student to guess what is next in the pattern. She uses algebraic symbols to talk about the pattern. She also clarifies the mathematical content of the conversation, affirming, “That is very clever maths!” |
|
Take a flexible approach in response to questions and ideas from students, to make the most of opportunities that emerge. For example, at the start of a maths lesson in one new entrant class, one student, unprompted, asks if they can count together. The teacher seizes the opportunity, grabs the abacus and uses it to skip-count in 5s, stopping at different times to show how many 5s in a number (e.g., stopping at 30 – how many 5s have we counted so far? That’s right, there are six 5s in 30!). |
|
Work with colleagues to brainstorm the maths opportunities within different topics. Two teachers that we spoke to regularly work together on science and maths integration units, drawing on each other’s strengths, interests, and ideas. (See the ‘Good practice example’ later in this section for more on this.) |
c) Teachers find spontaneous ways to bring maths concepts into play and routine tasks
Teachers can make the most of daily routines and play activities to highlight and use maths. This means being alert to the maths concepts or vocabulary that might emerge as students engage in routines and play, and being ready to prompt students to extend their thinking or make connections.
For example, students playing board games with evenly spaced number sequences have opportunities to learn about or practise counting forwards and backwards, patterns, addition and subtraction, or place value ideas. Sorting groups of objects is an important way to encounter mathematical concepts such as geometry (identifying characteristics of shapes), statistics (organising into groups and making comparisons), and algebra (making sequences and repeated patterns).
“Children become familiar with concepts without realising it’s maths… Kids say ‘I can’t do maths’, and I always say, ‘Of course you can do maths! You’ve turned up at school and you know what day of the week it is!’” - Teacher
“What red hands you have! How many red fingers are there? Show me.” - Teacher
Real-life strategies
|
We heard from teachers and school leaders that it works well to… |
|
Use routines as opportunities to count or talk about sequences and patterns. This includes activities like:
|
|
Use counting and countdowns when students move between activities. For example, students quickly getting to the mat before a countdown ends. |
|
Consider possible maths links when setting up play equipment. A rural school we visited told us how during summertime, students playing in a water trough are encouraged to figure out how much water they could fit in the trough using different sized spoons and measuring equipment. |
|
Add maths complexity to art activities. In one classroom we visited, the teacher offers support to a student who is building a clay nest. The teacher asks questions, like: “What colours are you using?” and “How many legs will there be all together?” The teacher then writes an equation on a post-it note: ‘2 + 2 = ?’ |
|
Seize the moment when numbers are mentioned in books. Some reading text refers to one million CDs being sold worldwide. The teacher asks the students to discuss what this means, and then develops these ideas, writing the number and discussing how it relates to other numbers (bigger than, smaller than, the numbers before and after etc.) |
|
Use skip-counting instead of regular counting. We heard how teachers would take every opportunity they could to use skip-counting, for example, when students were lining up outside of class, to help build patterns for multiplication. |
4) Good practice example
Two teachers work together in a Year 2-3 class to purposefully integrate maths with science, enriching the learning in both curriculum areas.
During a discussion, these teachers recognise how maths naturally fits into their planned science topic - examining the solar system. They plan a range of maths-related solar system activities, such as finding out the distances between planets, and recording the distance measurements. Students have been leaning about orbit and rotation cycles, and looking at how many days it takes the earth to orbit the sun. They also discuss aspects of multiplication and proportionality, like how many times the earth can fit into the sun.
Another of these teachers’ science-maths integration units is focused on shadows. Students spend a day measuring and recording the length of their own shadows as the day progresses. Prior to the measuring activity, the class practised measuring different objects accurately, and discussed what they thought might happen – predicting whether the measurements would change and if they would get longer or shorter.
Students work together to measure their shadows every hour (six time points through the day), and mark the changing lengths of their shadows with chalk as well as recording the measurements in notebooks. This activity is used to reinforce the science ideas they are learning about the daily rotation of the earth, as well as building measurement skills. The students complete the activity in groups of three, which provides less confident students with support to undertake the task, and an adult also checks the accuracy of the measurements. The measurements are then collated, analysed in a class discussion, and displayed in a bar graph which they design together. As a class, they talk about why they use a bar graph and how it helps with this subject to express their ideas. The learning activity is then captured in photos and text and displayed on the wall.
5) Reflective questions for teachers
- What opportunities are there in my daily class routines to practise maths skills, develop maths knowledge, or help students make links to mathematical ideas?
- Would it be useful to map out my daily activities and plan for more intentional weaving of maths throughout the day?
- In what ways do I weave maths into other curriculum area learning? How could I do this more often?
- Am I aware of which maths games are available to me, and how they can link to my planned maths learning? What other classroom resources could I use to promote mathematical thinking and skills?
This practice area is about teachers planning for and seizing opportunities to bring maths talk into everyday school life.
When this is going well, teachers find ways to mix mathematical ideas into class activities throughout the day, not only during dedicated maths learning times. This means students can encounter maths ideas and apply their maths skills and knowledge in a variety of contexts, like routines, play, and within other curriculum areas.
In this section, we set out why it is important for teachers to make the most of moments throughout the day to highlight and use mathematics. We offer practical guidance on how teachers can put this into practice in their own classrooms.
Overview of this section
This part of the report sets out useful information about how teachers make the most of moments throughout the day to highlight and use mathematics. It includes:
- What is this practice area?
- Why is this important?
- What does good practice look like in real life?
- Good practice example
- Reflective questions for teachers
”Opportunities for learning mathematics typically arise out of children’s everyday activities: counting, playing with mathematical shapes, telling time, estimating distance, sharing, cooking, and playing games.” – Anthony & Walshaw, 2007(xc)
1) What is this practice area?
This practice area is about teachers strengthening students’ understandings of maths by highlighting all the ways that maths ideas are relevant within the students’ world. This can occur in planned or spontaneous ways, within the range of everyday activities that take place in a school day, including routines, play, and other curriculum areas. Teachers can add value and complexity to all sorts of contexts by providing questions or prompts, encouraging problem-solving, and reinforcing mathematical vocabulary.xci
The key teaching practices discussed in this section are:
|
a) teachers plan how maths ideas are incorporated into a range of activities |
|
b) teachers make links to maths when teaching other curriculum areas |
|
c) teachers find spontaneous ways to bring maths concepts into play and routine tasks. |
2) Why is this important?
Regularly highlighting maths concepts in contexts that aren’t maths sessions is a powerful teaching tool. It helps students to see the ‘hidden maths’ that is all around, which can ignite their interest, curiosity, and engagement in maths learning.
When maths keeps popping up in everyday activities, like routines and other subject areas, students are able to see the relevance and application of maths throughout their lives. Students make connections between maths ideas and their own experiences, strengthening their understanding.xcii This practice also provides additional, meaningful opportunities to practise maths skills.
“The most effective settings for young students provide a balance between opportunities for children to benefit from teacher-initiated group work and freely chosen, yet potentially instructive, play activities.” – Anthony & Walshaw, 2007(xciii)
Games and play as maths contexts
It is well-established that meaningful learning happens in young children’s playxciv and that play can support the development of mathematical ideas. Well-chosen play activities and games help to maintain maths skills and knowledge, introduce complex ideas, and promote the idea that maths can be fun. Games “can be an engaging way to practise and extend skills… build on children’s mathematics knowledge, generate repeated practice in a motivating context, and give children and practitioners an opportunity to discuss strategies and ideas.”xcv
3) What does good practice look like in real life?
As part of this study, we talked to teachers and school leaders about the strategies that have worked well in their experience. We’ve collected their ideas and strategies here. It is important to reflect carefully about which of these will benefit each school’s unique community and context. No strategies are one-size-fits-all so all these strategies won’t be the right fit for everyone.
The key teacher practices that we focus on are:
- teachers plan how maths ideas are incorporated into a range of activities
- teachers make links to maths learning when teaching other curriculum areas
- teachers find spontaneous ways to bring maths concepts into play and routine tasks.
a) Teachers plan how maths ideas are incorporated into a range of activities
With careful planning, teachers can deliberately weave current or prior maths learning into other school activities. Year 1-3 classroom activities are full of opportunities for highlighting maths ideas, including beginning of the day activities (counting how many students are present, tallying or graphing modes of travel to school, colours worn, etc.) and shared reading of picture books where teachers can surface maths ideas. Taking an intentional, planned approach to revisiting maths in small ways throughout the day ensures that students have plenty of exposure to maths ideas.
Real-life strategies
|
We heard from teachers and school leaders that it works well to… |
|
Schedule regular fun-based activities which include maths components. These activities may not be intended specifically for maths learning, but may include a maths component so students do maths without realising it. Teachers spoke to us about how they weave in maths ideas when they are talking about timetabling or time. Dividing the class into groups for physical activities and playing games provide fertile contexts for highlighting maths. For example:
In one school, teachers recognise the mathematical aspects embedded in actions included in physical education or perception motor programme (PMP) activities. For example, students walking around a shape blindfolded, or balancing on the shape, and then telling the teacher what shape it was. Students encounter directional language in their activities: for example, moving a wobble board left/right and forwards/backwards, and running in different compass directions. |
|
Link maths to current events and celebrations. In one school, during NZ bird week, they predict and then undertake observations where they count birds in their school and make a tally chart. This is undertaken annually, and the class compares results with previous years. This activity links to skills of estimation and counting and builds students’ understanding of aspects of statistics. Prior to ANZAC day, a Year 1-2 class cooked ANZAC biscuits for maths. This activity incorporated ideas of capacity and involved every student in measuring. |
|
Bring maths into integrated ‘theme’ or ‘topic’ activities. In one Year 2-3 class, a teacher uses a recent interest in baking, prompted from a recent school activity and a television show, to illustrate multiplication. In a warm-up activity, she shares photos of muffins arranged in trays. The students work in pairs to find how many muffins there are all together. They then move to tables where they populate real muffin trays with cut out muffins, and then record their findings as diagrams, word sentences, and multiplication equations. |
|
Use milestones which include a mathematical component. This may be something structured and planned like ‘the first 100 days of school’, which ERO observed in a New Entrant classroom (see the box below), or smaller-scale. One teacher uses a calendar to count how many days are left in a month or week. Students count days together, and are prompted to think mathematically by answering questions like:
|
Short story: The first 100 days of school
In one New Entrant classroom, part of their daily routine is an activity where the class reviews their progress towards 100 days at school. The class looks forward to a special celebration on the hundredth day. They begin by counting from 1 until they reach the next day after their previous count. The characteristics of the new number are then explored, with purposeful prompting questions from the teacher:
- What was yesterday’s number?
- What will tomorrow’s be?
- Can someone find it for me on the hundreds chart?
- Can someone show me the number with the bundles of 10?
- If today is the 72nd day of school, how many days until the 100th day?
- How did you figure that out?
b) Teachers make links to maths learning when teaching other curriculum areas
Incorporating maths ideas into other curriculum areas like science, social studies, writing, and the arts helps students practice and make sense of maths concepts.
It’s useful to take a deliberate, planned approach to maximising the possibilities embedded within the associated curriculum area. Taking time to explore these possibilities before teaching means that teachers can purposefully make the links to maths ideas in ways that are clear to students. Students can then make meaningful links to their knowledge and prior learning. This is an effective way to keep students practising and seeing maths throughout the day.
“Maths links to everything, like science.” – Student
“I believe in integrating maths into your other areas, because that’s something that is really crucial. That kids see it as having value when it’s not necessarily in the lead, it’s not maths time.” – Teacher
“We look at real-life context, for integrated opportunities, literacy and maths.” - Teacher
Real-life strategies
|
We heard from teachers and school leaders that it works well to… |
|
Integrate maths concepts with physical education (PE). This is a particularly effective context for linking to maths, as it offers whole-body contexts for making abstract maths concepts feel physically ‘real’ to students. At one school during a P.E. lesson, numbers are put under spaced-out cones on the school field. Students have to find the biggest numbers they can, and then get into a line from smallest to biggest. Another example is during cross-country training, where students receive a bean for every lap they run. After the training they come back to class and create a bar on a class graph to show their number of laps. |
|
Be alert to opportunities to spontaneously blend maths talk into other learning areas. A teacher observes Year 1 students making colour patterns during arts and craft. She draws alongside one student and describes the pattern she is making. She talks about the pattern as a sequence and asks the student to guess what is next in the pattern. She uses algebraic symbols to talk about the pattern. She also clarifies the mathematical content of the conversation, affirming, “That is very clever maths!” |
|
Take a flexible approach in response to questions and ideas from students, to make the most of opportunities that emerge. For example, at the start of a maths lesson in one new entrant class, one student, unprompted, asks if they can count together. The teacher seizes the opportunity, grabs the abacus and uses it to skip-count in 5s, stopping at different times to show how many 5s in a number (e.g., stopping at 30 – how many 5s have we counted so far? That’s right, there are six 5s in 30!). |
|
Work with colleagues to brainstorm the maths opportunities within different topics. Two teachers that we spoke to regularly work together on science and maths integration units, drawing on each other’s strengths, interests, and ideas. (See the ‘Good practice example’ later in this section for more on this.) |
c) Teachers find spontaneous ways to bring maths concepts into play and routine tasks
Teachers can make the most of daily routines and play activities to highlight and use maths. This means being alert to the maths concepts or vocabulary that might emerge as students engage in routines and play, and being ready to prompt students to extend their thinking or make connections.
For example, students playing board games with evenly spaced number sequences have opportunities to learn about or practise counting forwards and backwards, patterns, addition and subtraction, or place value ideas. Sorting groups of objects is an important way to encounter mathematical concepts such as geometry (identifying characteristics of shapes), statistics (organising into groups and making comparisons), and algebra (making sequences and repeated patterns).
“Children become familiar with concepts without realising it’s maths… Kids say ‘I can’t do maths’, and I always say, ‘Of course you can do maths! You’ve turned up at school and you know what day of the week it is!’” - Teacher
“What red hands you have! How many red fingers are there? Show me.” - Teacher
Real-life strategies
|
We heard from teachers and school leaders that it works well to… |
|
Use routines as opportunities to count or talk about sequences and patterns. This includes activities like:
|
|
Use counting and countdowns when students move between activities. For example, students quickly getting to the mat before a countdown ends. |
|
Consider possible maths links when setting up play equipment. A rural school we visited told us how during summertime, students playing in a water trough are encouraged to figure out how much water they could fit in the trough using different sized spoons and measuring equipment. |
|
Add maths complexity to art activities. In one classroom we visited, the teacher offers support to a student who is building a clay nest. The teacher asks questions, like: “What colours are you using?” and “How many legs will there be all together?” The teacher then writes an equation on a post-it note: ‘2 + 2 = ?’ |
|
Seize the moment when numbers are mentioned in books. Some reading text refers to one million CDs being sold worldwide. The teacher asks the students to discuss what this means, and then develops these ideas, writing the number and discussing how it relates to other numbers (bigger than, smaller than, the numbers before and after etc.) |
|
Use skip-counting instead of regular counting. We heard how teachers would take every opportunity they could to use skip-counting, for example, when students were lining up outside of class, to help build patterns for multiplication. |
4) Good practice example
Two teachers work together in a Year 2-3 class to purposefully integrate maths with science, enriching the learning in both curriculum areas.
During a discussion, these teachers recognise how maths naturally fits into their planned science topic - examining the solar system. They plan a range of maths-related solar system activities, such as finding out the distances between planets, and recording the distance measurements. Students have been leaning about orbit and rotation cycles, and looking at how many days it takes the earth to orbit the sun. They also discuss aspects of multiplication and proportionality, like how many times the earth can fit into the sun.
Another of these teachers’ science-maths integration units is focused on shadows. Students spend a day measuring and recording the length of their own shadows as the day progresses. Prior to the measuring activity, the class practised measuring different objects accurately, and discussed what they thought might happen – predicting whether the measurements would change and if they would get longer or shorter.
Students work together to measure their shadows every hour (six time points through the day), and mark the changing lengths of their shadows with chalk as well as recording the measurements in notebooks. This activity is used to reinforce the science ideas they are learning about the daily rotation of the earth, as well as building measurement skills. The students complete the activity in groups of three, which provides less confident students with support to undertake the task, and an adult also checks the accuracy of the measurements. The measurements are then collated, analysed in a class discussion, and displayed in a bar graph which they design together. As a class, they talk about why they use a bar graph and how it helps with this subject to express their ideas. The learning activity is then captured in photos and text and displayed on the wall.
5) Reflective questions for teachers
- What opportunities are there in my daily class routines to practise maths skills, develop maths knowledge, or help students make links to mathematical ideas?
- Would it be useful to map out my daily activities and plan for more intentional weaving of maths throughout the day?
- In what ways do I weave maths into other curriculum area learning? How could I do this more often?
- Am I aware of which maths games are available to me, and how they can link to my planned maths learning? What other classroom resources could I use to promote mathematical thinking and skills?
Practice area 8: Maths classes reflect the cultures of their students and their families / whānau
Maths classes that use culturally relevant materials and contexts make it easier for students to make sense of maths.
When this is going well, teachers draw on their good knowledge of students’ cultures and languages to tailor maths tasks. This involves purposefully linking maths discussions and problems to familiar cultural contexts and experiences. Culturally relevant maths materials, tools, and classroom displays support this learning and affirm that maths is connected to the students’ real world.
In this section, we set out why it makes a real difference when maths classes reflect the cultures of students and families. We also offer practical guidance on how teachers can put this into practice in their own classrooms.
Overview of this section
This part of the report sets out useful information about reflecting the cultures of students and families in maths. It includes:
- What is this practice area?
- Why is it important?
- What does good practice look like in real life?
- Good practice example
- Reflective questions for teachers
1) What is this practice area?
This practice area is about teachers making the most of maths lessons by reflecting the cultures of their students. This can be through the choice of tasks, the scenarios used for problem solving, or the materials used in teaching and learning. Teachers can draw their knowledge about students’ cultures and contexts in their decision-making about how to organise their class, how they support classroom interactions, and how they use resources to present maths ideas to their students.
The key teaching practices discussed in this section are:
|
a) teachers demonstrate and help all students make connections between maths and te ao Māori |
|
b) teachers ensure maths tasks include contexts, content, or approaches that are culturally relevant to students |
|
c) teachers use the classroom environment to promote interest in maths through cultural contexts, symbols, materials, and artefacts. |
2) Why is this important?
Students find maths more relevant and interesting when maths tasks are clearly linked to their culture, language, and home experiences. In maths contexts, this is about connecting problems, tasks, and materials to students’ everyday lives at home and in the community.xcvi As well as supporting interest and engagement, using familiar contexts also reduces the ‘cognitive load’ for students: all their focus can be on understanding the maths problem – rather than also trying to make sense of an unfamiliar context. Culturally responsive teaching is becoming more and more crucial, as Aotearoa New Zealand continues to grow in ethnic and linguistic diversity.xcvii
Reflecting students’ cultures and values in maths also helps to communicate to students a key aspect about the nature of maths - maths is embedded in and relevant to every culture. This can help to strengthen their sense of identity as successful maths students.
“If a child knows about something, then they can relate a maths problem back to themselves.” – Teacher
“Children see that their cultural backgrounds are powerful, and that maths is all around them in their lives.” – Teacher
“Tasks embedded in real-life contexts have high motivational power; students are most easily engaged with problems that are taken from their everyday lives.” – OECD, 2016xcviii
3) What does good practice look like in real life?
As part of this study, we talked to teachers and school leaders about the strategies that have worked well in their experience. We’ve collected their ideas and strategies here. It is important to reflect carefully about which of these will benefit each school’s unique community and context. No strategies are one-size-fits-all so all these strategies won’t be the right fit for everyone.
The key teacher practices that we focus on are:
- teachers demonstrate and help all students make connections between maths and te ao Māori
- teachers ensure maths tasks include contexts, content, or approaches that are culturally relevant to students
- teachers use the classroom environment to promote interest in maths through cultural contexts, symbols, materials, and artefacts.
a) Teachers demonstrate and help all students make connections between maths and te ao Māori
Teachers in Aotearoa New Zealand teach in a bicultural context. It is expected and normal that teachers will have knowledge and skills in te reo me ngā tikanga Māori, and enact Te Tiriti o Waitangi in all teaching and learning interactions.xcix In a maths context, this supports all students to make sense of maths in relation to their own lived context as students in Aotearoa, and supports Māori students to make useful links between maths concepts and their culture and language. In a maths context, teachers can draw on their skills in Te Tiriti o Waitangi-based practices by:
- linking maths concepts to components of Māori culture and language. For example, a teacher might use a hāngi scenario for a word problem on measurement and division, draw on Māori values to frame expectations for collaborative maths work, link maths concepts to navigational activities undertaken by Māori and tauiwi, or use te reo Māori for numbers, days, months, and seasons in daily warm-up activities
- supporting students to engage with Māori culture and language components, and then finding ways to integrate maths learning. Te ao Māori is seen as underpinning maths learning, rather than starting with maths and adding Māori aspects.c For example, a teacher might include a targeted discussion and exercise on patterning during a planned trip to a marae, or focus on Māori whakataukī or metaphor as a springboard for open discussion that seizes on mathematical talk opportunities
- situating maths learning within physical or practical cultural activities. For example, a teacher with a good understanding of local sites of cultural significance might organise a visit to look for patterns in flora and fauna, or measure distances, heights, and lengths of geographical features. They might explore aspects of maths in a meeting house or wharenui by looking at patterns, angles on carvings, kowhaiwhai, and estimate measurements or count rafters, length of the building or area of the floor
- ensuring Māori students have opportunities to lead in maths contexts. This could include leading group work, setting their own learning goals, working in pairs as tuakana, involving their whānau or demonstrating cultural expertise within culturally-located maths problems
- working closely with whānau Māori to define and refine teaching and learning practices, with a focus on collaboratively supporting the maths learning of their child. (See Part 9 of this report from more on partnering with families.)
Real-life strategies
|
We heard from teachers and school leaders that it works well to… |
|
Use the detail within te reo Māori words/ kupu to reinforce maths concepts. For example, teachers use te reo Māori words/ kupu to reinforce place value concepts – “tekau ma rua” for 12 shows it is made up of 10+2, or to discuss a shape’s attributes – “tapa-wha” for square emphasises the four (wha) sides. Teachers also regularly use te reo Māori words/ kupu for colours, and when counting or reading numbers. |
|
Use tuakana-teina approaches to promote maths learning. In the classes we visited, teachers encourage their students to provide support for other students, which we heard is especially successful in schools with high numbers of Māori and Pacific students. In these classrooms, we heard that sharing of ideas and working together is normalised. Teachers clarify to students that sharing solutions is not regarded as ‘cheating’ – it is seen as a learning opportunity which supports a collective understanding. Opportunities for supporting the learning of others is often structured through strategies such as choosing a partner to work with, turn and talk, think-pair-share, or forming small or social groups. |
|
Link maths learning to cultural stories. Teachers use news stories, events, legends, myths, or historical contexts, as a platform to discuss and illustrate maths concepts. For example, a teacher uses a journal story about a hāngi to prompt a word problem involving multiplication and ratios.ci |
|
Incorporate tikanga Māori into maths. For example, teachers deliberately promote values such as manaakitanga, kaitiakitanga, and rangatiratanga through maths activities and in setting up class rules for participating in group maths work. |
Practical example: Māori cultural expertise and understandings
Tī rākau (a Māori stick game) is the context for maths learning about patterning.
The teacher starts the session by supporting students to make links to the history and cultural purposes of tī rākau through videos and discussion. Then the class practises repeating clapping patterns, movement patterns, and body percussion patterns within warm-up activities. Students have previously looked at repeating elements in cultural patterns such as tukutuku, kowhaiwhai, or tapa cloth (siapo, ngatu, hiapo).
The teacher introduces a maths task where students create their own tī rākau rhythm, to accompany the waiata E Pāpā Waiari Māori. They practice alongside peers and then record their rhythm visually on rhythm cards, with numbered steps. The teacher supports students to describe their thinking with targeted questions:
Teacher: Tell me about your pattern.
Student: My pattern goes boom, clap, bang, shake right, shake left.
Teacher: What action is number 12 in this pattern? How do you know?
Student: Well, there are five actions in my pattern (Student points to her pattern cards). Shake left is five and 10. So, boom is 11 and clap is 12.
Teacher: What action is number 53 in this pattern? How do you know?
Student: Well, there are five actions in my pattern. I know that every 5 is a left shake. I know that 10 x 5 = 50. 50 is a left shake and so 3 more is 53. So, 53 is bang.
- Adapted from the ‘Pattern Makers’ exercise and resources on tahurangi.education.govt.nzcii
b) Teachers ensure maths tasks include contexts, content, or approaches that are culturally relevant to students
Students feel more connected to their learning when they see their home lives and cultural contexts reflected in what and how they learn. Teachers can help students to connect to their maths tasks by situating them in familiar cultural rituals, languages, or cultural events.
“The school is very diverse, so we use what the students are familiar with in their household.” – Teacher
“In summary: introduce the context in the real world, locate it with the children, then add the maths.” – Teacher
Example:
"[Year 1 student’s name] was teaching his friend how to make poi rope.
He cut 16 pieces of wool to make a four-plait braid.
He needed another 5 to make the tassel at the end.
How many pieces of wool is his friend going to need so she can make the same?" – Year 1-2 classroom activity
Real-life strategies
|
We heard from teachers and school leaders that it works well to… |
|
Use familiar cultural experiences and events within maths problems. Many teachers that we interviewed use what they have learnt about the cultures of students to put together tailored, relevant contexts for maths problems and tasks. They find that this is a valuable strategy for drawing students into maths tasks, and creating engaging maths-based discussion among peers. For example, a teacher shares that using Tongan food as the topic of a maths word problem is useful for grounding the maths in a meaningful context, with the added benefit of prompting their Tongan students to lead a discussion among their classmates. “All the Tongan kids can be experts.” (Teacher) |
|
Share resources that are culturally relevant across the teaching team. In one school, teachers use exemplars of maths problems which relate to the main cultures in their school, and translate key maths concepts in students’ home languages. |
|
Link maths learning to cultural stories. This involves using news stories, events, legends, myths, or historical contexts, as a platform to discuss and illustrate maths concepts. For example, teachers use journal stories about hāngi, turangawaewae, tivaevae, or picture books with cultural contexts to start conversations that lead into culturally-relevant maths problems. |
|
Use students’ names in maths problems. Teachers spoke to us about how they deliberately use student’s names and their home experiences in word problems. “Children really enjoy when their name is in the word problem – it really draws them in, and the connection helps them focus. They feel they own the problem.” (Teacher) |
|
Use words from the home or heritage languages of the students to express key maths ideas. “It’s important that maths vocab reflects the diverse nature of children in our classrooms. Many children come here with speech and language difficulties, but they bring cultural competency that is utilised in the learning. For example, probability words like ‘likely’ and ‘possible’ can be translated really easily and used to describe everyday cultural activities.” (Teacher) |
c) Teachers use the classroom environment to promote interest in maths through cultural contexts, symbols, materials, and artefacts
Incorporating visible connections to students’ cultural contexts help to make maths class inviting and relevant to students. Teachers might do this through, for example, classroom wall displays or by incorporating symbols and artefacts as materials alongside maths ideas. It is important to first work with students and families to understand the meaning, history, and cultural value of artefacts when considering using them for maths.
Real-life strategies
|
We heard from teachers and school leaders that it works well to… |
|
Display cultural artefacts that have patterns. Some classes ERO visited use wall and table displays, for example siapo mats and tapa cloths with patterns that illustrate geometry and algebra concepts. Teachers reference these mats and cloths during maths lessons, and students refer to them to identify repeated patterns or shapes. These can also be used as a springboard for ‘maths talk’ about patterns. For example, students are asked how many leaves a pattern will have when turning a tivaevae cushion design into a larger quilt. Students find a rule for the number of leaves at any position in a tivaevae pattern and use that rule to make predictions about how many leaves will be in the larger quilt.ciii |
|
Celebrate examples of maths achievements from a range of cultures. Teachers highlight culturally located examples of navigation, measuring tools, as well as mathematicians and maths achievements of key people in the local area, through visual displays. |
|
Incorporate visual symbols from a range of cultures into maths displays and activities. We observed wall displays which incorporate designs from Māori and Pacific cultures represented in the class. Displays included tukutuku and kowhaiwhai patterns, tivaevae patterns, and koru and taaniko symbols. Another class works with chalk in the playground to draw and describe numbers and patterns related to Diwali symbols. |
|
Use photographs of community cultural events or practices. One teacher uses the regular community market stalls to make links to maths ideas. She shows photographs of the market and asks, “Have you been to the night market and seen this food?” The teacher uses the market scene to frame maths problems for the class to solve. Other teachers share that using examples or photographs of preparation for culturally based events such as hangi or umu can generate rich contexts to engage in maths - measuring, multiplication and division, and more. |
4) Good practice example
In one school with high numbers of Pacific students, teachers focus on selecting contexts that will be familiar to students. They make frequent use of foods and social events that are relevant to the Pacific communities on their roll.
Cultural artefacts such as celebratory ‘lolly lei’ are used as contexts for counting, multiplication, and patterning. Teachers note that they discuss ways to ensure that such artefacts are used respectfully, often using photos or other materials to represent items, rather than the items themselves.
One maths unit is around panekeke (Samoan pancakes) which are well known to many of their Pacific students. When first introducing the topic, they hold a free-flowing conversation with the students about panekeke, “to ground the maths in the students’ home lives.” They ask, “Who has had it, how do they make it, where do they get it from?” The discussions then move into maths ideas: measurement, fractions, addition, and multiplication (quantities and ratios of people and pancakes) all in the context of mixing, baking, and eating panekeke.
In another session, White Sunday celebrations are used this to surface hidden maths. For example, they discuss the different numbers of groups attending, and the quantities of supplies for meals. The context of White Sunday is also used for setting maths word problems, for example: Nearly all of Sione’s aiga attended White Sunday at his church last week. Here are the different people in his family [using photographs or diagrams]. How many altogether? Half of the 150 people at the church were children – how many children were there?
Teachers note how these contexts for learning have an extra benefit of raising the profile of students who know a lot about the cultural aspects being discussed. “It gives the impression that teacher cares and that their world is important.”
5) Reflective questions for teachers
- How much do I know about the cultural contexts and knowledge my students bring to the learning process? How could I use this information in maths contexts?
- What are the deliberate ways in which I incorporate the cultures, contexts and cultural knowledge of my students into maths?
- How do I ensure my teaching approaches are inclusive of all my students and respond to their cultural contexts and backgrounds? How do I know if I’m successful?
Maths classes that use culturally relevant materials and contexts make it easier for students to make sense of maths.
When this is going well, teachers draw on their good knowledge of students’ cultures and languages to tailor maths tasks. This involves purposefully linking maths discussions and problems to familiar cultural contexts and experiences. Culturally relevant maths materials, tools, and classroom displays support this learning and affirm that maths is connected to the students’ real world.
In this section, we set out why it makes a real difference when maths classes reflect the cultures of students and families. We also offer practical guidance on how teachers can put this into practice in their own classrooms.
Overview of this section
This part of the report sets out useful information about reflecting the cultures of students and families in maths. It includes:
- What is this practice area?
- Why is it important?
- What does good practice look like in real life?
- Good practice example
- Reflective questions for teachers
1) What is this practice area?
This practice area is about teachers making the most of maths lessons by reflecting the cultures of their students. This can be through the choice of tasks, the scenarios used for problem solving, or the materials used in teaching and learning. Teachers can draw their knowledge about students’ cultures and contexts in their decision-making about how to organise their class, how they support classroom interactions, and how they use resources to present maths ideas to their students.
The key teaching practices discussed in this section are:
|
a) teachers demonstrate and help all students make connections between maths and te ao Māori |
|
b) teachers ensure maths tasks include contexts, content, or approaches that are culturally relevant to students |
|
c) teachers use the classroom environment to promote interest in maths through cultural contexts, symbols, materials, and artefacts. |
2) Why is this important?
Students find maths more relevant and interesting when maths tasks are clearly linked to their culture, language, and home experiences. In maths contexts, this is about connecting problems, tasks, and materials to students’ everyday lives at home and in the community.xcvi As well as supporting interest and engagement, using familiar contexts also reduces the ‘cognitive load’ for students: all their focus can be on understanding the maths problem – rather than also trying to make sense of an unfamiliar context. Culturally responsive teaching is becoming more and more crucial, as Aotearoa New Zealand continues to grow in ethnic and linguistic diversity.xcvii
Reflecting students’ cultures and values in maths also helps to communicate to students a key aspect about the nature of maths - maths is embedded in and relevant to every culture. This can help to strengthen their sense of identity as successful maths students.
“If a child knows about something, then they can relate a maths problem back to themselves.” – Teacher
“Children see that their cultural backgrounds are powerful, and that maths is all around them in their lives.” – Teacher
“Tasks embedded in real-life contexts have high motivational power; students are most easily engaged with problems that are taken from their everyday lives.” – OECD, 2016xcviii
3) What does good practice look like in real life?
As part of this study, we talked to teachers and school leaders about the strategies that have worked well in their experience. We’ve collected their ideas and strategies here. It is important to reflect carefully about which of these will benefit each school’s unique community and context. No strategies are one-size-fits-all so all these strategies won’t be the right fit for everyone.
The key teacher practices that we focus on are:
- teachers demonstrate and help all students make connections between maths and te ao Māori
- teachers ensure maths tasks include contexts, content, or approaches that are culturally relevant to students
- teachers use the classroom environment to promote interest in maths through cultural contexts, symbols, materials, and artefacts.
a) Teachers demonstrate and help all students make connections between maths and te ao Māori
Teachers in Aotearoa New Zealand teach in a bicultural context. It is expected and normal that teachers will have knowledge and skills in te reo me ngā tikanga Māori, and enact Te Tiriti o Waitangi in all teaching and learning interactions.xcix In a maths context, this supports all students to make sense of maths in relation to their own lived context as students in Aotearoa, and supports Māori students to make useful links between maths concepts and their culture and language. In a maths context, teachers can draw on their skills in Te Tiriti o Waitangi-based practices by:
- linking maths concepts to components of Māori culture and language. For example, a teacher might use a hāngi scenario for a word problem on measurement and division, draw on Māori values to frame expectations for collaborative maths work, link maths concepts to navigational activities undertaken by Māori and tauiwi, or use te reo Māori for numbers, days, months, and seasons in daily warm-up activities
- supporting students to engage with Māori culture and language components, and then finding ways to integrate maths learning. Te ao Māori is seen as underpinning maths learning, rather than starting with maths and adding Māori aspects.c For example, a teacher might include a targeted discussion and exercise on patterning during a planned trip to a marae, or focus on Māori whakataukī or metaphor as a springboard for open discussion that seizes on mathematical talk opportunities
- situating maths learning within physical or practical cultural activities. For example, a teacher with a good understanding of local sites of cultural significance might organise a visit to look for patterns in flora and fauna, or measure distances, heights, and lengths of geographical features. They might explore aspects of maths in a meeting house or wharenui by looking at patterns, angles on carvings, kowhaiwhai, and estimate measurements or count rafters, length of the building or area of the floor
- ensuring Māori students have opportunities to lead in maths contexts. This could include leading group work, setting their own learning goals, working in pairs as tuakana, involving their whānau or demonstrating cultural expertise within culturally-located maths problems
- working closely with whānau Māori to define and refine teaching and learning practices, with a focus on collaboratively supporting the maths learning of their child. (See Part 9 of this report from more on partnering with families.)
Real-life strategies
|
We heard from teachers and school leaders that it works well to… |
|
Use the detail within te reo Māori words/ kupu to reinforce maths concepts. For example, teachers use te reo Māori words/ kupu to reinforce place value concepts – “tekau ma rua” for 12 shows it is made up of 10+2, or to discuss a shape’s attributes – “tapa-wha” for square emphasises the four (wha) sides. Teachers also regularly use te reo Māori words/ kupu for colours, and when counting or reading numbers. |
|
Use tuakana-teina approaches to promote maths learning. In the classes we visited, teachers encourage their students to provide support for other students, which we heard is especially successful in schools with high numbers of Māori and Pacific students. In these classrooms, we heard that sharing of ideas and working together is normalised. Teachers clarify to students that sharing solutions is not regarded as ‘cheating’ – it is seen as a learning opportunity which supports a collective understanding. Opportunities for supporting the learning of others is often structured through strategies such as choosing a partner to work with, turn and talk, think-pair-share, or forming small or social groups. |
|
Link maths learning to cultural stories. Teachers use news stories, events, legends, myths, or historical contexts, as a platform to discuss and illustrate maths concepts. For example, a teacher uses a journal story about a hāngi to prompt a word problem involving multiplication and ratios.ci |
|
Incorporate tikanga Māori into maths. For example, teachers deliberately promote values such as manaakitanga, kaitiakitanga, and rangatiratanga through maths activities and in setting up class rules for participating in group maths work. |
Practical example: Māori cultural expertise and understandings
Tī rākau (a Māori stick game) is the context for maths learning about patterning.
The teacher starts the session by supporting students to make links to the history and cultural purposes of tī rākau through videos and discussion. Then the class practises repeating clapping patterns, movement patterns, and body percussion patterns within warm-up activities. Students have previously looked at repeating elements in cultural patterns such as tukutuku, kowhaiwhai, or tapa cloth (siapo, ngatu, hiapo).
The teacher introduces a maths task where students create their own tī rākau rhythm, to accompany the waiata E Pāpā Waiari Māori. They practice alongside peers and then record their rhythm visually on rhythm cards, with numbered steps. The teacher supports students to describe their thinking with targeted questions:
Teacher: Tell me about your pattern.
Student: My pattern goes boom, clap, bang, shake right, shake left.
Teacher: What action is number 12 in this pattern? How do you know?
Student: Well, there are five actions in my pattern (Student points to her pattern cards). Shake left is five and 10. So, boom is 11 and clap is 12.
Teacher: What action is number 53 in this pattern? How do you know?
Student: Well, there are five actions in my pattern. I know that every 5 is a left shake. I know that 10 x 5 = 50. 50 is a left shake and so 3 more is 53. So, 53 is bang.
- Adapted from the ‘Pattern Makers’ exercise and resources on tahurangi.education.govt.nzcii
b) Teachers ensure maths tasks include contexts, content, or approaches that are culturally relevant to students
Students feel more connected to their learning when they see their home lives and cultural contexts reflected in what and how they learn. Teachers can help students to connect to their maths tasks by situating them in familiar cultural rituals, languages, or cultural events.
“The school is very diverse, so we use what the students are familiar with in their household.” – Teacher
“In summary: introduce the context in the real world, locate it with the children, then add the maths.” – Teacher
Example:
"[Year 1 student’s name] was teaching his friend how to make poi rope.
He cut 16 pieces of wool to make a four-plait braid.
He needed another 5 to make the tassel at the end.
How many pieces of wool is his friend going to need so she can make the same?" – Year 1-2 classroom activity
Real-life strategies
|
We heard from teachers and school leaders that it works well to… |
|
Use familiar cultural experiences and events within maths problems. Many teachers that we interviewed use what they have learnt about the cultures of students to put together tailored, relevant contexts for maths problems and tasks. They find that this is a valuable strategy for drawing students into maths tasks, and creating engaging maths-based discussion among peers. For example, a teacher shares that using Tongan food as the topic of a maths word problem is useful for grounding the maths in a meaningful context, with the added benefit of prompting their Tongan students to lead a discussion among their classmates. “All the Tongan kids can be experts.” (Teacher) |
|
Share resources that are culturally relevant across the teaching team. In one school, teachers use exemplars of maths problems which relate to the main cultures in their school, and translate key maths concepts in students’ home languages. |
|
Link maths learning to cultural stories. This involves using news stories, events, legends, myths, or historical contexts, as a platform to discuss and illustrate maths concepts. For example, teachers use journal stories about hāngi, turangawaewae, tivaevae, or picture books with cultural contexts to start conversations that lead into culturally-relevant maths problems. |
|
Use students’ names in maths problems. Teachers spoke to us about how they deliberately use student’s names and their home experiences in word problems. “Children really enjoy when their name is in the word problem – it really draws them in, and the connection helps them focus. They feel they own the problem.” (Teacher) |
|
Use words from the home or heritage languages of the students to express key maths ideas. “It’s important that maths vocab reflects the diverse nature of children in our classrooms. Many children come here with speech and language difficulties, but they bring cultural competency that is utilised in the learning. For example, probability words like ‘likely’ and ‘possible’ can be translated really easily and used to describe everyday cultural activities.” (Teacher) |
c) Teachers use the classroom environment to promote interest in maths through cultural contexts, symbols, materials, and artefacts
Incorporating visible connections to students’ cultural contexts help to make maths class inviting and relevant to students. Teachers might do this through, for example, classroom wall displays or by incorporating symbols and artefacts as materials alongside maths ideas. It is important to first work with students and families to understand the meaning, history, and cultural value of artefacts when considering using them for maths.
Real-life strategies
|
We heard from teachers and school leaders that it works well to… |
|
Display cultural artefacts that have patterns. Some classes ERO visited use wall and table displays, for example siapo mats and tapa cloths with patterns that illustrate geometry and algebra concepts. Teachers reference these mats and cloths during maths lessons, and students refer to them to identify repeated patterns or shapes. These can also be used as a springboard for ‘maths talk’ about patterns. For example, students are asked how many leaves a pattern will have when turning a tivaevae cushion design into a larger quilt. Students find a rule for the number of leaves at any position in a tivaevae pattern and use that rule to make predictions about how many leaves will be in the larger quilt.ciii |
|
Celebrate examples of maths achievements from a range of cultures. Teachers highlight culturally located examples of navigation, measuring tools, as well as mathematicians and maths achievements of key people in the local area, through visual displays. |
|
Incorporate visual symbols from a range of cultures into maths displays and activities. We observed wall displays which incorporate designs from Māori and Pacific cultures represented in the class. Displays included tukutuku and kowhaiwhai patterns, tivaevae patterns, and koru and taaniko symbols. Another class works with chalk in the playground to draw and describe numbers and patterns related to Diwali symbols. |
|
Use photographs of community cultural events or practices. One teacher uses the regular community market stalls to make links to maths ideas. She shows photographs of the market and asks, “Have you been to the night market and seen this food?” The teacher uses the market scene to frame maths problems for the class to solve. Other teachers share that using examples or photographs of preparation for culturally based events such as hangi or umu can generate rich contexts to engage in maths - measuring, multiplication and division, and more. |
4) Good practice example
In one school with high numbers of Pacific students, teachers focus on selecting contexts that will be familiar to students. They make frequent use of foods and social events that are relevant to the Pacific communities on their roll.
Cultural artefacts such as celebratory ‘lolly lei’ are used as contexts for counting, multiplication, and patterning. Teachers note that they discuss ways to ensure that such artefacts are used respectfully, often using photos or other materials to represent items, rather than the items themselves.
One maths unit is around panekeke (Samoan pancakes) which are well known to many of their Pacific students. When first introducing the topic, they hold a free-flowing conversation with the students about panekeke, “to ground the maths in the students’ home lives.” They ask, “Who has had it, how do they make it, where do they get it from?” The discussions then move into maths ideas: measurement, fractions, addition, and multiplication (quantities and ratios of people and pancakes) all in the context of mixing, baking, and eating panekeke.
In another session, White Sunday celebrations are used this to surface hidden maths. For example, they discuss the different numbers of groups attending, and the quantities of supplies for meals. The context of White Sunday is also used for setting maths word problems, for example: Nearly all of Sione’s aiga attended White Sunday at his church last week. Here are the different people in his family [using photographs or diagrams]. How many altogether? Half of the 150 people at the church were children – how many children were there?
Teachers note how these contexts for learning have an extra benefit of raising the profile of students who know a lot about the cultural aspects being discussed. “It gives the impression that teacher cares and that their world is important.”
5) Reflective questions for teachers
- How much do I know about the cultural contexts and knowledge my students bring to the learning process? How could I use this information in maths contexts?
- What are the deliberate ways in which I incorporate the cultures, contexts and cultural knowledge of my students into maths?
- How do I ensure my teaching approaches are inclusive of all my students and respond to their cultural contexts and backgrounds? How do I know if I’m successful?
Practice area 9: Teachers work in partnership with families / whānau to support maths learning
This practice area is about teachers working with families and whānau to support their children’s maths learning.
When this is going well, teachers regularly communicate with families/whānau about what maths learning looks like, and how well their children are progressing in maths. They also provide practical ideas for how families/whānau can support maths learning at home and suggest ways they can be involved in maths programmes. Creating partnerships means students’ learning opportunities are maximised and students receive consistent and positive messages about maths.
In this section, we set out why teachers should work in partnership with families/whānau specifically around maths learning. We also offer practical guidance on how teachers can grow this practice within their own school.
Overview of this section
This part of the report sets out useful information about how teachers can work in partnership with families/whānau to support maths learning. It includes:
- What is this practice area?
- Why is this important?
- What does good practice look like in real life?
- Good practice example
- Reflective questions for teachers
1) What is this practice area?
This practice area is about teachers working closely with families/whānau to maximise maths teaching and learning. This includes finding opportunities to learn about their maths attitudes and practices that are happening at home, showing or talking about what maths looks like in their child’s classroom, and offering ideas and resources so that they can support their child with maths in their home and community.
The key teaching practices discussed in this section are:
|
a) teachers talk about maths learning with families/whānau |
|
b) teachers provide maths information and resources to families/whānau to reinforce what is being learnt in the classroom |
2) Why is this important?
We know that learning-focused relationships with families/whānau have a positive impact on students’ learning outcomes. This area of teacher practice is strongly emphasised in Aotearoa New Zealand-based research and guiding documents.civ
As this report outlines, it’s important for Year 1-3 maths students to:
- see themselves as capable maths students
- experience maths concepts and ideas in a range of contexts
- have opportunities to practise and use maths in ways that feel relevant to them.
Strong home-school partnerships help with all of these. Teachers can work with families/whānau to ensure that their children benefit from shared, positive messages about their maths capability and the value of maths learning. (Hopefully moving away from narratives of “hating maths” or “maths just being for some people.”) Sharing information and resources related to current maths teaching helps ensure that there are meaningful maths activities and discussions happening across the home and school settings as well as reinforce and embed the learning occurring in the classroom. Teachers working in partnership with families/whānau offers students a well-aligned maths programme beyond the classroom.
Students’ attitudes and beliefs about maths are influenced by their parents, families, and whānau.cv It is not uncommon to hear parents say, “I didn’t like maths at school” or “I am hopeless at mathematics.” Talking to family/whānau members about their own experiences of maths can provide useful information about home influences on a students’ maths identities. It’s important that families/whānau recognise that how they see and talk about maths influences their child.
“Parental perspectives and engagement is an important indicator of children’s attitudes towards mathematics and their achievement.” - O’Neill et. al., 2023cvi
What do your students’ families/whānau think of maths?
Parental beliefs and attitudes towards maths can directly impact on students’ engagement and enjoyment of maths,cvii which means families/whānau have the opportunity to make a significant positive difference to their child’s maths learning. However, we know that maths often causes anxiety in adults, particularly if they lack confidence or have not had positive learning experiences in the past. When teachers find opportunities to talk with families/whānau s about maths learning, involve them in their maths programme and provide suggestions for supporting learning at home, this helps to demystify maths and make meaningful connections for families/whānau and students.
It is important for teachers and families/whānau work together to promote student’s positive engagement, modelled and supported by adults in both contexts.cviii
3) What does good practice look like in real life?
As part of this study, we talked to teachers and school leaders about the strategies that have worked well in their experience. We’ve collected their ideas and strategies here. It is important to reflect carefully about which of these will benefit each school’s unique community and context. No strategies are one-size-fits-all so all these strategies won’t be the right fit for everyone.
The key teacher practices that we focus on are:
- teachers talk about maths with families/whānau
- teachers provide information and resources for families/whānau as well as reinforce and embed the learning occurring in the classroom.
a) Teachers talk about maths with families/whānau
Teachers need to take an active role in developing relationships with families/whānau that include a focus on supporting maths learning. This requires teachers to take time to understand the maths experiences and practices of families/whānau, talk through any questions they may have, and agree on shared messages about maths learning. When maths is a regular topic of conversation, it’s easier for families/whānau to remember the value of at-home maths talk and maths experiences.
“For a true partnership, there needs to be communication and shared understandings between the three parties. It is important for parents (and whānau) to learn about the mathematics taught in the classroom, but it is equally important for teachers to know about children's mathematical experiences at home.” - NZMathscix
Real-life strategies
|
We heard from teachers and school leaders that it works well to… |
|
Use a combination of formal and informal settings for maths conversations. Teachers kōrero with families/whānau about maths at formalised events (such as parent-teacher meetings) and informal school or sporting events, as well as impromptu conversations at the beginning or end of the day. |
|
Focus on listening to families as a first step. At one school, teachers use a staggered approach to build relationships with families over a series of hui. Their first engagement with a family/whānau is an interview, led by the family/whānau, and where the teacher and school leaders participate primarily as listeners while families/whānau share information and aspirations. A second follow-up meeting is set up to develop plans for learning. At the beginning and end of each term, a whole day is assigned for learning conversations. On the first day of each term, the conversations are focused on the family/whānau aspirations for maths learning progress. At the end of term, they focus on the maths progress made. |
|
Include students in whānau-teacher meetings. Some schools told us how students use these catch-ups to show their families/whānau their maths learning they have been enjoying in class. |
|
Use digital tools to share maths learning with families/whānau. Most schools ERO visited use digital platforms to share learning and build learning partnerships with families/whānau. These platforms are often managed independently by students to make a record of, or to reflect on, their learning. Students take photographs of their work or their environment, make videos, or write descriptions of their learning activities. Teachers and peers provide supportive comments, and families/whānau add comments and examples of at-home learning. These learning snapshots help keep maths learning top-of-mind for families. |
|
Keep families/whānau updated about the maths programme through schoolwide hui. Schools that we visited do this in various ways, often through presentations to families/whānau. These are sometimes led by school leaders or external experts. |
|
Provide opportunities for families/whānau to contribute resources and expertise to the class maths programme. Teachers spoke about ways in which they invite families/whānau to support their maths teaching through contributing cultural artefacts, sharing how they use maths within their work, talking to students about a cultural event as a context for learning (e.g. preparing food for a social gathering), or by acting as parent helpers for students within class maths time. |
|
Invite families/whānau into maths classes. Some schools hold open days for families/whānau to attend during maths time. These sessions demonstrate how teachers and students use equipment, how students work together, the role of games as part of a teaching session, and how teachers provide explicit teaching. |
b) Teachers provide information and resources to families/whānau to reinforce what is being learnt in the classroom
Teachers can support students’ maths achievement by actively encouraging maths learning at home. Teachers might provide facts or tips about doing maths, or activities and games. In the early years of school, it’s important to focus on activities that families/whānau and their children can do together.
It’s useful to share ideas that capitalise on the learning opportunities that are already happening within their usual family/whānau activities and local community. This can involve discussing how to ‘see’ or practise maths in everyday routines, such as brushing teeth. Home maths activities help to deepen maths understandings through authentic experiences, and offer opportunities for experiencing enjoyment with maths. Providing suggestions and activities to families/whānau can also mean that the same language and resources are being used across both settings, which reinforces maths language for students.
"Involving the student’s whānau/family in maths learning experiences and successes, helps to show the value in maths, make it more meaningful and connected to their everyday lives, and can promote curiosity and positive attitudes to maths.” – Papadopoulos, 2017cx
Real-life strategies
|
We heard from teachers and school leaders that it works well to… |
|
Showcase at-home maths learning in workshops for families/whānau. Some schools run evening or daytime sessions for families/whānau prior to beginning a new unit of work, that include a focus on how the unit could be supported at home. In workshops, teachers outline the key maths concepts, supporting materials, and examples of activities students will be encountering in the unit. Some of these sessions are run as active learning workshops where families/whānau manipulate equipment and play games. Teachers and families/whānau also consider ways that their home environment or home practices can be used to make links to maths learning. Teachers shared that these sessions have helped parents to build their own understandings of maths concepts and processes so that they can better support learning at home. |
|
Develop ‘home kits’ for families/whānau to use with their children. In one school, this was a practice that started during Covid-19 lockdowns, and was retained when teachers noticed the positive impacts. Maths home kits are regularly compiled by the teaching team. These include a list of suggestions for activities and games to play as a family/whānau, that relate to current classroom maths learning. Ideas for activities include such things as:
|
4) Good practice example
At one school, with a high Pacific population, teachers work with their parents, whānau and aiga in a range of ways to promote their interest and engagement in maths.
Teachers provide afternoon and evening maths workshops, after checking with families/whānau about their preferred times. These workshops relate to a current maths focus, such as fractions. The workshops include demonstrations of fraction activities and equipment as well as ideas for learning about fractions at home. Teachers provide printouts of activities and fraction boards for home use.
At school meetings the school sets up a stall which displays maths learning, videos of learning sessions, and copies of tasks and games for families/whānau to take home.
Open days are held where parents/whānau are invited in to observe maths in action. Teachers include take home packs of related maths activities for families. These include:
- copies of tasks being used in the maths sessions
- laminated hundreds boards
- games and activities to do at home.
Individual learning reports to parents/whānau include specific suggestions for “Ways to help at home.”
A school holiday programme, run with professional learning experts, includes a strong focus on maths activities. This helps to promote interest and enjoyment, and raises the profile of maths for students and families/whānau.
5) Reflective questions for teachers
- In what ways do I support families/whānau to know about the maths learning and progress of their child?
- Do I know how my students’ families/whānau feel about maths? What questions could I ask?
- How can I support families/whānau to make connections to maths through authentic home contexts? Would they appreciate more or clearer guidance?
- How can I draw on the knowledge and expertise of families/whānau within my maths programme
- What resources can I provide for families/whānau to help them connect with the maths learning that’s happening in the classroom?
This practice area is about teachers working with families and whānau to support their children’s maths learning.
When this is going well, teachers regularly communicate with families/whānau about what maths learning looks like, and how well their children are progressing in maths. They also provide practical ideas for how families/whānau can support maths learning at home and suggest ways they can be involved in maths programmes. Creating partnerships means students’ learning opportunities are maximised and students receive consistent and positive messages about maths.
In this section, we set out why teachers should work in partnership with families/whānau specifically around maths learning. We also offer practical guidance on how teachers can grow this practice within their own school.
Overview of this section
This part of the report sets out useful information about how teachers can work in partnership with families/whānau to support maths learning. It includes:
- What is this practice area?
- Why is this important?
- What does good practice look like in real life?
- Good practice example
- Reflective questions for teachers
1) What is this practice area?
This practice area is about teachers working closely with families/whānau to maximise maths teaching and learning. This includes finding opportunities to learn about their maths attitudes and practices that are happening at home, showing or talking about what maths looks like in their child’s classroom, and offering ideas and resources so that they can support their child with maths in their home and community.
The key teaching practices discussed in this section are:
|
a) teachers talk about maths learning with families/whānau |
|
b) teachers provide maths information and resources to families/whānau to reinforce what is being learnt in the classroom |
2) Why is this important?
We know that learning-focused relationships with families/whānau have a positive impact on students’ learning outcomes. This area of teacher practice is strongly emphasised in Aotearoa New Zealand-based research and guiding documents.civ
As this report outlines, it’s important for Year 1-3 maths students to:
- see themselves as capable maths students
- experience maths concepts and ideas in a range of contexts
- have opportunities to practise and use maths in ways that feel relevant to them.
Strong home-school partnerships help with all of these. Teachers can work with families/whānau to ensure that their children benefit from shared, positive messages about their maths capability and the value of maths learning. (Hopefully moving away from narratives of “hating maths” or “maths just being for some people.”) Sharing information and resources related to current maths teaching helps ensure that there are meaningful maths activities and discussions happening across the home and school settings as well as reinforce and embed the learning occurring in the classroom. Teachers working in partnership with families/whānau offers students a well-aligned maths programme beyond the classroom.
Students’ attitudes and beliefs about maths are influenced by their parents, families, and whānau.cv It is not uncommon to hear parents say, “I didn’t like maths at school” or “I am hopeless at mathematics.” Talking to family/whānau members about their own experiences of maths can provide useful information about home influences on a students’ maths identities. It’s important that families/whānau recognise that how they see and talk about maths influences their child.
“Parental perspectives and engagement is an important indicator of children’s attitudes towards mathematics and their achievement.” - O’Neill et. al., 2023cvi
What do your students’ families/whānau think of maths?
Parental beliefs and attitudes towards maths can directly impact on students’ engagement and enjoyment of maths,cvii which means families/whānau have the opportunity to make a significant positive difference to their child’s maths learning. However, we know that maths often causes anxiety in adults, particularly if they lack confidence or have not had positive learning experiences in the past. When teachers find opportunities to talk with families/whānau s about maths learning, involve them in their maths programme and provide suggestions for supporting learning at home, this helps to demystify maths and make meaningful connections for families/whānau and students.
It is important for teachers and families/whānau work together to promote student’s positive engagement, modelled and supported by adults in both contexts.cviii
3) What does good practice look like in real life?
As part of this study, we talked to teachers and school leaders about the strategies that have worked well in their experience. We’ve collected their ideas and strategies here. It is important to reflect carefully about which of these will benefit each school’s unique community and context. No strategies are one-size-fits-all so all these strategies won’t be the right fit for everyone.
The key teacher practices that we focus on are:
- teachers talk about maths with families/whānau
- teachers provide information and resources for families/whānau as well as reinforce and embed the learning occurring in the classroom.
a) Teachers talk about maths with families/whānau
Teachers need to take an active role in developing relationships with families/whānau that include a focus on supporting maths learning. This requires teachers to take time to understand the maths experiences and practices of families/whānau, talk through any questions they may have, and agree on shared messages about maths learning. When maths is a regular topic of conversation, it’s easier for families/whānau to remember the value of at-home maths talk and maths experiences.
“For a true partnership, there needs to be communication and shared understandings between the three parties. It is important for parents (and whānau) to learn about the mathematics taught in the classroom, but it is equally important for teachers to know about children's mathematical experiences at home.” - NZMathscix
Real-life strategies
|
We heard from teachers and school leaders that it works well to… |
|
Use a combination of formal and informal settings for maths conversations. Teachers kōrero with families/whānau about maths at formalised events (such as parent-teacher meetings) and informal school or sporting events, as well as impromptu conversations at the beginning or end of the day. |
|
Focus on listening to families as a first step. At one school, teachers use a staggered approach to build relationships with families over a series of hui. Their first engagement with a family/whānau is an interview, led by the family/whānau, and where the teacher and school leaders participate primarily as listeners while families/whānau share information and aspirations. A second follow-up meeting is set up to develop plans for learning. At the beginning and end of each term, a whole day is assigned for learning conversations. On the first day of each term, the conversations are focused on the family/whānau aspirations for maths learning progress. At the end of term, they focus on the maths progress made. |
|
Include students in whānau-teacher meetings. Some schools told us how students use these catch-ups to show their families/whānau their maths learning they have been enjoying in class. |
|
Use digital tools to share maths learning with families/whānau. Most schools ERO visited use digital platforms to share learning and build learning partnerships with families/whānau. These platforms are often managed independently by students to make a record of, or to reflect on, their learning. Students take photographs of their work or their environment, make videos, or write descriptions of their learning activities. Teachers and peers provide supportive comments, and families/whānau add comments and examples of at-home learning. These learning snapshots help keep maths learning top-of-mind for families. |
|
Keep families/whānau updated about the maths programme through schoolwide hui. Schools that we visited do this in various ways, often through presentations to families/whānau. These are sometimes led by school leaders or external experts. |
|
Provide opportunities for families/whānau to contribute resources and expertise to the class maths programme. Teachers spoke about ways in which they invite families/whānau to support their maths teaching through contributing cultural artefacts, sharing how they use maths within their work, talking to students about a cultural event as a context for learning (e.g. preparing food for a social gathering), or by acting as parent helpers for students within class maths time. |
|
Invite families/whānau into maths classes. Some schools hold open days for families/whānau to attend during maths time. These sessions demonstrate how teachers and students use equipment, how students work together, the role of games as part of a teaching session, and how teachers provide explicit teaching. |
b) Teachers provide information and resources to families/whānau to reinforce what is being learnt in the classroom
Teachers can support students’ maths achievement by actively encouraging maths learning at home. Teachers might provide facts or tips about doing maths, or activities and games. In the early years of school, it’s important to focus on activities that families/whānau and their children can do together.
It’s useful to share ideas that capitalise on the learning opportunities that are already happening within their usual family/whānau activities and local community. This can involve discussing how to ‘see’ or practise maths in everyday routines, such as brushing teeth. Home maths activities help to deepen maths understandings through authentic experiences, and offer opportunities for experiencing enjoyment with maths. Providing suggestions and activities to families/whānau can also mean that the same language and resources are being used across both settings, which reinforces maths language for students.
"Involving the student’s whānau/family in maths learning experiences and successes, helps to show the value in maths, make it more meaningful and connected to their everyday lives, and can promote curiosity and positive attitudes to maths.” – Papadopoulos, 2017cx
Real-life strategies
|
We heard from teachers and school leaders that it works well to… |
|
Showcase at-home maths learning in workshops for families/whānau. Some schools run evening or daytime sessions for families/whānau prior to beginning a new unit of work, that include a focus on how the unit could be supported at home. In workshops, teachers outline the key maths concepts, supporting materials, and examples of activities students will be encountering in the unit. Some of these sessions are run as active learning workshops where families/whānau manipulate equipment and play games. Teachers and families/whānau also consider ways that their home environment or home practices can be used to make links to maths learning. Teachers shared that these sessions have helped parents to build their own understandings of maths concepts and processes so that they can better support learning at home. |
|
Develop ‘home kits’ for families/whānau to use with their children. In one school, this was a practice that started during Covid-19 lockdowns, and was retained when teachers noticed the positive impacts. Maths home kits are regularly compiled by the teaching team. These include a list of suggestions for activities and games to play as a family/whānau, that relate to current classroom maths learning. Ideas for activities include such things as:
|
4) Good practice example
At one school, with a high Pacific population, teachers work with their parents, whānau and aiga in a range of ways to promote their interest and engagement in maths.
Teachers provide afternoon and evening maths workshops, after checking with families/whānau about their preferred times. These workshops relate to a current maths focus, such as fractions. The workshops include demonstrations of fraction activities and equipment as well as ideas for learning about fractions at home. Teachers provide printouts of activities and fraction boards for home use.
At school meetings the school sets up a stall which displays maths learning, videos of learning sessions, and copies of tasks and games for families/whānau to take home.
Open days are held where parents/whānau are invited in to observe maths in action. Teachers include take home packs of related maths activities for families. These include:
- copies of tasks being used in the maths sessions
- laminated hundreds boards
- games and activities to do at home.
Individual learning reports to parents/whānau include specific suggestions for “Ways to help at home.”
A school holiday programme, run with professional learning experts, includes a strong focus on maths activities. This helps to promote interest and enjoyment, and raises the profile of maths for students and families/whānau.
5) Reflective questions for teachers
- In what ways do I support families/whānau to know about the maths learning and progress of their child?
- Do I know how my students’ families/whānau feel about maths? What questions could I ask?
- How can I support families/whānau to make connections to maths through authentic home contexts? Would they appreciate more or clearer guidance?
- How can I draw on the knowledge and expertise of families/whānau within my maths programme
- What resources can I provide for families/whānau to help them connect with the maths learning that’s happening in the classroom?
Conclusion
Years 1-3 are when crucial maths learning happens. Teachers have the chance in these years to provide students with the foundational maths understandings that set them up for success in their future schooling and beyond. This all starts with teachers valuing maths, and being grounded in a solid grasp of maths concepts and how maths learning works.
In this report, we put research and real-life stories together to shine a light on the key ways that teachers can improve their maths teaching, to benefit our young maths students.
Early maths really matters
In the early years of primary school, teachers have the opportunity to set the scene for their young maths students. It is in these early years that students form their foundational understandings of maths concepts, and of their own capability as maths students. We know that maths is the pathway to success in many other learning areas as well as having longer-term economic benefits, which means early maths has big impacts for learning and life outcomes.
However, not all students and teachers are confident about maths. Our national achievement picture isn’t strong, and not all teachers feel prepared for engaging students in this crucial area of their schooling.
This research uses robust evidence from the global and local research base, combined with real-life insights and strategies from Aotearoa New Zealand classrooms, to clarify ‘what good looks like’ in early maths teaching. By shining a light on good practice, we hope to inspire teachers to improve their maths teaching practice.
We found two key enablers that set teachers up to do their best work
Great maths teaching needs great foundations. Teachers need to be confident in their own maths knowledge and skills so that they are ready to teach them to their students. They also need to know about what works for young students: the evidence-based teaching and learning strategies that set up the key understandings needed for this part of their maths journey. This includes being clear about the best ways to build up important maths ideas, while avoiding misunderstandings or shortcuts which negatively impact on later learning.
Teachers’ school settings set the scene for good maths practice by promoting a clear, shared understanding of the value of quality maths teaching. Schools can do this by clearly setting out what maths teaching and maths progress look like in their whole school curriculum, and supporting teacher understanding with great learning and collaboration opportunities. It’s most useful when schools have an embedded culture of being open to learning, sharing, and continually improving.
We found nine key practice areas that make a real difference
When we focus closely on what matters for maths teaching in particular, there are nine key areas of practice that make the difference for young maths students:
- teachers use their understanding of assessment and how students learn maths to ensure they all progress
- teachers use quality teaching practice in maths
- teachers provide dedicated maths time every day so all students engage meaningfully in learning
- teachers notice when students require extra support for learning and provide effective targeted teaching
- teachers use tools and representations to express mathematical concepts
- the classroom learning environment encourages mathematical thinking, collaboration, and the enjoyment of maths
- teachers make the most of moments throughout the day to highlight and use maths
- maths classes reflect the cultures of their students and their families/whānau
- teachers work in partnership with families/whānau to support maths learning.
Actions that prioritise maths add up
Great maths teaching starts with teachers valuing maths. When maths is prioritised, this is visible through teacher actions like dedicated daily maths time, weaving maths learning throughout other curriculum areas, purposeful use of maths talk, linking students’ interests and cultures back to maths ideas, and making great tools and materials available and well understood.
The practices and examples in this report show that great maths teaching doesn’t need to be complicated - but it does need to be grounded in a solid grasp of maths concepts and how maths learning works. The teachers and leaders who shared their stories with us valued hands-on, collaborative learning and lots of opportunities to unpack maths concepts with their peers. This is where they could really dig into what maths learning looks like and feels like for their students, and they came away energised.
When maths is a consistent and engaging feature of the everyday programme, students are steeped in rich and relevant experiences that help them to make connections, cement new learning, think and talk in maths terms, and explore maths ideas. This all starts with clear messages from teachers: that maths is important, maths connects to their world, maths is fun and interesting, and maths is for everyone.
Teachers can use this report to grow their practice
This report puts research evidence and real-life stories together to shine a light on the key ways that teachers can improve their maths teaching. The experiences that were shared with us, and the research evidence, affirm that great early maths teaching leads to great early maths outcomes - and more confident maths students going forward.
Years 1-3 are when crucial maths learning happens. Teachers have the chance in these years to provide students with the foundational maths understandings that set them up for success in their future schooling and beyond. This all starts with teachers valuing maths, and being grounded in a solid grasp of maths concepts and how maths learning works.
In this report, we put research and real-life stories together to shine a light on the key ways that teachers can improve their maths teaching, to benefit our young maths students.
Early maths really matters
In the early years of primary school, teachers have the opportunity to set the scene for their young maths students. It is in these early years that students form their foundational understandings of maths concepts, and of their own capability as maths students. We know that maths is the pathway to success in many other learning areas as well as having longer-term economic benefits, which means early maths has big impacts for learning and life outcomes.
However, not all students and teachers are confident about maths. Our national achievement picture isn’t strong, and not all teachers feel prepared for engaging students in this crucial area of their schooling.
This research uses robust evidence from the global and local research base, combined with real-life insights and strategies from Aotearoa New Zealand classrooms, to clarify ‘what good looks like’ in early maths teaching. By shining a light on good practice, we hope to inspire teachers to improve their maths teaching practice.
We found two key enablers that set teachers up to do their best work
Great maths teaching needs great foundations. Teachers need to be confident in their own maths knowledge and skills so that they are ready to teach them to their students. They also need to know about what works for young students: the evidence-based teaching and learning strategies that set up the key understandings needed for this part of their maths journey. This includes being clear about the best ways to build up important maths ideas, while avoiding misunderstandings or shortcuts which negatively impact on later learning.
Teachers’ school settings set the scene for good maths practice by promoting a clear, shared understanding of the value of quality maths teaching. Schools can do this by clearly setting out what maths teaching and maths progress look like in their whole school curriculum, and supporting teacher understanding with great learning and collaboration opportunities. It’s most useful when schools have an embedded culture of being open to learning, sharing, and continually improving.
We found nine key practice areas that make a real difference
When we focus closely on what matters for maths teaching in particular, there are nine key areas of practice that make the difference for young maths students:
- teachers use their understanding of assessment and how students learn maths to ensure they all progress
- teachers use quality teaching practice in maths
- teachers provide dedicated maths time every day so all students engage meaningfully in learning
- teachers notice when students require extra support for learning and provide effective targeted teaching
- teachers use tools and representations to express mathematical concepts
- the classroom learning environment encourages mathematical thinking, collaboration, and the enjoyment of maths
- teachers make the most of moments throughout the day to highlight and use maths
- maths classes reflect the cultures of their students and their families/whānau
- teachers work in partnership with families/whānau to support maths learning.
Actions that prioritise maths add up
Great maths teaching starts with teachers valuing maths. When maths is prioritised, this is visible through teacher actions like dedicated daily maths time, weaving maths learning throughout other curriculum areas, purposeful use of maths talk, linking students’ interests and cultures back to maths ideas, and making great tools and materials available and well understood.
The practices and examples in this report show that great maths teaching doesn’t need to be complicated - but it does need to be grounded in a solid grasp of maths concepts and how maths learning works. The teachers and leaders who shared their stories with us valued hands-on, collaborative learning and lots of opportunities to unpack maths concepts with their peers. This is where they could really dig into what maths learning looks like and feels like for their students, and they came away energised.
When maths is a consistent and engaging feature of the everyday programme, students are steeped in rich and relevant experiences that help them to make connections, cement new learning, think and talk in maths terms, and explore maths ideas. This all starts with clear messages from teachers: that maths is important, maths connects to their world, maths is fun and interesting, and maths is for everyone.
Teachers can use this report to grow their practice
This report puts research evidence and real-life stories together to shine a light on the key ways that teachers can improve their maths teaching. The experiences that were shared with us, and the research evidence, affirm that great early maths teaching leads to great early maths outcomes - and more confident maths students going forward.
Useful resources
There are many resources available for teachers interested in improving their teaching of maths in Years 1-3. Links and information about some of these resources are set out in the table below. Teachers will also find it useful to discuss resources and programmes with their syndicate, curriculum, or school leaders, or their regional Ministry of Education curriculum leads.
|
Link |
What’s it about? |
Who is it for? |
|
Making it Count: Teaching Maths in Years 1-3: Guide for Teachers
https://evidence.ero.govt.nz/documents/guide-for-teachers-teaching-maths-in-years-1-to-3 |
This guide for Year 1-3 teachers collates the key information from this report into a practical resource. It mainly focuses on material from Part 3 of this report.
|
Primary school teachers and leaders. It draws on research and real life stories to offer concise, practical strategies to effectively teach maths to students in Years 1 - 3. |
|
A practical guide for teachers: What quality teacher aide practice looks like https://evidence.ero.govt.nz/documents/a-practical-guide-for-teachers-what-quality-teacher-aide-practice-looks-like
|
This guide sets out what good teacher aide practice looks like, and practical actions for teachers to help make it happen. It includes a section on ‘delivering structured interventions’ which may be particularly useful for maths contexts. |
Primary school teachers who work alongside teacher aides in their maths programme. |
|
Tāhūrangi - New Zealand Curriculum https://newzealandcurriculum.tahurangi.education.govt.nz/ |
The new website for the New Zealand maths curriculum. This website will have a range of curriculum content, teaching materials, and news. Much of the extensive material and resources from the existing NZMaths website will move onto this site. |
Teachers and leaders looking for maths learning and teaching resources and professional learning material to support maths curriculum development and implementation. |
|
The Education Hub, NZ |
Useful guidance and consideration for improving teacher practice in maths. |
Supporting teachers to think about their maths practice and programmes. |
|
Teaching Primary School Mathematics and Statistics: Evidence-based practice. Averill, R., & Harvey, R. (2010). Teaching Primary School Mathematics and Statistics: Evidence-Based Practice. New Zealand Council for Educational Research. |
This book includes practical activities and consideration for teaching a wide range of content areas: number, algebra, geometry, measurement, statistics and probability. |
Teachers who want to look more deeply into aspects of their maths practice and find some practical ideas. |
|
Growth mindset - PLD session for schools https://newzealandcurriculum.tahurangi.education.govt.nz/5637190479.p |
A “mini-professional development session,” which includes readings, videos, and reflective questions. |
Teachers looking to grow their capability in workshop facilitation. |
|
Developing Mathematical Inquiry Communities (DMIC)
|
Developing Mathematical Inquiry Communities (DMIC) is a maths programme for primary schools focussed on structuring lessons to encourage students to work together to solve problems, and support all students to engage and feel successful. |
Leaders and teachers who want to encourage students to work collaboratively to solve problems that have culturally relevant contexts for students. |
|
SPRING into maths https://springintomaths.com/about/
|
SPRING offers six kits designed to support students to understand key number concepts. Each kit contains resources including lesson ideas, student progress charts, sample weekly plan. Before purchasing the ‘kits’ from the SPRING website, schools will need to pay for training. |
Teachers who want to try a new structured way to support their students to develop their maths skills. |
|
National Council of Teachers of Mathematics (NCTM) |
NCTM is a USA-based mathematics education organisation that offers a wide range of classroom resources and maths games. Some of these are free and others require membership before accessing them. |
Teachers who want to introduce more fun and challenging tasks to help their students practice maths skills and build their maths knowledge. |
|
14 teaching practices for enhancing learning |
The 14 teaching practices found on this website are designed to create an ideal classroom environment for learning maths. They can be found in his book Big thinking classrooms in mathematics. |
Teachers looking for ways to make their classroom environment more supportive of maths learning. |
|
Learning and Teaching with Learning Trajectories, Early Math - Birth to Grade 3 https://www.learningtrajectories.org/math/learning-trajectories |
Practical examples for teaching and learning about concepts within Number, Space, Measurement and statistics for young students. |
Helping teachers to better understand how to teach children different maths skills. |
There are many resources available for teachers interested in improving their teaching of maths in Years 1-3. Links and information about some of these resources are set out in the table below. Teachers will also find it useful to discuss resources and programmes with their syndicate, curriculum, or school leaders, or their regional Ministry of Education curriculum leads.
|
Link |
What’s it about? |
Who is it for? |
|
Making it Count: Teaching Maths in Years 1-3: Guide for Teachers
https://evidence.ero.govt.nz/documents/guide-for-teachers-teaching-maths-in-years-1-to-3 |
This guide for Year 1-3 teachers collates the key information from this report into a practical resource. It mainly focuses on material from Part 3 of this report.
|
Primary school teachers and leaders. It draws on research and real life stories to offer concise, practical strategies to effectively teach maths to students in Years 1 - 3. |
|
A practical guide for teachers: What quality teacher aide practice looks like https://evidence.ero.govt.nz/documents/a-practical-guide-for-teachers-what-quality-teacher-aide-practice-looks-like
|
This guide sets out what good teacher aide practice looks like, and practical actions for teachers to help make it happen. It includes a section on ‘delivering structured interventions’ which may be particularly useful for maths contexts. |
Primary school teachers who work alongside teacher aides in their maths programme. |
|
Tāhūrangi - New Zealand Curriculum https://newzealandcurriculum.tahurangi.education.govt.nz/ |
The new website for the New Zealand maths curriculum. This website will have a range of curriculum content, teaching materials, and news. Much of the extensive material and resources from the existing NZMaths website will move onto this site. |
Teachers and leaders looking for maths learning and teaching resources and professional learning material to support maths curriculum development and implementation. |
|
The Education Hub, NZ |
Useful guidance and consideration for improving teacher practice in maths. |
Supporting teachers to think about their maths practice and programmes. |
|
Teaching Primary School Mathematics and Statistics: Evidence-based practice. Averill, R., & Harvey, R. (2010). Teaching Primary School Mathematics and Statistics: Evidence-Based Practice. New Zealand Council for Educational Research. |
This book includes practical activities and consideration for teaching a wide range of content areas: number, algebra, geometry, measurement, statistics and probability. |
Teachers who want to look more deeply into aspects of their maths practice and find some practical ideas. |
|
Growth mindset - PLD session for schools https://newzealandcurriculum.tahurangi.education.govt.nz/5637190479.p |
A “mini-professional development session,” which includes readings, videos, and reflective questions. |
Teachers looking to grow their capability in workshop facilitation. |
|
Developing Mathematical Inquiry Communities (DMIC)
|
Developing Mathematical Inquiry Communities (DMIC) is a maths programme for primary schools focussed on structuring lessons to encourage students to work together to solve problems, and support all students to engage and feel successful. |
Leaders and teachers who want to encourage students to work collaboratively to solve problems that have culturally relevant contexts for students. |
|
SPRING into maths https://springintomaths.com/about/
|
SPRING offers six kits designed to support students to understand key number concepts. Each kit contains resources including lesson ideas, student progress charts, sample weekly plan. Before purchasing the ‘kits’ from the SPRING website, schools will need to pay for training. |
Teachers who want to try a new structured way to support their students to develop their maths skills. |
|
National Council of Teachers of Mathematics (NCTM) |
NCTM is a USA-based mathematics education organisation that offers a wide range of classroom resources and maths games. Some of these are free and others require membership before accessing them. |
Teachers who want to introduce more fun and challenging tasks to help their students practice maths skills and build their maths knowledge. |
|
14 teaching practices for enhancing learning |
The 14 teaching practices found on this website are designed to create an ideal classroom environment for learning maths. They can be found in his book Big thinking classrooms in mathematics. |
Teachers looking for ways to make their classroom environment more supportive of maths learning. |
|
Learning and Teaching with Learning Trajectories, Early Math - Birth to Grade 3 https://www.learningtrajectories.org/math/learning-trajectories |
Practical examples for teaching and learning about concepts within Number, Space, Measurement and statistics for young students. |
Helping teachers to better understand how to teach children different maths skills. |
Endnotes and References
- [1] Ministry of Education. (2022). Leading mathematics teaching and learning in years 1-8: What principals need to know and be able to do. Ministry of Education. https://nzcurriculum.tki.org.nz/content/download/169510/1250686/file/CO3072_Maths_Principals_011-web.pdf
- New Zealand Council of Educational Research. (2018). National monitoring study of student achievement 2018. Retrieved from https://shiny.nzcer.org.nz/nationalmonitoring/2018/
- Education Review Office. (2018). Teaching strategies that work - mathematics. Retrieved from https://ero.govt.nz/our-research/teaching-strategies-that-work-mathematics
- New Zealand Council for Educational Research. (2022). National monitoring study of student achievement 2022. Retrieved from https://nzcer.shinyapps.io/NMSSA2022/
- [1] Anthony, G., & Walshaw, M. (2007). Effective pedagogy in mathematics/pāngarau: Best Evidence Synthesis Iteration [BES]. Ministry of Education.
- Expert Advisory Panel. (2021). Pāngarau mathematics and tauanga statistics in Aotearoa New Zealand: Advice on refreshing the English-medium Mathematics and Statistics learning area of the New Zealand Curriculum. Royal Society Te Apārangi. Retrieved from https://www.royalsociety.org.nz/assets/Pangarau-Mathematics-and-Tauanga-Statistics-in-Aotearoa-New-Zealand-Digital.pdf
- [1] Ministry of Education (2022). Literacy & Communication and Maths Strategy. Retrieved from https://assets.education.govt.nz/public/Documents/Ministry/Changes-in-education/ELS-0778-Maths-and-Literacy-Strategies-Doc_web.pdf
- [1] Expert Advisory Panel. (2021). Pāngarau mathematics and tauanga statistics in Aotearoa New Zealand: Advice on refreshing the English-medium Mathematics and Statistics learning area of the New Zealand Curriculum. Royal Society Te Apārangi. Retrieved from https://www.royalsociety.org.nz/assets/Pangarau-Mathematics-and-Tauanga-Statistics-in-Aotearoa-New-Zealand-Digital.pdf
- [1] Ministry of Education. (2022). Leading mathematics teaching and learning in years 1-8: What principals need to know and be able to do. https://nzcurriculum.tki.org.nz/content/download/169510/1250686/file/CO3072_Maths_Principals_011-web.pdf
- [1] Gibbs, B., White, A., & McDowall, S. (2022). Developing a common practice model for literacy & communciation and maths: An overview of the literature. New Zealand Council for Educational Research.
- [1] Expert Advisory Panel. (2021). Pāngarau mathematics and tauanga statistics in Aotearoa New Zealand: Advice on refreshing the English-medium Mathematics and Statistics learning area of the New Zealand Curriculum. Royal Society Te Apārangi. Retrieved from https://www.royalsociety.org.nz/assets/Pangarau-Mathematics-and-Tauanga-Statistics-in-Aotearoa-New-Zealand-Digital.pdf
- [1] Parsons, S., & Bynner, J. (2005). Does numeracy matter more?. National Research and Development Centre for Adult Literacy and Numeracy
- [1] Expert Advisory Panel. (2021). Pāngarau mathematics and tauanga statistics in Aotearoa New Zealand: Advice on refreshing the English-medium Mathematics and Statistics learning area of the New Zealand Curriculum. Royal Society Te Apārangi. Retrieved from https://www.royalsociety.org.nz/assets/Pangarau-Mathematics-and-Tauanga-Statistics-in-Aotearoa-New-Zealand-Digital.pdf
- [1] Ministry of Education. (2022). What your child learns at early learning services. Retrieved from https://parents.education.govt.nz/early-learning/learning-at-an-ece-service/what-your-child-learns-at-ece/#whatwilltheylearn
- The Education Hub. (2020). An introduction to supporting early maths in early childhood education. Retrieved from https://theeducationhub.org.nz/an-introduction-to-supporting-early-maths-in-ece/#:~:text=They%20explore%20maths%20on%20their,arithmetic%20with%20groups%20of%20objects.
- [1] Education Review Office. (2016). Early mathematics: A guide for improving teaching and learning. New Zealand Government. Retrieved from https://ero.govt.nz/our-research/early-mathematics-a-guide-for-improving-teaching-and-learning
- [1] Ell, F., & Darragh, L. (n.d.). Teaching and learning mathematics at primary school. Retrieved from The Education Hub: https://theeducationhub.org.nz/teaching-and-learning-mathematics-at-primary-school/
- [1] Education Review Office. (2016). Early Mathematics: A guide for improving teaching and learning. New Zealand Government. Retrieved from https://ero.govt.nz/our-research/early-mathematics-a-guide-for-improving-teaching-and-learning
- Ell, F., & Darragh, L. (n.d.). Teaching and learning mathematics at primary school. Retrieved from The Education Hub: https://theeducationhub.org.nz/teaching-and-learning-mathematics-at-primary-school/
- [1] Holenstein, M., Bruckmaier, G. & Grob, A. (2021). Transfer effects of mathematical literacy: an integrative longitudinal study. European Journal of Psychology of Education, 36(9), 799–825. https://doi.org/10.1007/s10212-020-00491-4
- [1] Mohyuddin, R. G., & Khalil, U. (2016). Misconceptions of Students in Learning Mathematics at Primary Level. Bulletin of Education and Research, 38(1), 133-162.Fujii, T. (2020).
- Misconceptions and alternative conceptions in mathematics education. Encyclopedia of mathematics education, 625-627.
- [1] Gibbs, B., White, A., & McDowall, S. (2022). Developing a common practice model for literacy & communciation and maths: An overview of the literature. New Zealand Council for Educational Research.
- [1] Ministry of Education. (2022). Which angle is a right angle? Year 5 students’ strengths and weaknesses on mathematics questions. Retrieved from https://www.educationcounts.govt.nz/__data/assets/pdf_file/0003/213186/Which-angle-is-a-right-angle-Year-5-students-strengths-and-weaknesses-on-mathematics-questions.pdf
- [1] Ministry of Education. (2022). Which angle is a right angle? Year 5 students’ strengths and weaknesses on mathematics questions. Retrieved from https://www.educationcounts.govt.nz/__data/assets/pdf_file/0003/213186/Which-angle-is-a-right-angle-Year-5-students-strengths-and-weaknesses-on-mathematics-questions.pdf
- [1] OECD. (2023). PISA 2022 results: The state of learning and equality in education. Retrieved from https://read.oecd-ilibrary.org/view/?ref=1235_1235421-gumq51fbgo&title=PISA-2022-Results-Volume-I
- [1] Ministry of Education. (2023). PISA 2022 Mathematics Achievement and Experiences of 15-year-olds, by Emma Medina. Retrieved from https://www.educationcounts.govt.nz/__data/assets/pdf_file/0005/224609/PISA-2022_Mathematics-Achievement-and-Experiences-Report.pdf
- OECD. (2023). PISA 2022 results: The state of learning and equality in education. Retrieved from https://read.oecd-ilibrary.org/view/?ref=1235_1235421-gumq51fbgo&title=PISA-2022-Results-Volume-I
- OECD. (2023). PISA 2022 results. Retrieved from https://www.oecd.org/publication/pisa-2022-results/
- [1] National Monitoring Study of Student Achievement. (2022). Achievement in mathematics and statistics at year 4 and year 8: Findings from the 2022 National Monitoring Study of Student Achievement (NMSSA). Retrieved from https://nmssa-production.s3.amazonaws.com/documents/A3_NMSSA_2022_Achievement_Summary_Mathematics.pdf
- Ministry of Education. (2018). Achievement and progress in mathematics, reading and writing in primary schooling: Analysis of e-asTTle assessment data, 2011 to 2016. Retrieved from https://www.educationcounts.govt.nz/__data/assets/pdf_file/0019/185023/20171213-Achievement-and-Progress-in-mathematics-reading-and-writing.pdf
- [1] National Monitoring Study of Student Achievement. (2022). Achievement in mathematics and statistics at year 4 and year 8: Findings from the 2022 National Monitoring Study of Student Achievement (NMSSA). Retrieved from https://nmssa-production.s3.amazonaws.com/documents/A3_NMSSA_2022_Achievement_Summary_Mathematics.pdf
- [1] National Monitoring Study of Student Achievement. (2022). Achievement in mathematics and statistics at year 4 and year 8: Findings from the 2022 National Monitoring Study of Student Achievement (NMSSA). Retrieved from https://nmssa-production.s3.amazonaws.com/documents/A3_NMSSA_2022_Achievement_Summary_Mathematics.pdf
- [1] Medina, E. (2023). PISA 2022: Mathematics achievement and experiences of 15-year-olds. Retrieved from https://www.educationcounts.govt.nz/__data/assets/pdf_file/0005/224609/PISA-2022_Mathematics-Achievement-and-Experiences-Report.pdf
- [1] Education Review Office. (2022). Ongoing research on new teachers (forthcoming publication).
- [1] National Monitoring Study of Student Achievement. (2023). Mathematics and statistics: contextual findings 2022. Retrieved from https://nmssa-production.s3.amazonaws.com/documents/NMSSA_2022_Mathematics_Contextual_Findings.pdf
- [1] Expert Advisory Panel. (2021). Pāngarau mathematics and tauanga statistics in Aotearoa New Zealand: Advice on refreshing the English-medium Mathematics and Statistics learning area of the New Zealand Curriculum. Royal Society Te Apārangi. Retrieved from https://www.royalsociety.org.nz/assets/Pangarau-Mathematics-and-Tauanga-Statistics-in-Aotearoa-New-Zealand-Digital.pdf
- [1] Anderson, R., Boaler, J., & Dieckmann, J. (2018). Achieving Elusive Teacher Change through Challenging Myths about Learning: A Blended Approach. Education Sciences, 8(3), 98. MDPI AG. Retrieved from http://dx.doi.org/10.3390/educsci8030098
- [1] Anderson, R., Boaler, J., & Dieckmann, J. (2018). Achieving Elusive Teacher Change through Challenging Myths about Learning: A Blended Approach. Education Sciences, 8(3), 98. MDPI AG. Retrieved from http://dx.doi.org/10.3390/educsci8030098
- [1] Expert Advisory Panel. (2021). Pāngarau mathematics and tauanga statistics in Aotearoa New Zealand: Advice on refreshing the English-medium Mathematics and Statistics learning area of the New Zealand Curriculum. Royal Society Te Apārangi. Retrieved from https://www.royalsociety.org.nz/assets/Pangarau-Mathematics-and-Tauanga-Statistics-in-Aotearoa-New-Zealand-Digital.pdf
- [1] Anthony, G., & Walshaw, M. (2007). Effective Pedagogy in Mathematics/Pāngarau. Ministry of Education.
- [1] Ministry of Education. (n.d.). Local curriculum: Designing rich opportunities and coherent pathways for all students. Retrieved from https://nzcurriculum.tki.org.nz/Strengthening-local-curriculum/Leading-local-curriculum-guide-series/Local-curriculum
- [1] Anthony, G., & Walshaw, M. (2007). Effective Pedagogy in Mathematics/Pāngarau. Ministry of Education.
- Mohyuddin, R. G., & Khalil, U. (2016). Misconceptions of Students in Learning Mathematics at Primary Level. Bulletin of Education and Research, 38(1), 133-162.
- Fujii, T. (2020). Misconceptions and alternative conceptions in mathematics education. Encyclopedia of mathematics education, 625-627.
- Anderson, D. and Pritchard, R. (2010). Bridging the gap: Challenging conceptions of fractions and decimals. In Teaching Primary School Mathematics and Statistics, Eds. R. Averill & R. Harvey. NZCER Press: Wellington.
- [1] Clark, A., Henderson, P., & Gifford, S. (2020). Improving mathematics in the early years and key stage 1. Education Endowment Foundation. Retrieved from https://d2tic4wvo1iusb.cloudfront.net/production/eef-guidance-reports/early-maths/EEF_Maths_EY_KS1_Guidance_Report.pdf?v=1699919581
- [1] Expert Advisory Panel. (2021). Pāngarau mathematics and tauanga statistics in Aotearoa New Zealand: Advice on refreshing the English-medium Mathematics and Statistics learning area of the New Zealand Curriculum. Royal Society Te Apārangi. Retrieved from https://www.royalsociety.org.nz/assets/Pangarau-Mathematics-and-Tauanga-Statistics-in-Aotearoa-New-Zealand-Digital.pdf
- [1] Clark, A., Henderson, P., & Gifford, S. (2020). Improving mathematics in the early years and key stage 1. Education Endowment Foundation. Retrieved from https://d2tic4wvo1iusb.cloudfront.net/production/eef-guidance-reports/early-maths/EEF_Maths_EY_KS1_Guidance_Report.pdf?v=1699919581
- Dweck, C. S. (2006). Mindset: The new psychology of success. Random house.
- [1] Ministry of Education. (n.d.). Local curriculum: Designing rich opportunities and coherent pathways for all students. Retrieved from https://nzcurriculum.tki.org.nz/Strengthening-local-curriculum/Leading-local-curriculum-guide-series/Local-curriculum
- [1] Clark, A., Henderson, P., & Gifford, S. (2020). Improving mathematics in the early years and key stage 1. Education Endowment Foundation. Retrieved from https://d2tic4wvo1iusb.cloudfront.net/production/eef-guidance-reports/early-maths/EEF_Maths_EY_KS1_Guidance_Report.pdf?v=1699919581
- [1] Clark, A., Henderson, P., & Gifford, S. (2020). Improving mathematics in the early years and key stage 1. Education Endowment Foundation. Retrieved from https://d2tic4wvo1iusb.cloudfront.net/production/eef-guidance-reports/early-maths/EEF_Maths_EY_KS1_Guidance_Report.pdf?v=1699919581
- [1] Ministry of Education. (2023). A model of educational leadership. Retrieved from https://www.educationalleaders.govt.nz/Leadership-development/Key-leadership-documents/Kiwi-leadership-for-principals/A-model-of-educational-leadership
- [1] Hattie, J. (2016, July). Mindframes and Maximizers. 3rd Annual Visible Learning Conference held in Washington, DC
- Donohoo, J., Hattie, J., & Eells, R. (2018). The power of collective efficacy. Educational Leadership, 75(6), 40-44.
- [1] Ministry of Education. (n.d.). Ka Hikitia – Ka Hāpaitia. Retrieved from https://www.education.govt.nz/our-work/overall-strategies-and-policies/ka-hikitia-ka-hapaitia/
- Ministry of Education. (2023). Action plan for Pacific education 2020-2030: 2023 refresh. Retrieved from https://www.education.govt.nz/our-work/overall-strategies-and-policies/action-plan-for-pacific-education/
- [1] Kaskens, J., Segers, E., Goei, S. L., van Luit, J. E., & Verhoeven, L. (2020). Impact of Children’s math self-concept, math self-efficacy, math anxiety, and teacher competencies on math development. Teaching and teacher education, 94, 103096.
- Beswick, K. (2019). The role of knowledge and beliefs in helping students to progress their mathematical understanding. J Math Teacher Educ 22, 125–128
- [1] Flint, A., Garrett, L., McDonald, L., Rubie-Davies, C. M., & Watson, P. W. (2018). December 10). Viewing students consistently: how stable are teachers’ expectations? Educational Research and Evaluation, 24(3-5), 221-240.
- Philipp, R. A. (2007). Mathematics teachers' beliefs and affect. In F. K. Lester (ed.), Second handbook of research on mathematics teaching and learning (pp. 257–315). Charlotte: NCTM/Information Age Publishing
- Rubie-Davies, C. M., & Peterson, E. R. (2016). Relations between teachers’ over - and underestimation, and students' beliefs for Māori & Pākeha students.. Contemporary Educational Psychology, 47, 72-83.
- Hollenstein, L., Rubie-Davies, C. M., & Brühwiler, C. (2023). Teacher expectations and their relations with primary school students’ achievement, self-concept, and anxiety in mathematics. Social Psychology of Education, 1-20.
- [1] Kaskens, J., Segers, E., Goei, S. L., van Luit, J. E., & Verhoeven, L. (2020). Impact of Children’s math self-concept, math self-efficacy, math anxiety, and teacher competencies on math development. Teaching and teacher education, 94, 103096.
- Clark, A., Henderson, P., & Gifford, S. (2020). Improving mathematics in the early years and key stage 1. Education Endowment Foundation. Retrieved from https://d2tic4wvo1iusb.cloudfront.net/production/eef-guidance-reports/early-maths/EEF_Maths_EY_KS1_Guidance_Report.pdf?v=1699919581
- [1] Clark, A., Henderson, P., & Gifford, S. (2020). Improving mathematics in the early years and key stage 1. Education Endowment Foundation. Retrieved from https://d2tic4wvo1iusb.cloudfront.net/production/eef-guidance-reports/early-maths/EEF_Maths_EY_KS1_Guidance_Report.pdf?v=1699919581
- [1] Clark, A., Henderson, P., & Gifford, S. (2020). Improving mathematics in the early years and key stage 1. Education Endowment Foundation. Retrieved from https://d2tic4wvo1iusb.cloudfront.net/production/eef-guidance-reports/early-maths/EEF_Maths_EY_KS1_Guidance_Report.pdf?v=1699919581
- [1] Anthony, G., & Walshaw, M. (2007). Effective pedagogy in mathematics/pāngarau: Best Evidence Synthesis Iteration [BES]. Ministry of Education.
- [1] National Council of Teachers of Mathematics. (2023). Procedural Fluency in Mathematics. Retrieved from https://www.nctm.org/Standards-and-Positions/Position-Statements/Procedural-Fluency-in-Mathematics/
- [1] Doabler, C. T., Cary, M. S., Jungjohann, K., Clarke, B., Fien, H., Baker, S., & Chard, D. (2012). Enhancing core mathematics instruction for students at risk for mathematics disabilities. Teaching Exceptional Children, 44(4), 48-57.
- [1] Wang, A. H., Firmender, J. M., Power, J. R., & Byrnes, J. P. (2016). Understanding the Program Effectiveness of Early Mathematics Interventions for Prekindergarten and Kindergarten Environments: A Meta-Analytic Review. Early Education and Development, 27(5), 692–713. https://doi.org/10.1080/10409289.2016.1116343
- [1] Wright, J. Intervention Central. (n.d.). Math Problem-Solving: Combining Cognitive & Metacognitive Strategies. Retrieved from https://www.interventioncentral.org/academic-interventions/math/math-problem-solving-combining-cognitive-metacognitive-strategies
- [1] Clark, A., Henderson, P., & Gifford, S. (2020). Improving mathematics in the early years and key stage 1. Education Endowment Foundation. Retrieved from https://d2tic4wvo1iusb.cloudfront.net/production/eef-guidance-reports/early-maths/EEF_Maths_EY_KS1_Guidance_Report.pdf?v=1699919581
- [1] Expert Advisory Panel. (2021). Pāngarau mathematics and tauanga statistics in Aotearoa New Zealand: Advice on refreshing the English-medium Mathematics and Statistics learning area of the New Zealand Curriculum. Royal Society Te Apārangi. Retrieved from https://www.royalsociety.org.nz/assets/Pangarau-Mathematics-and-Tauanga-Statistics-in-Aotearoa-New-Zealand-Digital.pdf
- [1] O'Neill, S., Gillic, C., & Kingston, M. (2023). Pedagogical strategies, approaches and methodologies to support numeracy in early childhood A review of the literature.
- [1] National Council of Teachers of Mathematics. (2023). Procedural Fluency Reasoning and Decision-Making, Not Rote Application of Procedures Position. Retrieved from https://www.nctm.org/Standards-and-Positions/Position-Statements/Procedural-Fluency-in-Mathematics/
- [1] NRICH team. (2019). Low Threshold High Ceiling - an Introduction. Retrieved from https://nzcurriculum.tki.org.nz/content/download/169510/1250686/file/CO3072_Maths_Principals_011-web.pdf
- Sullivan, P., Bragg, L. A. (Ed.), Cheeseman, J., Michels, D., Mornane, A., Clarke, D., Middleton, J., & Roche, A. (2011). Challenging mathematics tasks: What they are and how to use them. 33-46.
- Grootenboer, P. (2009). Rich mathematical tasks in the Maths in the Kimberley (MITK) Project. 696-699.
- [1] Ministry of Education. (2022). Leading mathematics teaching and learning in years 1-8: What principals need to know and be able to do. file:///C:/Users/ruthp/AppData/Local/Temp/MicrosoftEdgeDownloads/4761cd9b-f999-4f7c-9b4e-896b2751195e/CO3072_Maths_Principals_011-web.pdf
- [1] NRICH team. (2019). Low Threshold High Ceiling - an Introduction. Retrieved from https://nrich.maths.org/10345
- [1] Gervasoni, A., & Lindenskov, L. (2011). Students with ‘special rights’ for mathematics education. Mapping equity and quality in mathematics education, 307-323.
- [1] Anthony, G., & Walshaw, M. (2007). Effective Pedagogy in Mathematics/Pāngarau. Ministry of Education.
- Beyers, J. (2011). Student dispositions with respect to mathematics: What current literature says. Motivation and disposition: Pathways to learning mathematics, 69-79.
- OECD. (2013). Mathematics self-beliefs and participation in mathematics-related activities. PISA2012-Vol3-Chap4.pdf (oecd.org)
- OECD. (2013). PISA 2012 Results: Ready to Learn (Volume III): Students' Engagement, Drive and Self-Beliefs. Paris: PISA, OECD Publishing. Retrieved from https://doi.org/10.1787/19963777
- OECD. (2016). Opportunity to Learn and Students' Attitudes Towards Mathematics. In Equations and Inequalities: Making Mathematics Accessible to All. Paris: OECD Publishing. doi: https://doi.org/10.1787/9789264258495-7-en
- [1] Mielicki, M. K., Schiller, L. K., Fitzsimmons, C. J., Scheibe, D., & Thompson, C. A. (2022). Perceptions of ease and difficulty, but not growth mindset, relate to specific math attitudes. British Journal of Educational Psychology, 92(2), 707-729.
- [1] NRICH team. (2019). Low Threshold High Ceiling - an Introduction. Retrieved from https://nrich.maths.org/10345
- Livy, S., Muir, T., & Sullivan, P. (2018). Challenging tasks lead to productive struggle!. Australian Primary Mathematics Classroom, 23(1), 19-24.
- [1] Hattie, J. (2016, July). Mindframes and Maximizers. 3rd Annual Visible Learning Conference held in Washington, DC
- [1] Dweck, C. S. (2006). Mindset: The new psychology of success. Random house.
- [1] Sullivan, P., Cheeseman, J., Michels, D., Mornane, A., Clarke, D., Roche, A., & Middleton, J. (2011). Challenging mathematics tasks: What they are and how to use them. Maths is multi-dimensional, 33-46.
- Sullivan, P. (2017). Challenging mathematics tasks: What they are and how to use them.
- [1] Clark, A., Henderson, P., & Gifford, S. (2020). Improving mathematics in the early years and key stage 1. Education Endowment Foundation. Retrieved from https://d2tic4wvo1iusb.cloudfront.net/production/eef-guidance-reports/early-maths/EEF_Maths_EY_KS1_Guidance_Report.pdf?v=1699919581
- [1] Clark, A., Henderson, P., & Gifford, S. (2020). Improving mathematics in the early years and key stage 1. Education Endowment Foundation. Retrieved from https://d2tic4wvo1iusb.cloudfront.net/production/eef-guidance-reports/early-maths/EEF_Maths_EY_KS1_Guidance_Report.pdf?v=1699919581
- [1] Education Review Office. (2022). A practical guide for teachers: What quality teacher aide practice looks like. Retrieved from https://ero.govt.nz/our-research/a-practical-guide-for-teachers-what-quality-teacher-aide-practice-looks-like
- [1] Ministry of Education. (n.d.). Accelerating learning in mathematics fact sheet. Te Kete Ipurangi.
- [1] Ministry of Education. (2012). Resource 8: Creating purposeful independent activitiesl. Retrieved from https://nzmaths.co.nz/sites/default/files/images/ALiM_Resource08.pdf
- [1] nzmaths. (n.d.). ALiM resources. Retrieved from Te Kete Ipurangi: https://nzmaths.co.nz/alim-resources
- [1] Diezmann, C., & Watters, J., 1997, as cited in Anthony, G., & Walshaw, M. (2007). Effective pedagogy in mathematics/pāngarau: Best Evidence Synthesis Iteration [BES]. Ministry of Education.
- [1] Kusmaryono, I. (2014). The importance of mathematical power in mathematics learning. In International Conference on Mathematics, Science, and Education (Vol. 2014, pp. 35-40).
- [1] Sullivan, P., Bragg, L. A. (Ed.), Cheeseman, J., Michels, D., Mornane, A., Clarke, D., Middleton, J., & Roche, A. (2011). Challenging mathematics tasks: What they are and how to use them. 33-46.
- [1] Diezmann, C., & Watters, J., 1997, as cited in Anthony, G., & Walshaw, M. (2007). Effective pedagogy in mathematics/pāngarau: Best Evidence Synthesis Iteration [BES]. Ministry of Education.
- Mendes, I. A., & da Silva, C. A. (2018). Problematization and research as a method of teaching mathematics. International Electronic Journal of Mathematics Education, 13(2), 41-55. Retrieved from https://www.iejme.com/download/problematization-and-research-as-a-method-of-teaching-mathematics.pdf
- Mathematics Hub. (n.d.). Mathematics investigation. Retrieved from https://www.mathematicshub.edu.au/plan-teach-and-assess/teaching/teaching-strategies/mathematics-investigation/
- [1] Clark, A., Henderson, P., & Gifford, S. (2020). Improving mathematics in the early years and key stage 1. Education Endowment Foundation. Retrieved from https://d2tic4wvo1iusb.cloudfront.net/production/eef-guidance-reports/early-maths/EEF_Maths_EY_KS1_Guidance_Report.pdf?v=1699919581
- Mueller, M., Yankelewitz, D., & Maher, C. (2014). Teachers promoting student mathematical reasoning. Investigations in Mathematics Learning, 7(2). Retrieved from https://files.eric.ed.gov/fulltext/EJ1052941.pdf
- [1] Clark, A., Henderson, P., & Gifford, S. (2020). Improving mathematics in the early years and key stage 1. Education Endowment Foundation. Retrieved from https://d2tic4wvo1iusb.cloudfront.net/production/eef-guidance-reports/early-maths/EEF_Maths_EY_KS1_Guidance_Report.pdf?v=1699919581
- [1] Anthony, G., & Walshaw, M. (2009). Effective pedagogy in mathematics. International Academy of Education, 19, 136. Retrieved from https://nzmaths.co.nz/sites/default/files/images/EdPractices_19.pdf
- [1] Clark, A., Henderson, P., & Gifford, S. (2020). Improving mathematics in the early years and key stage 1. Education Endowment Foundation. Retrieved from https://d2tic4wvo1iusb.cloudfront.net/production/eef-guidance-reports/early-maths/EEF_Maths_EY_KS1_Guidance_Report.pdf?v=1699919581
- [1] Clements, D. H., & Sarama, J. (2016). Math, Science, and Technology in the Early Grades. The Future of Children, 26(2), 75–94. Retrieved from http://www.jstor.org/stable/43940582
- [1] Clark, A., Henderson, P., & Gifford, S. (2020). Improving mathematics in the early years and key stage 1. Education Endowment Foundation. Retrieved from https://d2tic4wvo1iusb.cloudfront.net/production/eef-guidance-reports/early-maths/EEF_Maths_EY_KS1_Guidance_Report.pdf?v=1699919581
- [1] OECD. (2016). Opportunity to Learn and Students' Attitudes Towards Mathematics. In Equations and Inequalities: Making Mathematics Accessible to All. Paris: OECD Publishing. doi:https://doi.org/10.1787/9789264258495-7-en
- Anthony, G., & Walshaw, M. (2007). Effective pedagogy in mathematics/pāngarau: Best Evidence Synthesis Iteration [BES]. Ministry of Education.
- Bonne, L. (2016). New Zealand Students’ mathematics-related beliefs and attitudes: recent evidence. N.Z.J. Educ. Stud. 51, 69–82. doi: 10.1007/s40841-016-0035-2
- [1] Stein, C. A. (2007). Let's talk: Promoting mathematical discourse in the classroom. The Mathematics Teacher, 101(4), 285-289.
- Goos, M., & Kaya, S. (2020). Understanding and promoting students’ mathematical thinking: a review of research published in ESM. Educational Studies in Mathematics, 103(1), 7-25.
- Anthony, G., & Walshaw, M. (2007). Effective pedagogy in mathematics/pāngarau: Best Evidence Synthesis Iteration [BES]. Ministry of Education.
- [1] Anthony, G., & Walshaw, M. (2007). Effective pedagogy in mathematics/pāngarau: Best Evidence Synthesis Iteration [BES]. Ministry of Education.
- Clark, A., Henderson, P., & Gifford, S. (2020). Improving mathematics in the early years and key stage 1. Education Endowment Foundation. Retrieved from https://d2tic4wvo1iusb.cloudfront.net/production/eef-guidance-reports/early-maths/EEF_Maths_EY_KS1_Guidance_Report.pdf?v=1699919581
- [1] Stein, C. A. (2007). Let's talk: Promoting mathematical discourse in the classroom. The Mathematics Teacher, 101(4), 285-289.
- Way, J. & Bobis, J. (2017). The Literacy of Mathematics. PETAA – Primary English Teaching Association Australia, 208, 1-12.
- [1] Anthony, G & Walshaw, M. (2009). Effective Pedagogy in Mathematics/Pāngarau BES
- Nzmaths (n.d.). Foster a supportive learning environment.
- Retrieved from: https://nzmaths.co.nz/foster-supportive-learning-environment
- [1] Anderson, D., Averill, R., Te Maro, P., Taiwhati, M., & Higgins, J. (2010). Knowing each other as students: Māori students learning mathematics. Delving into diversity: An international exploration of issues of diversity in education, 45-56.
- [1] Anthony, G., & Walshaw, M. (2007). Creating opportunities for learning with mathematical tasks. Set: Research Information for Teachers(1), 7-11. doi:10.18296/set.0547
- [1] Clark, A., Henderson, P., & Gifford, S. (2020). Improving mathematics in the early years and key stage 1. Education Endowment Foundation. Retrieved from https://d2tic4wvo1iusb.cloudfront.net/production/eef-guidance-reports/early-maths/EEF_Maths_EY_KS1_Guidance_Report.pdf?v=1699919581
- [1] Charles, R. I., & Carmel, C. A. (2005). Big ideas and understandings as the foundation for elementary and middle school mathematics. Journal of Mathematics Education, 7(3), 9-24.
- McDowell, S., & Hipkins, R. (n.d.). Cultural integration: what is happening in New Zealand schools? New Zealand Council for Educational Research. Retrieved from https://www.nzcer.org.nz/system/files/Curriculum%20Integration%202018-2019.pdf
- [1] Anthony, G., & Walshaw, M. (2007). Creating opportunities for learning with mathematical tasks. Set: Research Information for Teachers(1), 7-11. doi:10.18296/set.0547
- [1] De Holton, D., Ahmed, A., Williams, H., & Hill, C. (2001). On the importance of mathematical play. International Journal of Mathematical Education in Science and Technology, 32(3), 401-415.
- Hanline, M. F., Milton, S., & Phelps, P. C. (2010). The relationship between preschool block play and reading and maths abilities in early elementary school: A longitudinal study of children with and without disabilities. Early Child Development and Care, 180(8), 1005-1017.
- [1] Clark, A., Henderson, P., & Gifford, S. (2020). Improving mathematics in the early years and key stage 1. Education Endowment Foundation. Retrieved from https://d2tic4wvo1iusb.cloudfront.net/production/eef-guidance-reports/early-maths/EEF_Maths_EY_KS1_Guidance_Report.pdf?v=1699919581
- [1] Ministry of Education. (2022). Leading mathematics teaching and learning in years 1-8: What principals need to know and be able to do. https://nzcurriculum.tki.org.nz/content/download/169510/1250686/file/CO3072_Maths_Principals_011-web.pdf
- [1] Education Review Office. (2023). Education For All Our Children: Embracing Diverse Ethnicities. Retrieved from https://ero.govt.nz/our-research/education-for-all-our-children-embracing-diverse-ethnicities
- [1] OECD. (2016). Equations and Inequalities: Making Mathematics Accessible to All. Retrieved from https://www.oecd-ilibrary.org/education/equations-and-inequalities_9789264258495-en
- [1] Education Council. (n.d.). Our code our standards: code of professional responsibility and standards for the teaching profession. Retrieved from https://teachingcouncil.nz/assets/Files/Code-and-Standards/Our-Code-Our-Standards-Nga-Tikanga-Matatika-Nga-Paerewa.pdf
- Ministry of Education. (2015). The New Zealand Curriculum for English-medium teaching and learning in years 1-13. Wellington.
- Ministry of Education. (n.d.). Ka Hikitia – Ka Hāpaitia. Retrieved from https://www.education.govt.nz/our-work/overall-strategies-and-policies/ka-hikitia-ka-hapaitia/
- Ministry of Education. (2022). Literacy & communication and maths strategy. Retrieved from https://assets.education.govt.nz/public/Documents/Ministry/Changes-in-education/ELS-0778-Maths-and-Literacy-Strategies-Doc_web.pdf
- [1] Averill, R., Anderson, D., Easton, H., Te Maro, P., Smith, D., & Hynds, A. (2009). Culturally Responsive Teaching of Mathematics: Three Models from Linked Studies. Journal for Research in Mathematics Education, 40(2), 157-186. Retrieved from https://www.jstor.org/stable/40539330
- [1] Hunter, Jodie. (n.d.). Ambitious mathematics for young Pacific students: Dr Jodie Hunter demonstrates algebraic thinking for tivaevae. Retrieved from Education Counts: https://www.educationcounts.govt.nz/topics/bes/ambitious-mathematics-for-young-pacific-students
- Barnes, G. (2023, June 3). My Tūrangawaewae. Retrieved from https://instructionalseries.tki.org.nz/Instructional-Series/School-Journal/School-Journal-Level-2-June-2023/My-Turangawaewae
- [1] Te Poutāhū. (n.d.). Pattern Makers. Retrieved from https://newzealandcurriculum.tahurangi.education.govt.nz/pattern-makers/5637186629.p
- [1] Hunter, Jodie. (n.d.). Ambitious mathematics for young Pacific students: Dr Jodie Hunter demonstrates algebraic thinking for tivaevae. Retrieved from Education Counts: https://www.educationcounts.govt.nz/topics/bes/ambitious-mathematics-for-young-pacific-students
- Barnes, G. (2023, June 3). My Tūrangawaewae. Retrieved from https://instructionalseries.tki.org.nz/Instructional-Series/School-Journal/School-Journal-Level-2-June-2023/My-Turangawaewae
- [1] Education Review Office. (2015). Educationally powerful connections with parents and whānau. Retrieved from https://ero.govt.nz/our-research/educationally-powerful-connections-with-parents-and-whanau
- Ministry of Education (n.d). Partnering with parents, whānau, and communities. Retrieved from https://inclusive.tki.org.nz/guides/partnering-with-parents-whanau-and-communities/
- The Education Hub. (2020). What is parent partnership? Retrieved from https://theeducationhub.org.nz/what-is-parent-partnership/
- Anthony, G., & Walshaw, M. (2007). Effective pedagogy in mathematics/pāngarau: Best Evidence Synthesis Iteration [BES]. Ministry of Education.
- [1] Stanford Graduate School of Education. (n.d.). Parents’ beliefs about math change their children’s achievement. Retrieved from youcubed: https://www.youcubed.org/evidence/parents-beliefs-math-change-childrens-achievement/
- [1] O'Neill, S., Gillic, C., & Kingston, M. (2023). Pedagogical strategies, approaches and methodologies to support numeracy in early childhood A review of the literature.
- [1] Stanford Graduate School of Education. (n.d.). Parents’ beliefs about math change their children’s achievement. Retrieved from youcubed: https://www.youcubed.org/evidence/parents-beliefs-math-change-childrens-achievement/
- [1] Farr, S. (2015). The role of parents in children's attitudes towards mathematics. Retrieved from https://researchcommons.waikato.ac.nz/bitstream/handle/10289/10007/thesis.pdf?sequence=3&isAllowed=y
- [1] nzmaths. (n.d.). Guiding beliefs. Retrieved from Te Kete Ipurangi: https://nzmaths.co.nz/guiding-beliefs
- [1] Papadopoulos, I. (2017). Opening inquiry mathematics to parents: Can they be engaged as teachers’ partners in mathematical work? Journal of Pedagogical Research, 1(1), 1-20.
- [1] Ministry of Education. (2022). Leading mathematics teaching and learning in years 1-8: What principals need to know and be able to do. Ministry of Education. https://nzcurriculum.tki.org.nz/content/download/169510/1250686/file/CO3072_Maths_Principals_011-web.pdf
- New Zealand Council of Educational Research. (2018). National monitoring study of student achievement 2018. Retrieved from https://shiny.nzcer.org.nz/nationalmonitoring/2018/
- Education Review Office. (2018). Teaching strategies that work - mathematics. Retrieved from https://ero.govt.nz/our-research/teaching-strategies-that-work-mathematics
- New Zealand Council for Educational Research. (2022). National monitoring study of student achievement 2022. Retrieved from https://nzcer.shinyapps.io/NMSSA2022/
- [1] Anthony, G., & Walshaw, M. (2007). Effective pedagogy in mathematics/pāngarau: Best Evidence Synthesis Iteration [BES]. Ministry of Education.
- Expert Advisory Panel. (2021). Pāngarau mathematics and tauanga statistics in Aotearoa New Zealand: Advice on refreshing the English-medium Mathematics and Statistics learning area of the New Zealand Curriculum. Royal Society Te Apārangi. Retrieved from https://www.royalsociety.org.nz/assets/Pangarau-Mathematics-and-Tauanga-Statistics-in-Aotearoa-New-Zealand-Digital.pdf
- [1] Ministry of Education (2022). Literacy & Communication and Maths Strategy. Retrieved from https://assets.education.govt.nz/public/Documents/Ministry/Changes-in-education/ELS-0778-Maths-and-Literacy-Strategies-Doc_web.pdf
- [1] Expert Advisory Panel. (2021). Pāngarau mathematics and tauanga statistics in Aotearoa New Zealand: Advice on refreshing the English-medium Mathematics and Statistics learning area of the New Zealand Curriculum. Royal Society Te Apārangi. Retrieved from https://www.royalsociety.org.nz/assets/Pangarau-Mathematics-and-Tauanga-Statistics-in-Aotearoa-New-Zealand-Digital.pdf
- [1] Ministry of Education. (2022). Leading mathematics teaching and learning in years 1-8: What principals need to know and be able to do. https://nzcurriculum.tki.org.nz/content/download/169510/1250686/file/CO3072_Maths_Principals_011-web.pdf
- [1] Gibbs, B., White, A., & McDowall, S. (2022). Developing a common practice model for literacy & communciation and maths: An overview of the literature. New Zealand Council for Educational Research.
- [1] Expert Advisory Panel. (2021). Pāngarau mathematics and tauanga statistics in Aotearoa New Zealand: Advice on refreshing the English-medium Mathematics and Statistics learning area of the New Zealand Curriculum. Royal Society Te Apārangi. Retrieved from https://www.royalsociety.org.nz/assets/Pangarau-Mathematics-and-Tauanga-Statistics-in-Aotearoa-New-Zealand-Digital.pdf
- [1] Parsons, S., & Bynner, J. (2005). Does numeracy matter more?. National Research and Development Centre for Adult Literacy and Numeracy
- [1] Expert Advisory Panel. (2021). Pāngarau mathematics and tauanga statistics in Aotearoa New Zealand: Advice on refreshing the English-medium Mathematics and Statistics learning area of the New Zealand Curriculum. Royal Society Te Apārangi. Retrieved from https://www.royalsociety.org.nz/assets/Pangarau-Mathematics-and-Tauanga-Statistics-in-Aotearoa-New-Zealand-Digital.pdf
- [1] Ministry of Education. (2022). What your child learns at early learning services. Retrieved from https://parents.education.govt.nz/early-learning/learning-at-an-ece-service/what-your-child-learns-at-ece/#whatwilltheylearn
- The Education Hub. (2020). An introduction to supporting early maths in early childhood education. Retrieved from https://theeducationhub.org.nz/an-introduction-to-supporting-early-maths-in-ece/#:~:text=They%20explore%20maths%20on%20their,arithmetic%20with%20groups%20of%20objects.
- [1] Education Review Office. (2016). Early mathematics: A guide for improving teaching and learning. New Zealand Government. Retrieved from https://ero.govt.nz/our-research/early-mathematics-a-guide-for-improving-teaching-and-learning
- [1] Ell, F., & Darragh, L. (n.d.). Teaching and learning mathematics at primary school. Retrieved from The Education Hub: https://theeducationhub.org.nz/teaching-and-learning-mathematics-at-primary-school/
- [1] Education Review Office. (2016). Early Mathematics: A guide for improving teaching and learning. New Zealand Government. Retrieved from https://ero.govt.nz/our-research/early-mathematics-a-guide-for-improving-teaching-and-learning
- Ell, F., & Darragh, L. (n.d.). Teaching and learning mathematics at primary school. Retrieved from The Education Hub: https://theeducationhub.org.nz/teaching-and-learning-mathematics-at-primary-school/
- [1] Holenstein, M., Bruckmaier, G. & Grob, A. (2021). Transfer effects of mathematical literacy: an integrative longitudinal study. European Journal of Psychology of Education, 36(9), 799–825. https://doi.org/10.1007/s10212-020-00491-4
- [1] Mohyuddin, R. G., & Khalil, U. (2016). Misconceptions of Students in Learning Mathematics at Primary Level. Bulletin of Education and Research, 38(1), 133-162.Fujii, T. (2020).
- Misconceptions and alternative conceptions in mathematics education. Encyclopedia of mathematics education, 625-627.
- [1] Gibbs, B., White, A., & McDowall, S. (2022). Developing a common practice model for literacy & communciation and maths: An overview of the literature. New Zealand Council for Educational Research.
- [1] Ministry of Education. (2022). Which angle is a right angle? Year 5 students’ strengths and weaknesses on mathematics questions. Retrieved from https://www.educationcounts.govt.nz/__data/assets/pdf_file/0003/213186/Which-angle-is-a-right-angle-Year-5-students-strengths-and-weaknesses-on-mathematics-questions.pdf
- [1] Ministry of Education. (2022). Which angle is a right angle? Year 5 students’ strengths and weaknesses on mathematics questions. Retrieved from https://www.educationcounts.govt.nz/__data/assets/pdf_file/0003/213186/Which-angle-is-a-right-angle-Year-5-students-strengths-and-weaknesses-on-mathematics-questions.pdf
- [1] OECD. (2023). PISA 2022 results: The state of learning and equality in education. Retrieved from https://read.oecd-ilibrary.org/view/?ref=1235_1235421-gumq51fbgo&title=PISA-2022-Results-Volume-I
- [1] Ministry of Education. (2023). PISA 2022 Mathematics Achievement and Experiences of 15-year-olds, by Emma Medina. Retrieved from https://www.educationcounts.govt.nz/__data/assets/pdf_file/0005/224609/PISA-2022_Mathematics-Achievement-and-Experiences-Report.pdf
- OECD. (2023). PISA 2022 results: The state of learning and equality in education. Retrieved from https://read.oecd-ilibrary.org/view/?ref=1235_1235421-gumq51fbgo&title=PISA-2022-Results-Volume-I
- OECD. (2023). PISA 2022 results. Retrieved from https://www.oecd.org/publication/pisa-2022-results/
- [1] National Monitoring Study of Student Achievement. (2022). Achievement in mathematics and statistics at year 4 and year 8: Findings from the 2022 National Monitoring Study of Student Achievement (NMSSA). Retrieved from https://nmssa-production.s3.amazonaws.com/documents/A3_NMSSA_2022_Achievement_Summary_Mathematics.pdf
- Ministry of Education. (2018). Achievement and progress in mathematics, reading and writing in primary schooling: Analysis of e-asTTle assessment data, 2011 to 2016. Retrieved from https://www.educationcounts.govt.nz/__data/assets/pdf_file/0019/185023/20171213-Achievement-and-Progress-in-mathematics-reading-and-writing.pdf
- [1] National Monitoring Study of Student Achievement. (2022). Achievement in mathematics and statistics at year 4 and year 8: Findings from the 2022 National Monitoring Study of Student Achievement (NMSSA). Retrieved from https://nmssa-production.s3.amazonaws.com/documents/A3_NMSSA_2022_Achievement_Summary_Mathematics.pdf
- [1] National Monitoring Study of Student Achievement. (2022). Achievement in mathematics and statistics at year 4 and year 8: Findings from the 2022 National Monitoring Study of Student Achievement (NMSSA). Retrieved from https://nmssa-production.s3.amazonaws.com/documents/A3_NMSSA_2022_Achievement_Summary_Mathematics.pdf
- [1] Medina, E. (2023). PISA 2022: Mathematics achievement and experiences of 15-year-olds. Retrieved from https://www.educationcounts.govt.nz/__data/assets/pdf_file/0005/224609/PISA-2022_Mathematics-Achievement-and-Experiences-Report.pdf
- [1] Education Review Office. (2022). Ongoing research on new teachers (forthcoming publication).
- [1] National Monitoring Study of Student Achievement. (2023). Mathematics and statistics: contextual findings 2022. Retrieved from https://nmssa-production.s3.amazonaws.com/documents/NMSSA_2022_Mathematics_Contextual_Findings.pdf
- [1] Expert Advisory Panel. (2021). Pāngarau mathematics and tauanga statistics in Aotearoa New Zealand: Advice on refreshing the English-medium Mathematics and Statistics learning area of the New Zealand Curriculum. Royal Society Te Apārangi. Retrieved from https://www.royalsociety.org.nz/assets/Pangarau-Mathematics-and-Tauanga-Statistics-in-Aotearoa-New-Zealand-Digital.pdf
- [1] Anderson, R., Boaler, J., & Dieckmann, J. (2018). Achieving Elusive Teacher Change through Challenging Myths about Learning: A Blended Approach. Education Sciences, 8(3), 98. MDPI AG. Retrieved from http://dx.doi.org/10.3390/educsci8030098
- [1] Anderson, R., Boaler, J., & Dieckmann, J. (2018). Achieving Elusive Teacher Change through Challenging Myths about Learning: A Blended Approach. Education Sciences, 8(3), 98. MDPI AG. Retrieved from http://dx.doi.org/10.3390/educsci8030098
- [1] Expert Advisory Panel. (2021). Pāngarau mathematics and tauanga statistics in Aotearoa New Zealand: Advice on refreshing the English-medium Mathematics and Statistics learning area of the New Zealand Curriculum. Royal Society Te Apārangi. Retrieved from https://www.royalsociety.org.nz/assets/Pangarau-Mathematics-and-Tauanga-Statistics-in-Aotearoa-New-Zealand-Digital.pdf
- [1] Anthony, G., & Walshaw, M. (2007). Effective Pedagogy in Mathematics/Pāngarau. Ministry of Education.
- [1] Ministry of Education. (n.d.). Local curriculum: Designing rich opportunities and coherent pathways for all students. Retrieved from https://nzcurriculum.tki.org.nz/Strengthening-local-curriculum/Leading-local-curriculum-guide-series/Local-curriculum
- [1] Anthony, G., & Walshaw, M. (2007). Effective Pedagogy in Mathematics/Pāngarau. Ministry of Education.
- Mohyuddin, R. G., & Khalil, U. (2016). Misconceptions of Students in Learning Mathematics at Primary Level. Bulletin of Education and Research, 38(1), 133-162.
- Fujii, T. (2020). Misconceptions and alternative conceptions in mathematics education. Encyclopedia of mathematics education, 625-627.
- Anderson, D. and Pritchard, R. (2010). Bridging the gap: Challenging conceptions of fractions and decimals. In Teaching Primary School Mathematics and Statistics, Eds. R. Averill & R. Harvey. NZCER Press: Wellington.
- [1] Clark, A., Henderson, P., & Gifford, S. (2020). Improving mathematics in the early years and key stage 1. Education Endowment Foundation. Retrieved from https://d2tic4wvo1iusb.cloudfront.net/production/eef-guidance-reports/early-maths/EEF_Maths_EY_KS1_Guidance_Report.pdf?v=1699919581
- [1] Expert Advisory Panel. (2021). Pāngarau mathematics and tauanga statistics in Aotearoa New Zealand: Advice on refreshing the English-medium Mathematics and Statistics learning area of the New Zealand Curriculum. Royal Society Te Apārangi. Retrieved from https://www.royalsociety.org.nz/assets/Pangarau-Mathematics-and-Tauanga-Statistics-in-Aotearoa-New-Zealand-Digital.pdf
- [1] Clark, A., Henderson, P., & Gifford, S. (2020). Improving mathematics in the early years and key stage 1. Education Endowment Foundation. Retrieved from https://d2tic4wvo1iusb.cloudfront.net/production/eef-guidance-reports/early-maths/EEF_Maths_EY_KS1_Guidance_Report.pdf?v=1699919581
- Dweck, C. S. (2006). Mindset: The new psychology of success. Random house.
- [1] Ministry of Education. (n.d.). Local curriculum: Designing rich opportunities and coherent pathways for all students. Retrieved from https://nzcurriculum.tki.org.nz/Strengthening-local-curriculum/Leading-local-curriculum-guide-series/Local-curriculum
- [1] Clark, A., Henderson, P., & Gifford, S. (2020). Improving mathematics in the early years and key stage 1. Education Endowment Foundation. Retrieved from https://d2tic4wvo1iusb.cloudfront.net/production/eef-guidance-reports/early-maths/EEF_Maths_EY_KS1_Guidance_Report.pdf?v=1699919581
- [1] Clark, A., Henderson, P., & Gifford, S. (2020). Improving mathematics in the early years and key stage 1. Education Endowment Foundation. Retrieved from https://d2tic4wvo1iusb.cloudfront.net/production/eef-guidance-reports/early-maths/EEF_Maths_EY_KS1_Guidance_Report.pdf?v=1699919581
- [1] Ministry of Education. (2023). A model of educational leadership. Retrieved from https://www.educationalleaders.govt.nz/Leadership-development/Key-leadership-documents/Kiwi-leadership-for-principals/A-model-of-educational-leadership
- [1] Hattie, J. (2016, July). Mindframes and Maximizers. 3rd Annual Visible Learning Conference held in Washington, DC
- Donohoo, J., Hattie, J., & Eells, R. (2018). The power of collective efficacy. Educational Leadership, 75(6), 40-44.
- [1] Ministry of Education. (n.d.). Ka Hikitia – Ka Hāpaitia. Retrieved from https://www.education.govt.nz/our-work/overall-strategies-and-policies/ka-hikitia-ka-hapaitia/
- Ministry of Education. (2023). Action plan for Pacific education 2020-2030: 2023 refresh. Retrieved from https://www.education.govt.nz/our-work/overall-strategies-and-policies/action-plan-for-pacific-education/
- [1] Kaskens, J., Segers, E., Goei, S. L., van Luit, J. E., & Verhoeven, L. (2020). Impact of Children’s math self-concept, math self-efficacy, math anxiety, and teacher competencies on math development. Teaching and teacher education, 94, 103096.
- Beswick, K. (2019). The role of knowledge and beliefs in helping students to progress their mathematical understanding. J Math Teacher Educ 22, 125–128
- [1] Flint, A., Garrett, L., McDonald, L., Rubie-Davies, C. M., & Watson, P. W. (2018). December 10). Viewing students consistently: how stable are teachers’ expectations? Educational Research and Evaluation, 24(3-5), 221-240.
- Philipp, R. A. (2007). Mathematics teachers' beliefs and affect. In F. K. Lester (ed.), Second handbook of research on mathematics teaching and learning (pp. 257–315). Charlotte: NCTM/Information Age Publishing
- Rubie-Davies, C. M., & Peterson, E. R. (2016). Relations between teachers’ over - and underestimation, and students' beliefs for Māori & Pākeha students.. Contemporary Educational Psychology, 47, 72-83.
- Hollenstein, L., Rubie-Davies, C. M., & Brühwiler, C. (2023). Teacher expectations and their relations with primary school students’ achievement, self-concept, and anxiety in mathematics. Social Psychology of Education, 1-20.
- [1] Kaskens, J., Segers, E., Goei, S. L., van Luit, J. E., & Verhoeven, L. (2020). Impact of Children’s math self-concept, math self-efficacy, math anxiety, and teacher competencies on math development. Teaching and teacher education, 94, 103096.
- Clark, A., Henderson, P., & Gifford, S. (2020). Improving mathematics in the early years and key stage 1. Education Endowment Foundation. Retrieved from https://d2tic4wvo1iusb.cloudfront.net/production/eef-guidance-reports/early-maths/EEF_Maths_EY_KS1_Guidance_Report.pdf?v=1699919581
- [1] Clark, A., Henderson, P., & Gifford, S. (2020). Improving mathematics in the early years and key stage 1. Education Endowment Foundation. Retrieved from https://d2tic4wvo1iusb.cloudfront.net/production/eef-guidance-reports/early-maths/EEF_Maths_EY_KS1_Guidance_Report.pdf?v=1699919581
- [1] Clark, A., Henderson, P., & Gifford, S. (2020). Improving mathematics in the early years and key stage 1. Education Endowment Foundation. Retrieved from https://d2tic4wvo1iusb.cloudfront.net/production/eef-guidance-reports/early-maths/EEF_Maths_EY_KS1_Guidance_Report.pdf?v=1699919581
- [1] Anthony, G., & Walshaw, M. (2007). Effective pedagogy in mathematics/pāngarau: Best Evidence Synthesis Iteration [BES]. Ministry of Education.
- [1] National Council of Teachers of Mathematics. (2023). Procedural Fluency in Mathematics. Retrieved from https://www.nctm.org/Standards-and-Positions/Position-Statements/Procedural-Fluency-in-Mathematics/
- [1] Doabler, C. T., Cary, M. S., Jungjohann, K., Clarke, B., Fien, H., Baker, S., & Chard, D. (2012). Enhancing core mathematics instruction for students at risk for mathematics disabilities. Teaching Exceptional Children, 44(4), 48-57.
- [1] Wang, A. H., Firmender, J. M., Power, J. R., & Byrnes, J. P. (2016). Understanding the Program Effectiveness of Early Mathematics Interventions for Prekindergarten and Kindergarten Environments: A Meta-Analytic Review. Early Education and Development, 27(5), 692–713. https://doi.org/10.1080/10409289.2016.1116343
- [1] Wright, J. Intervention Central. (n.d.). Math Problem-Solving: Combining Cognitive & Metacognitive Strategies. Retrieved from https://www.interventioncentral.org/academic-interventions/math/math-problem-solving-combining-cognitive-metacognitive-strategies
- [1] Clark, A., Henderson, P., & Gifford, S. (2020). Improving mathematics in the early years and key stage 1. Education Endowment Foundation. Retrieved from https://d2tic4wvo1iusb.cloudfront.net/production/eef-guidance-reports/early-maths/EEF_Maths_EY_KS1_Guidance_Report.pdf?v=1699919581
- [1] Expert Advisory Panel. (2021). Pāngarau mathematics and tauanga statistics in Aotearoa New Zealand: Advice on refreshing the English-medium Mathematics and Statistics learning area of the New Zealand Curriculum. Royal Society Te Apārangi. Retrieved from https://www.royalsociety.org.nz/assets/Pangarau-Mathematics-and-Tauanga-Statistics-in-Aotearoa-New-Zealand-Digital.pdf
- [1] O'Neill, S., Gillic, C., & Kingston, M. (2023). Pedagogical strategies, approaches and methodologies to support numeracy in early childhood A review of the literature.
- [1] National Council of Teachers of Mathematics. (2023). Procedural Fluency Reasoning and Decision-Making, Not Rote Application of Procedures Position. Retrieved from https://www.nctm.org/Standards-and-Positions/Position-Statements/Procedural-Fluency-in-Mathematics/
- [1] NRICH team. (2019). Low Threshold High Ceiling - an Introduction. Retrieved from https://nzcurriculum.tki.org.nz/content/download/169510/1250686/file/CO3072_Maths_Principals_011-web.pdf
- Sullivan, P., Bragg, L. A. (Ed.), Cheeseman, J., Michels, D., Mornane, A., Clarke, D., Middleton, J., & Roche, A. (2011). Challenging mathematics tasks: What they are and how to use them. 33-46.
- Grootenboer, P. (2009). Rich mathematical tasks in the Maths in the Kimberley (MITK) Project. 696-699.
- [1] Ministry of Education. (2022). Leading mathematics teaching and learning in years 1-8: What principals need to know and be able to do. file:///C:/Users/ruthp/AppData/Local/Temp/MicrosoftEdgeDownloads/4761cd9b-f999-4f7c-9b4e-896b2751195e/CO3072_Maths_Principals_011-web.pdf
- [1] NRICH team. (2019). Low Threshold High Ceiling - an Introduction. Retrieved from https://nrich.maths.org/10345
- [1] Gervasoni, A., & Lindenskov, L. (2011). Students with ‘special rights’ for mathematics education. Mapping equity and quality in mathematics education, 307-323.
- [1] Anthony, G., & Walshaw, M. (2007). Effective Pedagogy in Mathematics/Pāngarau. Ministry of Education.
- Beyers, J. (2011). Student dispositions with respect to mathematics: What current literature says. Motivation and disposition: Pathways to learning mathematics, 69-79.
- OECD. (2013). Mathematics self-beliefs and participation in mathematics-related activities. PISA2012-Vol3-Chap4.pdf (oecd.org)
- OECD. (2013). PISA 2012 Results: Ready to Learn (Volume III): Students' Engagement, Drive and Self-Beliefs. Paris: PISA, OECD Publishing. Retrieved from https://doi.org/10.1787/19963777
- OECD. (2016). Opportunity to Learn and Students' Attitudes Towards Mathematics. In Equations and Inequalities: Making Mathematics Accessible to All. Paris: OECD Publishing. doi: https://doi.org/10.1787/9789264258495-7-en
- [1] Mielicki, M. K., Schiller, L. K., Fitzsimmons, C. J., Scheibe, D., & Thompson, C. A. (2022). Perceptions of ease and difficulty, but not growth mindset, relate to specific math attitudes. British Journal of Educational Psychology, 92(2), 707-729.
- [1] NRICH team. (2019). Low Threshold High Ceiling - an Introduction. Retrieved from https://nrich.maths.org/10345
- Livy, S., Muir, T., & Sullivan, P. (2018). Challenging tasks lead to productive struggle!. Australian Primary Mathematics Classroom, 23(1), 19-24.
- [1] Hattie, J. (2016, July). Mindframes and Maximizers. 3rd Annual Visible Learning Conference held in Washington, DC
- [1] Dweck, C. S. (2006). Mindset: The new psychology of success. Random house.
- [1] Sullivan, P., Cheeseman, J., Michels, D., Mornane, A., Clarke, D., Roche, A., & Middleton, J. (2011). Challenging mathematics tasks: What they are and how to use them. Maths is multi-dimensional, 33-46.
- Sullivan, P. (2017). Challenging mathematics tasks: What they are and how to use them.
- [1] Clark, A., Henderson, P., & Gifford, S. (2020). Improving mathematics in the early years and key stage 1. Education Endowment Foundation. Retrieved from https://d2tic4wvo1iusb.cloudfront.net/production/eef-guidance-reports/early-maths/EEF_Maths_EY_KS1_Guidance_Report.pdf?v=1699919581
- [1] Clark, A., Henderson, P., & Gifford, S. (2020). Improving mathematics in the early years and key stage 1. Education Endowment Foundation. Retrieved from https://d2tic4wvo1iusb.cloudfront.net/production/eef-guidance-reports/early-maths/EEF_Maths_EY_KS1_Guidance_Report.pdf?v=1699919581
- [1] Education Review Office. (2022). A practical guide for teachers: What quality teacher aide practice looks like. Retrieved from https://ero.govt.nz/our-research/a-practical-guide-for-teachers-what-quality-teacher-aide-practice-looks-like
- [1] Ministry of Education. (n.d.). Accelerating learning in mathematics fact sheet. Te Kete Ipurangi.
- [1] Ministry of Education. (2012). Resource 8: Creating purposeful independent activitiesl. Retrieved from https://nzmaths.co.nz/sites/default/files/images/ALiM_Resource08.pdf
- [1] nzmaths. (n.d.). ALiM resources. Retrieved from Te Kete Ipurangi: https://nzmaths.co.nz/alim-resources
- [1] Diezmann, C., & Watters, J., 1997, as cited in Anthony, G., & Walshaw, M. (2007). Effective pedagogy in mathematics/pāngarau: Best Evidence Synthesis Iteration [BES]. Ministry of Education.
- [1] Kusmaryono, I. (2014). The importance of mathematical power in mathematics learning. In International Conference on Mathematics, Science, and Education (Vol. 2014, pp. 35-40).
- [1] Sullivan, P., Bragg, L. A. (Ed.), Cheeseman, J., Michels, D., Mornane, A., Clarke, D., Middleton, J., & Roche, A. (2011). Challenging mathematics tasks: What they are and how to use them. 33-46.
- [1] Diezmann, C., & Watters, J., 1997, as cited in Anthony, G., & Walshaw, M. (2007). Effective pedagogy in mathematics/pāngarau: Best Evidence Synthesis Iteration [BES]. Ministry of Education.
- Mendes, I. A., & da Silva, C. A. (2018). Problematization and research as a method of teaching mathematics. International Electronic Journal of Mathematics Education, 13(2), 41-55. Retrieved from https://www.iejme.com/download/problematization-and-research-as-a-method-of-teaching-mathematics.pdf
- Mathematics Hub. (n.d.). Mathematics investigation. Retrieved from https://www.mathematicshub.edu.au/plan-teach-and-assess/teaching/teaching-strategies/mathematics-investigation/
- [1] Clark, A., Henderson, P., & Gifford, S. (2020). Improving mathematics in the early years and key stage 1. Education Endowment Foundation. Retrieved from https://d2tic4wvo1iusb.cloudfront.net/production/eef-guidance-reports/early-maths/EEF_Maths_EY_KS1_Guidance_Report.pdf?v=1699919581
- Mueller, M., Yankelewitz, D., & Maher, C. (2014). Teachers promoting student mathematical reasoning. Investigations in Mathematics Learning, 7(2). Retrieved from https://files.eric.ed.gov/fulltext/EJ1052941.pdf
- [1] Clark, A., Henderson, P., & Gifford, S. (2020). Improving mathematics in the early years and key stage 1. Education Endowment Foundation. Retrieved from https://d2tic4wvo1iusb.cloudfront.net/production/eef-guidance-reports/early-maths/EEF_Maths_EY_KS1_Guidance_Report.pdf?v=1699919581
- [1] Anthony, G., & Walshaw, M. (2009). Effective pedagogy in mathematics. International Academy of Education, 19, 136. Retrieved from https://nzmaths.co.nz/sites/default/files/images/EdPractices_19.pdf
- [1] Clark, A., Henderson, P., & Gifford, S. (2020). Improving mathematics in the early years and key stage 1. Education Endowment Foundation. Retrieved from https://d2tic4wvo1iusb.cloudfront.net/production/eef-guidance-reports/early-maths/EEF_Maths_EY_KS1_Guidance_Report.pdf?v=1699919581
- [1] Clements, D. H., & Sarama, J. (2016). Math, Science, and Technology in the Early Grades. The Future of Children, 26(2), 75–94. Retrieved from http://www.jstor.org/stable/43940582
- [1] Clark, A., Henderson, P., & Gifford, S. (2020). Improving mathematics in the early years and key stage 1. Education Endowment Foundation. Retrieved from https://d2tic4wvo1iusb.cloudfront.net/production/eef-guidance-reports/early-maths/EEF_Maths_EY_KS1_Guidance_Report.pdf?v=1699919581
- [1] OECD. (2016). Opportunity to Learn and Students' Attitudes Towards Mathematics. In Equations and Inequalities: Making Mathematics Accessible to All. Paris: OECD Publishing. doi:https://doi.org/10.1787/9789264258495-7-en
- Anthony, G., & Walshaw, M. (2007). Effective pedagogy in mathematics/pāngarau: Best Evidence Synthesis Iteration [BES]. Ministry of Education.
- Bonne, L. (2016). New Zealand Students’ mathematics-related beliefs and attitudes: recent evidence. N.Z.J. Educ. Stud. 51, 69–82. doi: 10.1007/s40841-016-0035-2
- [1] Stein, C. A. (2007). Let's talk: Promoting mathematical discourse in the classroom. The Mathematics Teacher, 101(4), 285-289.
- Goos, M., & Kaya, S. (2020). Understanding and promoting students’ mathematical thinking: a review of research published in ESM. Educational Studies in Mathematics, 103(1), 7-25.
- Anthony, G., & Walshaw, M. (2007). Effective pedagogy in mathematics/pāngarau: Best Evidence Synthesis Iteration [BES]. Ministry of Education.
- [1] Anthony, G., & Walshaw, M. (2007). Effective pedagogy in mathematics/pāngarau: Best Evidence Synthesis Iteration [BES]. Ministry of Education.
- Clark, A., Henderson, P., & Gifford, S. (2020). Improving mathematics in the early years and key stage 1. Education Endowment Foundation. Retrieved from https://d2tic4wvo1iusb.cloudfront.net/production/eef-guidance-reports/early-maths/EEF_Maths_EY_KS1_Guidance_Report.pdf?v=1699919581
- [1] Stein, C. A. (2007). Let's talk: Promoting mathematical discourse in the classroom. The Mathematics Teacher, 101(4), 285-289.
- Way, J. & Bobis, J. (2017). The Literacy of Mathematics. PETAA – Primary English Teaching Association Australia, 208, 1-12.
- [1] Anthony, G & Walshaw, M. (2009). Effective Pedagogy in Mathematics/Pāngarau BES
- Nzmaths (n.d.). Foster a supportive learning environment.
- Retrieved from: https://nzmaths.co.nz/foster-supportive-learning-environment
- [1] Anderson, D., Averill, R., Te Maro, P., Taiwhati, M., & Higgins, J. (2010). Knowing each other as students: Māori students learning mathematics. Delving into diversity: An international exploration of issues of diversity in education, 45-56.
- [1] Anthony, G., & Walshaw, M. (2007). Creating opportunities for learning with mathematical tasks. Set: Research Information for Teachers(1), 7-11. doi:10.18296/set.0547
- [1] Clark, A., Henderson, P., & Gifford, S. (2020). Improving mathematics in the early years and key stage 1. Education Endowment Foundation. Retrieved from https://d2tic4wvo1iusb.cloudfront.net/production/eef-guidance-reports/early-maths/EEF_Maths_EY_KS1_Guidance_Report.pdf?v=1699919581
- [1] Charles, R. I., & Carmel, C. A. (2005). Big ideas and understandings as the foundation for elementary and middle school mathematics. Journal of Mathematics Education, 7(3), 9-24.
- McDowell, S., & Hipkins, R. (n.d.). Cultural integration: what is happening in New Zealand schools? New Zealand Council for Educational Research. Retrieved from https://www.nzcer.org.nz/system/files/Curriculum%20Integration%202018-2019.pdf
- [1] Anthony, G., & Walshaw, M. (2007). Creating opportunities for learning with mathematical tasks. Set: Research Information for Teachers(1), 7-11. doi:10.18296/set.0547
- [1] De Holton, D., Ahmed, A., Williams, H., & Hill, C. (2001). On the importance of mathematical play. International Journal of Mathematical Education in Science and Technology, 32(3), 401-415.
- Hanline, M. F., Milton, S., & Phelps, P. C. (2010). The relationship between preschool block play and reading and maths abilities in early elementary school: A longitudinal study of children with and without disabilities. Early Child Development and Care, 180(8), 1005-1017.
- [1] Clark, A., Henderson, P., & Gifford, S. (2020). Improving mathematics in the early years and key stage 1. Education Endowment Foundation. Retrieved from https://d2tic4wvo1iusb.cloudfront.net/production/eef-guidance-reports/early-maths/EEF_Maths_EY_KS1_Guidance_Report.pdf?v=1699919581
- [1] Ministry of Education. (2022). Leading mathematics teaching and learning in years 1-8: What principals need to know and be able to do. https://nzcurriculum.tki.org.nz/content/download/169510/1250686/file/CO3072_Maths_Principals_011-web.pdf
- [1] Education Review Office. (2023). Education For All Our Children: Embracing Diverse Ethnicities. Retrieved from https://ero.govt.nz/our-research/education-for-all-our-children-embracing-diverse-ethnicities
- [1] OECD. (2016). Equations and Inequalities: Making Mathematics Accessible to All. Retrieved from https://www.oecd-ilibrary.org/education/equations-and-inequalities_9789264258495-en
- [1] Education Council. (n.d.). Our code our standards: code of professional responsibility and standards for the teaching profession. Retrieved from https://teachingcouncil.nz/assets/Files/Code-and-Standards/Our-Code-Our-Standards-Nga-Tikanga-Matatika-Nga-Paerewa.pdf
- Ministry of Education. (2015). The New Zealand Curriculum for English-medium teaching and learning in years 1-13. Wellington.
- Ministry of Education. (n.d.). Ka Hikitia – Ka Hāpaitia. Retrieved from https://www.education.govt.nz/our-work/overall-strategies-and-policies/ka-hikitia-ka-hapaitia/
- Ministry of Education. (2022). Literacy & communication and maths strategy. Retrieved from https://assets.education.govt.nz/public/Documents/Ministry/Changes-in-education/ELS-0778-Maths-and-Literacy-Strategies-Doc_web.pdf
- [1] Averill, R., Anderson, D., Easton, H., Te Maro, P., Smith, D., & Hynds, A. (2009). Culturally Responsive Teaching of Mathematics: Three Models from Linked Studies. Journal for Research in Mathematics Education, 40(2), 157-186. Retrieved from https://www.jstor.org/stable/40539330
- [1] Hunter, Jodie. (n.d.). Ambitious mathematics for young Pacific students: Dr Jodie Hunter demonstrates algebraic thinking for tivaevae. Retrieved from Education Counts: https://www.educationcounts.govt.nz/topics/bes/ambitious-mathematics-for-young-pacific-students
- Barnes, G. (2023, June 3). My Tūrangawaewae. Retrieved from https://instructionalseries.tki.org.nz/Instructional-Series/School-Journal/School-Journal-Level-2-June-2023/My-Turangawaewae
- [1] Te Poutāhū. (n.d.). Pattern Makers. Retrieved from https://newzealandcurriculum.tahurangi.education.govt.nz/pattern-makers/5637186629.p
- [1] Hunter, Jodie. (n.d.). Ambitious mathematics for young Pacific students: Dr Jodie Hunter demonstrates algebraic thinking for tivaevae. Retrieved from Education Counts: https://www.educationcounts.govt.nz/topics/bes/ambitious-mathematics-for-young-pacific-students
- Barnes, G. (2023, June 3). My Tūrangawaewae. Retrieved from https://instructionalseries.tki.org.nz/Instructional-Series/School-Journal/School-Journal-Level-2-June-2023/My-Turangawaewae
- [1] Education Review Office. (2015). Educationally powerful connections with parents and whānau. Retrieved from https://ero.govt.nz/our-research/educationally-powerful-connections-with-parents-and-whanau
- Ministry of Education (n.d). Partnering with parents, whānau, and communities. Retrieved from https://inclusive.tki.org.nz/guides/partnering-with-parents-whanau-and-communities/
- The Education Hub. (2020). What is parent partnership? Retrieved from https://theeducationhub.org.nz/what-is-parent-partnership/
- Anthony, G., & Walshaw, M. (2007). Effective pedagogy in mathematics/pāngarau: Best Evidence Synthesis Iteration [BES]. Ministry of Education.
- [1] Stanford Graduate School of Education. (n.d.). Parents’ beliefs about math change their children’s achievement. Retrieved from youcubed: https://www.youcubed.org/evidence/parents-beliefs-math-change-childrens-achievement/
- [1] O'Neill, S., Gillic, C., & Kingston, M. (2023). Pedagogical strategies, approaches and methodologies to support numeracy in early childhood A review of the literature.
- [1] Stanford Graduate School of Education. (n.d.). Parents’ beliefs about math change their children’s achievement. Retrieved from youcubed: https://www.youcubed.org/evidence/parents-beliefs-math-change-childrens-achievement/
- [1] Farr, S. (2015). The role of parents in children's attitudes towards mathematics. Retrieved from https://researchcommons.waikato.ac.nz/bitstream/handle/10289/10007/thesis.pdf?sequence=3&isAllowed=y
- [1] nzmaths. (n.d.). Guiding beliefs. Retrieved from Te Kete Ipurangi: https://nzmaths.co.nz/guiding-beliefs
- [1] Papadopoulos, I. (2017). Opening inquiry mathematics to parents: Can they be engaged as teachers’ partners in mathematical work? Journal of Pedagogical Research, 1(1), 1-20.


